Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Khẳng định nào sau đây là đúng?
A. Q cách đều ba đỉnh của ∆NPR;
B. Q cách đều ba cạnh của ∆NPR;
C. MN, PQ và RQ đồng quy.
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C
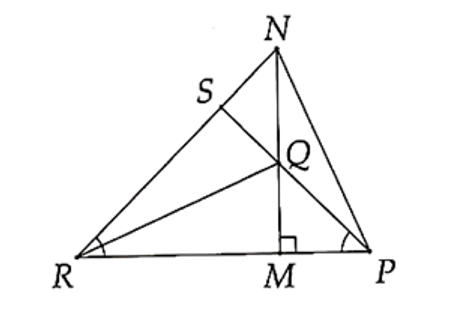
Gọi S là giao điểm PQ và RN.
ΔMPQ vuông tại M có MQ = MP nên là tam giác vuông cân tại M, do đó
Suy ra (đối đỉnh)
Tương tự, ΔMNR vuông cân tại M có
Trong ΔNSQ có: và
Do đó nên QS ⊥ NS hay PS ⊥ NR.
Trong ΔNPR có các đường cao PS và NM cắt nhau tại Q.
Suy ra Q là trực tâm ΔNPR. Do đó Q không cách đều ba cạnh, ba đỉnh của ΔPNR.
Vậy MN, PQ và RQ đồng quy, ta chọn phương án C.
Cho tam giác ABC vuông tại A có BD là đường phân giác. Trên cạnh BC lấy điểm E sao cho BA = BE. Vẽ CH ⊥ DB. Cho các khẳng định sau:
(I) Ba đường thẳng BA, DE, CH đồng quy;
(II) Đường thẳng DE đi qua giao điểm của AB và CH;
(III) DE ⊥ BC.
Có bao nhiêu khẳng định sai?
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, tia Oy lấy điểm B sao cho OA = OB. Kẻ AC ⊥ Oy, BD ⊥ Ox (C ∈ Oy, D ∈ Ox). Đường thẳng vuông góc với Ox tại A và đường thẳng vuông góc với Oy tại B cắt nhau tại M. Khẳng định nào sau đây là sai?
Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM. Khẳng định nào sau đây là sai?
Cho tam giác ABC cân tại A có đường phân giác AH (H ∈ BC). Đường trung trực của cạnh AB cắt đường AH tại O. Trên các cạnh AB và AC lấy các điểm E và F sao cho: AE + AF = AB. Hỏi E và F ở vị trí nào để O là trung điểm của EF?
Cho tam giác ABC cân ở A, đường phân giác AK. Các đường trung trực của AB và AC cắt nhau tại O. Kéo dài CO cắt AB ở D, kéo dài BO cắt AC ở E.
Khẳng định nào sau đây là đúng?
Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM. Cho các phát biểu sau:
(I) BM là đường trung trực của AD;
(II) AK, DH, BM đồng quy tại một điểm;
(III) AK // BC.
Khẳng định nào sau đây là đúng?
Cho ∆ABC vuông ở A, gọi D là giao điểm của hai đường trung trực của hai cạnh AB và AC. Khẳng định nào dưới đây là sai?
Cho tam giác ABC cân tại A có M là trung điểm của BC. Kẻ đường thẳng d vuông góc AB tại B, kẻ đường thẳng d’ vuông góc với AC tại C, hai đường thẳng d và d’ giao nhau giao tại D. Cho các khẳng định sau:
(I) A nằm trên đường trung trực của BC;
(II) Ba điểm A, M, D thẳng hàng.
Khẳng định nào sau đây là đúng nhất?
Cho ba tam giác cân phân biệt ABC, DBC và EBC có chung đáy BC. Vị trí của ba điểm A, D và E là?
