Từ đoạn 10 (dòng 51-59), ta có thể rút ra kết luận nào sau đây?
A. Sản phẩm chủ lực hiện nay của Thực phẩm lý tưởng là nấm chế biến.
B. Các siêu thị lớn chưa chấp nhận kinh doanh sản phẩm nấm chế biến.
C. Nấm chế biến là sản phẩm có hàm lượng khoa học công nghệ cao.
 Giải bởi Vietjack
Giải bởi Vietjack
A. Sản phẩm chủ lực hiện nay của Thực phẩm lý tưởng là nấm chế biến. → Sai, thông tin tại dòng 52-53.
B. Các siêu thị lớn chưa chấp nhận kinh doanh sản phẩm nấm chế biến. → Sai, thông tin tại dòng 52.
C. Nấm chế biến là sản phẩm có hàm lượng khoa học công nghệ cao. → Đúng, thông tin tại dòng 56-57.
D. Công ty Thực phẩm lý tưởng đang được hưởng ưu đãi thuế cho doanh nghiệp khoa học công nghệ. → Sai, tỉ trọng doanh thu từ sản phẩm công nghệ chưa đủ 30% nên chưa được hưởng ưu đãi thuế.
Chọn C
Một vật chuyển động trong 4 giờ với vận tốc v(km/h) phụ thuộc thời gian t(h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2;9) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 4 giờ đó.
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1;0;1), B(1;0;−3) và điểm D có hoành độ âm. Mặt phẳng (ABCD) đi qua gốc tọa độ O. Khi đó đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có phương trình
Gọi S là tập hợp các số tự nhiên có 6 chữ số được lập từ tập A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
Có bao nhiêu giá trị nguyên dương của m để bất phương trình nghiệm đúng với mọi x ∈ (0;1)?
Cho hàm số , biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng
Từ thông tin tại đoạn cuối (dòng 43-53), nhận định nào sau đây là chính xác?
Cho hàm số y = f(x) có đạo hàm trên ℝ và có bảng biến thiên như sau:
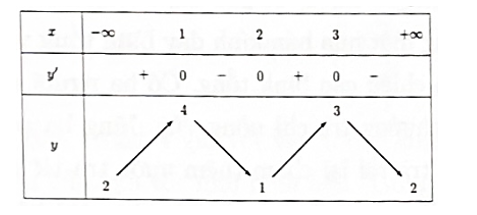
Tổng các giá trị nguyên của tham số m để phương trình có đúng hai nghiệm phân biệt bằng
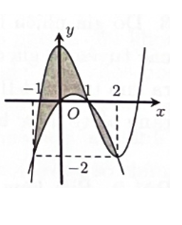
Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
Trong hệ trục tọa độ Oxyz, cho mặt cầu (S) : (z − 2)2 + (y − 2)2 + (z − 2)2 = 12 và điểm A(4;4;0). Gọi B(a; b; c) là điểm thuộc mặt cầu (S) sao cho tam giác BOA cân tại B và diện tích tam giác OAB bằng Khi đó a + b + c bằng
Biết hàm số liên tục trên ℝ. Tính giá trị của biểu thức S = a + b.
Viện Công nghệ sinh học và Công nghệ thực phẩm của Trường Đại học Bách khoa Hà Nội đã hỗ trợ cho Công ty Thực phẩm lý tưởng theo cách nào sau đây?
Cho n là số nguyên dương thỏa mãn Số hạng không chứa x trong khai triển của biểu thức bằng
Cho phương trình Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thực?