Một bộ pha trà bằng thủy tinh có bình tổng và các tách đều là dạng hình trụ. Bình tổng có chiều cao gấp đôi đường kính đáy, tách trà có bán kính đáy bằng một nửa bán kính đáy bình tổng và có chiều cao bằng một phần ba chiều cao bình tổng. Có ba người ngồi thưởng trà, mỗi lượt người thưởng trà chỉ uống vừa đúng ba phần tư lượng nước có trong chén trà rồi lại châm thêm nước trà từ bình tổng vào chén. Hỏi sau mấy lần rót nước trà vào các chén thì hết nước trà trong bình tổng, biết rằng thể tích nước trà ban đầu có trong bình tổng chiếm ba phần tư thể tích của bình và mỗi lần rót trà thì chỉ rót vừa đủ ba phần tư thể tích của chén trà.

 Giải bởi Vietjack
Giải bởi Vietjack

Một vật chuyển động trong 4 giờ với vận tốc v(km/h) phụ thuộc thời gian t(h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2;9) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 4 giờ đó.
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1;0;1), B(1;0;−3) và điểm D có hoành độ âm. Mặt phẳng (ABCD) đi qua gốc tọa độ O. Khi đó đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có phương trình
Gọi S là tập hợp các số tự nhiên có 6 chữ số được lập từ tập A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 1400.
Có bao nhiêu giá trị nguyên dương của m để bất phương trình nghiệm đúng với mọi x ∈ (0;1)?
Cho hàm số , biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng
Từ thông tin tại đoạn cuối (dòng 43-53), nhận định nào sau đây là chính xác?
Cho hàm số y = f(x) có đạo hàm trên ℝ và có bảng biến thiên như sau:
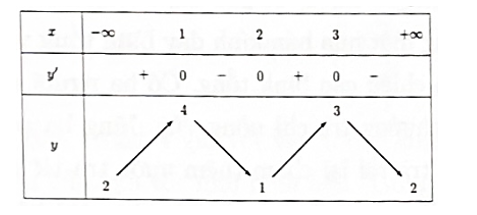
Tổng các giá trị nguyên của tham số m để phương trình có đúng hai nghiệm phân biệt bằng
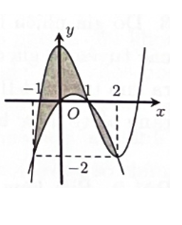
Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
Trong hệ trục tọa độ Oxyz, cho mặt cầu (S) : (z − 2)2 + (y − 2)2 + (z − 2)2 = 12 và điểm A(4;4;0). Gọi B(a; b; c) là điểm thuộc mặt cầu (S) sao cho tam giác BOA cân tại B và diện tích tam giác OAB bằng Khi đó a + b + c bằng
Biết hàm số liên tục trên ℝ. Tính giá trị của biểu thức S = a + b.
Viện Công nghệ sinh học và Công nghệ thực phẩm của Trường Đại học Bách khoa Hà Nội đã hỗ trợ cho Công ty Thực phẩm lý tưởng theo cách nào sau đây?
Cho n là số nguyên dương thỏa mãn Số hạng không chứa x trong khai triển của biểu thức bằng
Cho phương trình Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thực?