Hình thang ABCD (AB//CD) có AB = 4cm; MN = 6cm với M và N lần lượt là trung điểm của BC và AD. Khi đó độ dài cạnh CD là?
 Giải bởi Vietjack
Giải bởi Vietjack
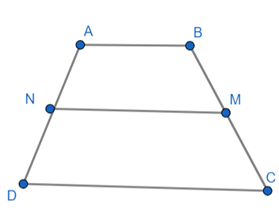
M, N lần lượt là trung điểm của BC và AD nên MN là đường trung bình của hình thang ABCD
⇒ MN = (AB + CD) : 2
⇒ CD = 2MN - AB = 2.6 - 4 = 8 (cm).
Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD.
Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O).
a) Chứng minh AB2 = AD.AE.
b) Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp, chứng minh HB là tia phân giác của
Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin
Một số học sinh dự thi học sinh giỏi toán. Nếu xếp 25 học sinh vào một phòng thì còn thừa 5 học sinh chưa có chỗ. Nếu xếp 28 học sinh vào một phòng thì thừa 1 phòng. Tìm số học sinh dự thi?
Một lớp học có 28 nam và 24 nữ. Có bao nhiêu cách chia đều số học sinh vào các tổ với số tổ nhiều hơn sao cho số nam trong các tổ bằng nhau và số nữ trong các tổ bằng nhau? Cách chia nào để mỗi tổ có ít học sinh nhất?
Hai số lẻ có tổng là số nhỏ nhất có 4 chữ số và ở giữa hai số lẻ đó có 4 số lẻ tìm hai số đó.
Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.
Một mảnh vườn hình chữ nhật có chu vi bằng chu vi của một thửa ruộng hình vuông cạnh 80m. Nếu giảm chiều dài mảnh vườn đi 30m và tăng chiều rộng thêm 10m thì mảnh vườn sẽ có hình vuông. Tính diện tích mảnh vườn?
Một cột đèn có bóng trên mặt đất dài 8,5m . Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 38°. Tính chiều cao của cột đèn ? (Kết quả làm tròn đến 1 chữ số thập phân).