Cho ∆ ABC nhọn, đường cao AH. Kẻ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC).
a) Chứng minh: ∆AEH ∽ ∆AHB. Từ đó suy ra AH2 = AE.AB.
b) Chứng minh AE. AB = AF.AC.
c) Cho chu vi các ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm. Tính diện tích ∆AEF và ∆ACB biết diện tích ∆ACB lớn hơn diện tích ∆AEF là 25 cm2.
Giải bởi Vietjack
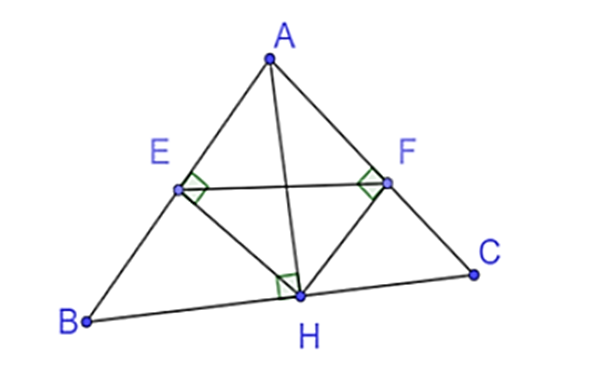
a) Vì AH là đường cao (giả thiết)
AH ⊥ BC
∆AHB vuông tại H
Lại có HE ⊥ AB (giả thiết)
∆AEH vuông tại E
Do đó
Xét ∆AEH và ∆AHB có:
(chứng minh trên)
chung
Do đó ∆AEH ∽ ∆ AHB (g.g)
⇒ (tỉ số đồng dạng)
Suy ra: AH2 = AE.AB. (1)
b) Vì AH ⊥ BC (chứng minh câu a) nên
Vì HF ⊥ AC (giả thiết) nên
Xét ∆AFH và ∆AHC có
chung
Do đó ∆AFH ᔕ ∆AHC (g.g)
⇒ (tỉ số đồng dạng)
Suy ra: AH2 = AF.AC. (2)
Từ (1) và (2) suy ra: AE. AB = AF.AC
c) Theo b có: AE. AB = AF.AC nên:
Xét ∆AEF và ∆ACB có
chung
Do đó ∆AEF ᔕ ∆ACB (c.g.c)
⇒
Theo tính chất dãy tỉ số bằng nhau ta có:
(vì chu vi ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm)
(Do SABC – SAEF = 25 cm2)
Vậy SAEF = 5.4 = 20 (cm2)
SABC = 20 + 25 = 45 (cm2).
Từ 1 điểm A ở bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Chứng minh OA là trung trực của đoạn BC.
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Tính số đo góc
Cho góc . Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) DEAB = DECD.
c) OE là tia phân giác của góc xOy.
Cho tam giác nhọn ABC. Vẽ ra phía ngoài của tam giác này các tam giác ABD và tam giác ACE vuông cân tại A. Gọi M là trung điểm của DE. Chứng minh rằng hai đường thẳng MA và BC vuông góc với nhau.
Một ô tô chạy 100km hết 12 lít xăng. Hỏi cần bao nhiêu lít xăng khi ô tô chạy quãng đường thứ nhất 138km và quãng đường thứ hai 162km?
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3 + 2x2 + (m − 3)x + m
có hai điểm cực trị và điểm M(9; −5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị.
Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC. Chứng minh BC.BE.CF = AH3.
cho hình bình hành ABCD, đường chéo AC lớn hơn đường chéo BD, kẻ CH vuông góc với AD, CK vuông góc với AB.
a, Chứng minh tam giác BCK đồng dạng tam giác DCH.
b, Chứng minh tam giác CKH đồng dạng tam giác BCA.
c, Chứng minh HK = AC.sin
d, Tính diện tích của tứ giác AKCH nếu , AB = 4cm, AC = 5cm.
Một cung lượng giác trên đường tròn định hướng có độ dài bằng một nửa bán kính. Số đo theo rađian của cung đó là?
Trên mặt phẳng tọa độ Oxy cho đường thẳng d: y = (2m + 10)x - 4m - 1 và điểm A(-2;3). Tìm m để khoảng cách từ A đến đường thẳng lớn nhất.
Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Qua A kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Vẽ tia Ax nằm giữa tia AB và tia AO cắt đường tròn (O) tại hai điểm C và D (C nằm giữa A và D). Gọi M là trung điểm của dây CD, kẻ BH vuông góc với AO tại H.
a, Tính tích OH.OA theo R.
b, Chứng minh 4 điểm A, B, M, O cùng thuộc một đường tròn.
c, Gọi E là giao điểm của OM với HB. Chứng minh ED là tiếp tuyến của đường tròn (O;R).
Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ
