Cho hình chóp S.ABC, các tam giác ABC và SBC là các tam giác nhọn. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC. Khẳng định nào sau đây là đúng?
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
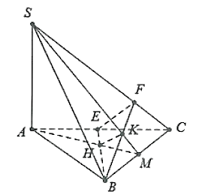
Giả sử AH vuông góc với BC tại M
Ta có:
BC vuông góc với AM
BC vuông góc với SA
Do đó, BC ⊥ (SAM).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên SAB là tam giác đều, SCD là tam giác vuông cân đỉnh S. Gọi I, J lần lượt là trung điểm của AB và CD. Gọi H là hình chiếu của S lên IJ, đường thẳng SH vuông góc với mặt phẳng nào sau đây?
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, điểm I và H lần lượt là trung điểm của AB và BC. Trên đoạn CI và SA lần lượt lấy hai điểm M, N sao cho MC = 2MI, NA = 2NS. Biết SH ⊥ (ABC). Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và tam giác ABC vuông ở B, AH là đường cao của ∆SAB. Khẳng định nào sau đây sai?
Cho hình chóp S.ABC, các tam giác ABC và SBC là các tam giác nhọn. Gọi H và K lần lượt là trực tâm của tam giác ABC và SBC. Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi O và có SA = SC, SB = SD. Khẳng định nào sau đây là đúng?
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABC có cạnh SA ⊥(ABC) và đáy ABC là tam giác cân ở C. Gọi H và K lần lượt là trung điểm của AB và SB. Khẳng định nào sau đây là sai?