Cho hình chóp S.MNPQ, MNPQ là vuông, A là trung điểm của MN, B là trung điểm của QP, C là trung điểm của MQ, D là trung điểm của NP. Đường thẳng SC vuông góc với đường thẳng nào dưới đây?
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
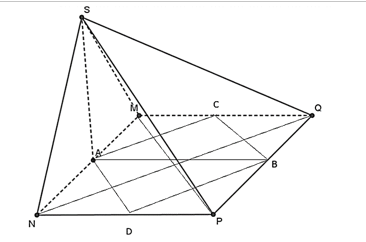
Vì SA vuông góc với đáy nên hình chiếu vuông góc của S lên (MNPQ) là A.
Vì C thuộc (MNPQ) nên hình chiếu vuông góc của C lên (MNPQ) là C.
Do đó, hình chiếu vuông góc của SC lên (MNPQ) là AC.
Vì MNPQ là hình vuông nên:
MP ⊥ NQ, MP = NQ
Vì A, B, C, D lần lượt là trung điểm của của MN, PQ, MQ, NP
Do đó, ACBD là hình vuông.
Suy ra: AC ⊥ CB
Vậy SC ⊥ CB (theo định lí ba đường vuông góc).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, H là tâm hình vuông ABCD, SH ⊥ (ABCD). Đường thẳng SA vuông góc với đường thẳng nào sau đây?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Kẻ AH ⊥ SB tại H, AK ⊥ SB tại K. Khẳng định nào sau đây là sai?
Hình chóp tam giác đều S.ABC có cạnh bên bằng cạnh đáy, K là trung điểm của AB. Khẳng định nào sau đây sai?
Cho hình chóp S.MNPQ, MNPQ là hình chữ nhật, trung điểm A của MN là hình chiếu vuông góc của S lên đáy, B là trung điểm của QP. Đường thẳng SN vuông góc với đường thẳng nào dưới đây?
Hình chóp tam giác đều S.ABC có cạnh bên bằng cạnh đáy. Đường thẳng SA vuông góc với đường thẳng nào sau đây?
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = a. SA vuông góc với đáy. Gọi M là trung điểm của AD. Đường thẳng BM vuông góc với đường thẳng:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Đường thẳng SB vuông góc với đường thẳng nào sau đây?