Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d1 và d2 cùng đi qua O và vuông góc với nhau. Đường thẳng d1 cắt các cạnh AB và CD ở M và P. Đường thẳng d2 cắt các cạnh BC và AD ở N và Q.
a/ Chứng minh tứ giác MNPQ là hình thoi.
b/ Nếu ABCD là hình vuông thì tứ giác MNPQ là hình gì? Hãy chứng minh.
Giải bởi Vietjack
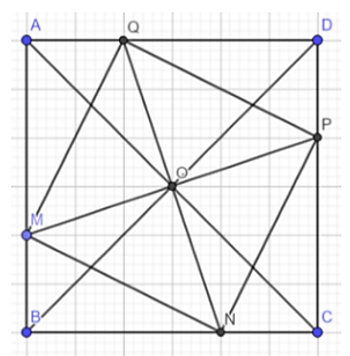
a/ Ta có ABCD là hình bình hành nên AC cắt BD tại trung điểm O mỗi đường
Nên OA = OC; OB = OD
Mà AB // CD nên
Nên OM = OP hay O là trung điểm MP
Tương tự: O là trung điểm NQ
Vì d1 vuông góc d2 tức NQ vuông góc MP
Suy ra: NQ ⊥ MP = O là trung điểm mỗi đường
Vậy MNPQ là hình thoi
b/ Nếu ABCD là hình vuông thì AC ⊥ BD
Suy ra:
Mà OB = OC;
Xét tam giác OBM và tam giác OCN có:
OB = OC
Nên: ∆OBM = ∆OCN (g.c.g)
Suy ra: OM = ON
Kết hợp phần a nên MNPQ là hình vuông.
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0.
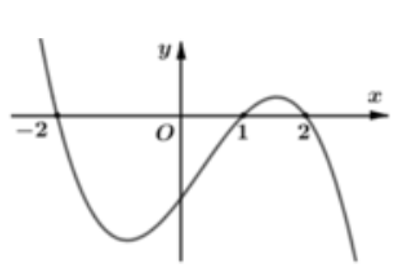
Hàm số g( x) = [f(3 - x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1).
B. (1; 2).
C. (2; 5).
D. ( 5 ; +∞).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
