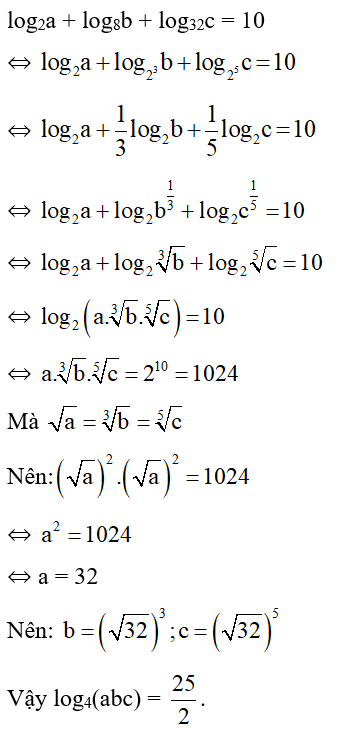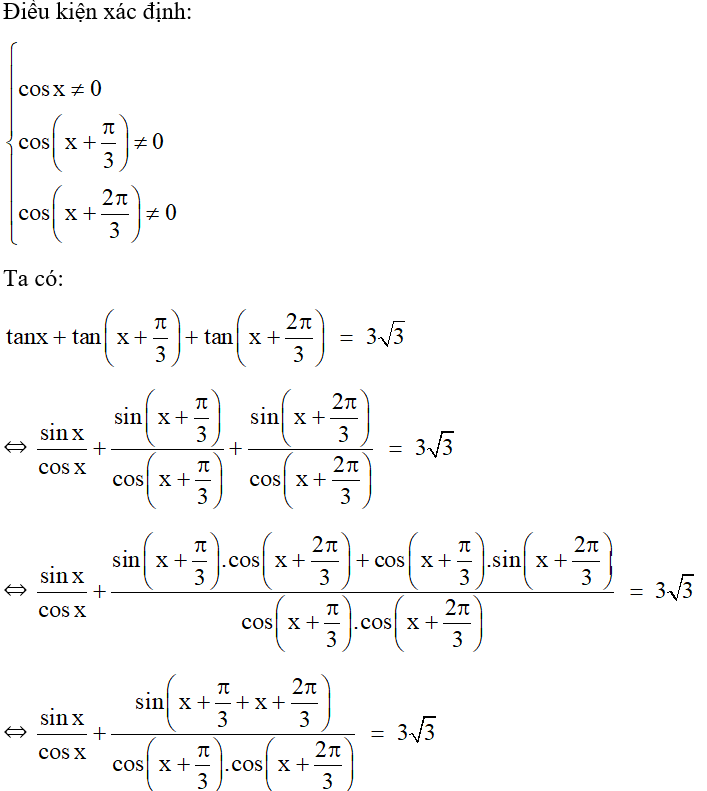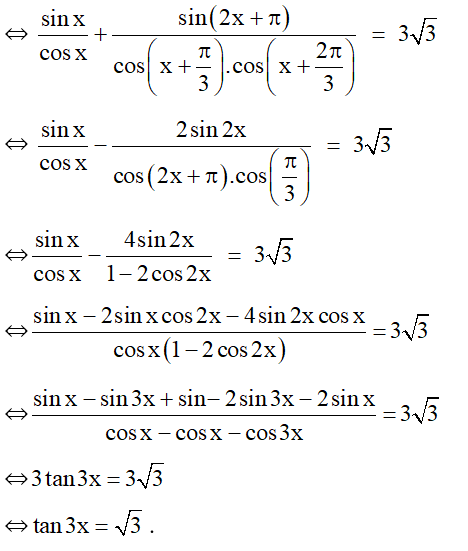87 câu hỏi trắc nghiệm thuộc Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 90) - vietjack.online

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án

Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 90)

11012 lượt thi
87 câu hỏi
60 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d₁ và d₂ cùng đi qua O và vuông góc với nhau. Đường thẳng d₁ cắt các cạnh AB và CD ở M và P. Đường thẳng d₂ cắt các cạnh BC và AD ở N và Q.

a/ Chứng minh tứ giác MNPQ là hình thoi.

b/ Nếu ABCD là hình vuông thì tứ giác MNPQ là hình gì? Hãy chứng minh.

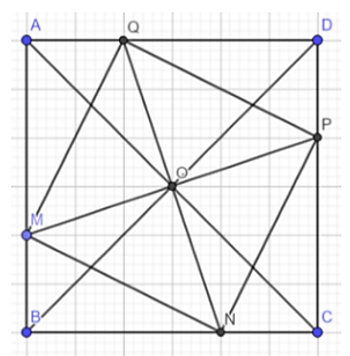
Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d1 và d2 (ảnh 1)

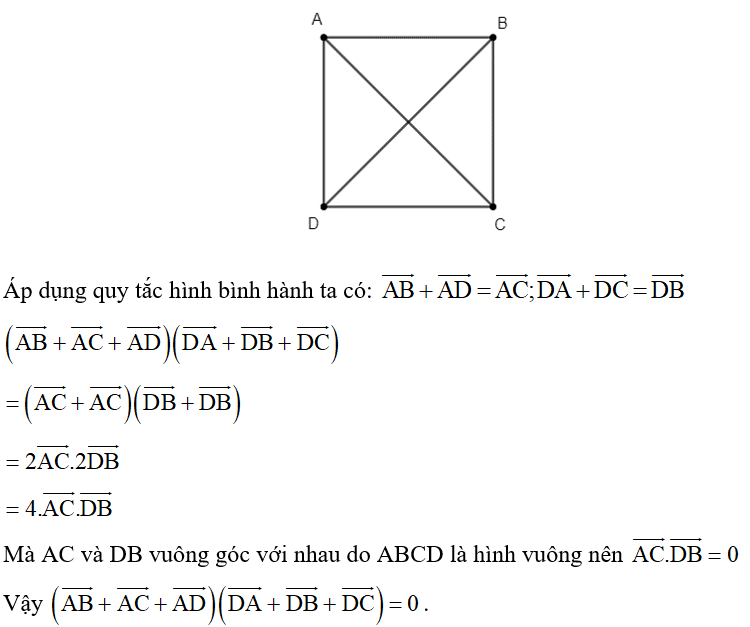
a/ Ta có ABCD là hình bình hành nên AC cắt BD tại trung điểm O mỗi đường

Nên OA = OC; OB = OD

Mà AB // CD nên $\frac{O M}{O P} = \frac{O A}{O C} = 1$

Nên OM = OP hay O là trung điểm MP

Tương tự: O là trung điểm NQ

Vì d₁ vuông góc d₂ tức NQ vuông góc MP

Suy ra: NQ ⊥ MP = O là trung điểm mỗi đường

Vậy MNPQ là hình thoi

b/ Nếu ABCD là hình vuông thì AC ⊥ BD

Suy ra: $\hat{M O B} = 90 ° - \hat{B O N} = \hat{N O C}$

Mà OB = OC; $\hat{O B M} = \hat{O B A} = 45 ° = \hat{O C B} = \hat{O C N}$

Xét tam giác OBM và tam giác OCN có:

$\hat{O B M} = \hat{O C N}$

OB = OC

$\hat{M O B} = \hat{N O C}$

Nên: ∆OBM = ∆OCN (g.c.g)

Suy ra: OM = ON

Kết hợp phần a nên MNPQ là hình vuông.

Câu 2:

Cho hình thang ABCD (AB // CD) có AB = 1cm, CD = 5cm và $\hat{C}$ = 30°, $\hat{D}$ = 60°. Tính diện tích hình thang ABCD.

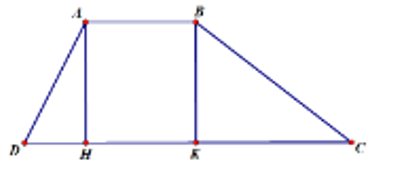
Cho hình thang ABCD (AB // CD) có AB = 1cm, CD = 5cm (ảnh 1)

Kẻ đường cao AH và đường cao BK ⇒ AB = HK = 1cm

Nên ta có: DH + CK = 4 (1)

Theo tỉ số lượng giác cho tam giác ADH và BCK ta lại có:

AH = tan60°. DH

BK = tan 30°. CK

Nên: tan60°. DH = tan30°. CK (2)

Từ (1) và (2) giải ra ta được: DH = 1cm, CK = 3cm.

Suy ra: AH = tan60°. DH = $\sqrt{3} (c m)$

S_ABCD = $\frac{1}{2} . A H . (A B + C D) = \frac{1}{2} . \sqrt{3} . (1 + 5) = 3 \sqrt{3} (c m^{2})$ .

Câu 3:

Cho hình thang cân ABCD có đáy lớn AB = 30 cm, đáy nhỏ CD = 10 cm và

\hat{A}

= 60°. Tính cạnh BC.

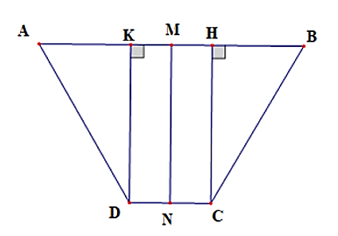
Cho hình thang cân ABCD có đáy lớn AB = 30 cm, đáy nhỏ CD = 10 cm (ảnh 1)

Kẻ CH ⊥ AB, DK ⊥ AB

Suy ra DK // CH (quan hệ từ vuông góc đến song song)

Mà CD // HK

Suy ra CDKH là hình bình hành

Lại có $\hat{C H K}$ = 90° nên CDKH là hình chữ nhật

Suy ra KH = CD = 10 (cm)

Vì ABCD là hình thang cân nên AD = BC và $\hat{A} = \hat{B} = 60 °$

Xét ∆AKD và ∆BHC có

$\hat{A} = \hat{B} = 60 °$ (chứng minh trên);

AD = BC (chứng minh trên);

$\hat{A K D} = \hat{B H C} = 90 °$

Do đó ∆AKD = ∆BHC (cạnh huyền – góc nhọn)

Suy ra AK = BH

Ta có AB = AK + KH + BH = 30

Hay 2AK + 10 = 30

Suy ra AK = BH = 10 (cm)

Xét tam giác BCH vuông ở H

Suy ra: $B C = \frac{B H}{\cos \hat{B}} = \frac{10}{\cos 60 °} = 20 (c m)$ .

Câu 4:

Cho hình thoi ABCD có cạnh AB = 8cm. Tính chu vi hình thoi ABCD?

Cho hình thoi ABCD có cạnh AB = 8cm. Tính chu vi hình thoi ABCD? (ảnh 1)

Vì hình thoi có 4 cạnh bằng nhau nên mỗi cạnh đều bằng 8cm.

Chu vi hình thoi là: 8.4 = 32 (cm).

Câu 5:

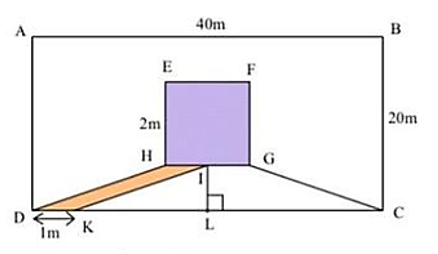
Mảnh vườn hình chữ nhật ABCD có kích thước như hình vẽ. Ở chính giữa mảnh vườn người ta xây 1 cái chòi hình vuông EFGH có cạnh EH = 2m; một lối đi ra chòi hình bình hành DHIK có cạnh DK = 1m.

a) Tính diện tích mảnh vườn hình chữ nhật ABCD.

b) Người ta trồng rau trên mảnh đất hình thang IGCK và trồng hoa trên phần đất còn lại. Tính diện tích lối đi, diện tích trồng rau và diện tích trồng hoa.

Mảnh vườn hình chữ nhật ABCD có kích thước như hình vẽ. Ở chính giữa mảnh (ảnh 1)

a) Diện tích mảnh vườn hình chữ nhật ABCD là:

S_ABCD = AB.BC = 40.20 = 800 (m²)

b) Chòi hình vuông nằm chính giữa mảnh vườn

⇒ IL = (20 − 2) : 2 = 9m

Lối đi hình bình hành DHIK có đường cao là IL = 9m ứng với cạnh đáy DK = 1m

Diện tích lối đi hình bình hành DHIK là: S_DHIK = IL.DK = 9.1 = 9 (m²)

IG = HG – HI = 2 – 1 = 1m

CK = CD – DK = 40 – 1 = 39m

Diện tích trồng rau hình thang IGCK là:

S_IGCK = $\frac{1}{2}$ IL.(IG + CK) = 180 (m2)

Diện tích chòi hình vuông EFGH là:

S_EFGH= EH.EH = 2.2 = 4 (m²)

Diện tích trồng hoa là:

S_ABCD− S_DHIK− S_IGCK− S_EFGH= 800 – 9 – 180 – 4 = 607 (m²).

Câu 6:

Cho chóp S.ABCD có đáy hình bình hành tâm O. Lấy N, M lần lượt thuộc SA, SB sao cho $B M = \frac{1}{4} B S, S N = \frac{3}{4} S A$ . Tìm giao tuyến của:

a) (OMN) và (SAB).

b) (OMN) và (SAD).

c) (OMN) và (SBC).

d) (OMN) và (SCD).

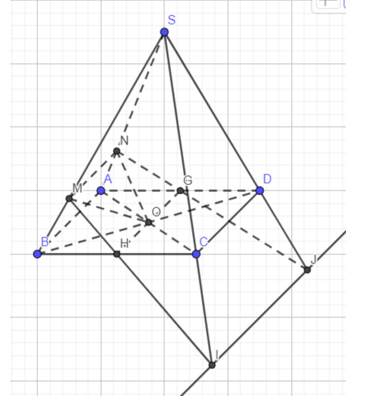
Cho chóp S.ABCD có đáy hình bình hành tâm O. Lấy N, M lần lượt thuộc SA, SB sao cho (ảnh 1)

a) $\{\begin{cases} M \in (O M N), M \in (S A B) \\ N \in (O M N), N \in (S A B) \end{cases}$

Nên: (OMN) ∩ (SAB) = MN

b) Ta có: $\frac{S M}{S B} = \frac{S N}{S A} = \frac{3}{4}$ nên MN // AB

Kẻ đường thẳng qua O và song song với AB cắt AD, BC lần lượt tại G, H

⇒ G, H ∈ (OMN)

Khi đó: (OMN) ∩ (SAD) = GN

c) $\{\begin{cases} M \in (O M N), M \in (S B C) \\ H \in (O M N), H \in (S B C) \end{cases}$

Nên (OMN) ∩ (SBC) = MH

d) Gọi giao điểm của MH và SC là I; giao điểm của NG và SD là J

Ta có: $\{\begin{cases} I \in (O M N), I \in (S C D) \\ J \in (O M N), J \in (S C D) \end{cases}$

Nên (OMN) ∩ (SCD) = IJ.

Câu 7:

Cho tam giác ABC vuông tại A đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng $\frac{S_{A M N}}{S_{A B C}} = \sin^{2} B . \sin^{2} C$ .

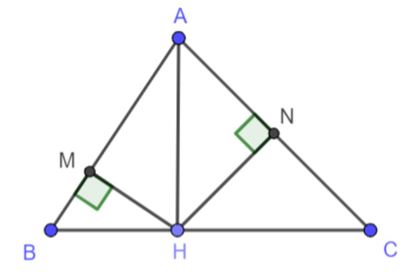
Cho tam giác ABC vuông tại A đường cao AH. Gọi M, N lần lượt là hình chiếu của H (ảnh 1)

Ta có: HM ⊥ AB, HN ⊥ AC, AB ⊥ AC

Nên AMHN là hình chữ nhật

⇒ AH = MN

⇒ $\hat{A M N} = \hat{M A H} = \hat{B A H} = 90 ° - \hat{B} = \hat{A C B}$

Mà $\hat{M A N} = \hat{B A C}$

⇒ ∆ANM ∽ ∆ABC (g.g)

⇒ $\frac{S_{A M N}}{S_{A B C}} = {(\frac{M N}{B C})}^{2} = \frac{A H^{2}}{B C^{2}}$
Ta có: 1 – cos²B = sin²B

⇒ (1 – cos²B)sin²C = sin²Bsin²C = (sinBsinC)²

= ${(\frac{A C}{B C} . \frac{A B}{B C})}^{2} = {(\frac{A B . A C}{B C^{2}})}^{2} = {(\frac{A H . B C}{B C^{2}})}^{2} = {(\frac{A H}{B C})}^{2}$

⇒ $\frac{S_{A M N}}{S_{A B C}} = (1 - c o s^{2} B) s i n^{2} C$

⇒ $\frac{S_{A M N}}{S_{A B C}} = \sin^{2} B . \sin^{2} C$

Câu 8:

Trên mặt phẳng tọa độ cho các điểm A, B, C có tọa độ A(0; 4), B(3; 4), C(3; 0). Hãy tìm hệ số a sao cho đường thẳng y = ax chia hình chữ nhật OABC thành hai phần, trong đó diện tích phần chứa điểm A gấp đôi diện tích phần C.

Diện tích hình chữ nhật OABC là: 3.4 = 12(đvdt)

Do diện tích phần chứa điểm A gấp đôi diện phần phần chứa điểm C do đó đường thẳng y = ax sẽ cắt đoạn BC tại một điểm, gọi điểm đó là điểm D.

Diện tích tam giác ODC là: 12 : (2 + 1) . 1 = 4 (đvdt)

Độ dài đoạn DC: $4.2 : 3 = \frac{8}{3}$

Nên tọa độ điểm $D (3; \frac{8}{3})$ .

Câu 9:

Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM có chu vi bằng 180 cm và chiều dài MN gấp 4 lần chiều rộng CN.

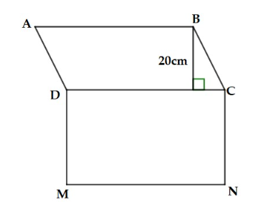
Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM (ảnh 1)

Nửa chu vi hình chữ nhật DCNM là: 180 : 2 = 90 (cm)

Khi đó: MN + CN = 90 (cm)

Chiều dài MN gấp 4 lần chiều rộng CN

Tổng số phần bằng nhau là:

1 + 4 = 5 (phần)

Chiều dài MN (hay CD) của hình chữ nhật DCNM là:

90 : 5 . 4 = 72 (cm)

Chiều rộng CN (hay DM) của hình chữ nhật DCNM là:

90 – 72 = 18 (cm)

Diện tích hình chữ nhật DCMN là:

18 . 72 = 1296 (cm²)

Diện tích hình bình hành ABCD là:

72 . 20 = 1440 (cm²)

Diện tích hình H là:

1296 + 1440 = 2736 (cm²).

Câu 10:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 11:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 12:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 13:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 14:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 15:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 16:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 17:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 18:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 19:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 20:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 21:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 22:

Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và (ảnh 1)

Câu 23:

Tìm x biết (x + 1)⁵ = 243.

(x + 1)⁵ = 243

⇔ (x + 1)⁵ = 3⁵

⇔ x + 1 = 3

⇔ x = 2

Vậy x = 2.

Câu 24:

Tìm x biết ${(x - \frac{1}{2})}^{2} - \frac{1}{3} = \frac{22}{12}$ .

${(x - \frac{1}{2})}^{2} - \frac{1}{3} = \frac{22}{12}$

⇔ ${(x - \frac{1}{2})}^{2} = \frac{13}{6}$

⇔ $[\begin{array}{l} x - \frac{1}{2} = \sqrt{\frac{13}{6}} \\ x - \frac{1}{2} = - \sqrt{\frac{13}{6}} \end{array}$

⇔ $[\begin{array}{l} x = \sqrt{\frac{13}{6}} + \frac{1}{2} \\ x = - \sqrt{\frac{13}{6}} + \frac{1}{2} \end{array}$ .

Câu 25:

Tìm x biết (x – 3)³ – (x – 3)(x² + 3x + 9) + 9(x + 1)² = 15.

(x – 3)³ – (x – 3)(x² + 3x + 9) + 9(x + 1)² = 15

x³ – 9x² + 27x – 27 – (x³ + 3x² + 9x – 3x² – 9x – 27) + 9(x² + 2x + 1) – 15 = 0

x³ – 9x² + 27x – 27 – x³ + 27 + 9x² + 18x + 9 – 15 = 0

45x – 6 = 0

x = $\frac{6}{45}$ .

Câu 26:

Phân tích thành nhân tử: 12x² – 72x + 60.

12x² – 72x + 60

= 12x² – 12x – 60x + 60

= 12x(x – 1) – 60(x – 1)

= (x – 1)(12x – 60)

= 12(x – 1)(x – 5).

Câu 27:

2 ngày 16 giờ = … ngày.

2 ngày 16 giờ = $2 \frac{16}{24} = 2 \frac{2}{3} = \frac{8}{3}$ ngày.

Câu 28:

Tính giá trị biểu thức: $\frac{1}{\sqrt{5} - 2} + \frac{1}{\sqrt{5} + 2}$ .

$\frac{1}{\sqrt{5} - 2} + \frac{1}{\sqrt{5} + 2} = \frac{\sqrt{5} + 2 + \sqrt{5} - 2}{(\sqrt{5} - 2) (\sqrt{5} + 2)} = \frac{2 \sqrt{5}}{5 - 4} = 2 \sqrt{5}$

Câu 29:

Lấy số 196 chia cho số nguyên a rồi cộng thêm a. Sau đó, lấy kết quả này chia cho a rồi cộng thêm a. Kết quả thu được là 26a. Hãy tìm a.

Ta có: 196 : a + a = X (1)

X : a + a = 26a

⇔ X : a = 25a

⇔ X = 25a.a = 25a² (2)

Thay (2) vào (1) có:

196 : a + a = 25a²

⇔ $\frac{196}{a} = 25 a^{2} - a$

⇔ 25a³ – 196 – a² = 0

⇔ (a – 2)(25a² + 49a + 98) = 0

⇔ a = 2 (vì phương trình 25a² + 49a + 98 = 0 vô nghiệm)

Vậy a = 2.

Câu 30:

Tìm tất cả các giá trị thực của tham số m để hàm số y = x³ – 3mx² – 9m²x nghịch biến trên khoảng (0; 1).

Ta có: y = x³ – 3mx² – 9m²x

y’ = 3x² – 6mx – 9m²

y’ = 3(x² – 2mx – 3m²)

y’ = 3(x + m)(x – 3m)

TH1: m > 0 suy ra y’ < 0 ⇔ –m < x < 3m

Nên hàm số nghịch biến trên (0; 1)

Suy ra: $\{\begin{cases} 3 m > 1 \\ - m < 0 \end{cases} \Leftrightarrow m > \frac{1}{3}$

TH2: m < 0 suy ra y’ < 0 ⇔ 3m < x < –m

Nên hàm số nghịch biến trên (0; 1)

Suy ra: $\{\begin{cases} 3 m < 0 \\ - m > 1 \end{cases} \Leftrightarrow m < - 1$

TH3: m = 0 suy ra y’ = 3x² ≥ 0; ∀ x ∈ (0; 1) nên hàm số đồng biến trên ℝ.

Vậy $m > \frac{1}{3}$ hoặc m < – 1.

Câu 31:

Tìm các giá trị của m để phương trình x² – 2(m – 1)x + 2m – 3 = 0 có 2 nghiệm phân biệt x₁, x₂ thỏa mãn $|x_{1} - x_{2}| = 5$ với m là tham số.

Xét phương trình: x² – 2(m – 1)x + 2m – 3 = 0

Ta có: ∆’ = m² – 4m + 4 = (m – 2)² > 0 với mọi m khác 2.

Vậy phương trình đã cho luôn có 2 nghiệm phân biệt khi m ≠ 2.

Áp dụng Vi-ét: $\{\begin{cases} x_{1} + x_{2} = 2 (m - 1) \\ x_{1} x_{2} = 2 m - 3 \end{cases}$

Theo bài ra: $|x_{1} - x_{2}| = 5$

⇒ ${(x_{1} - x_{2})}^{2} = 25$

⇔ ${(x_{1} + x_{2})}^{2} - 4 x_{1} x_{2} = 25$

⇔ 4(m – 1)² – 4(2m – 3) – 25 = 0

⇔ 4m² – 16m – 9 = 0

⇔ (2m – 9)(2m + 1) = 0

⇔ $[\begin{array}{l} m = \frac{9}{2} \\ m = - \frac{1}{2} \end{array}$ .

Câu 32:

Xác định tính đúng sai của các mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “∃n ∈ ℕ, n chia hết cho n + 1”.

Với n = 0, n + 1 = 1, khi đó 0 chia hết cho 1.

Suy ra mệnh đề Q là mệnh đề đúng.

Mệnh đề phủ định của mệnh đề Q là: $\bar{Q}$ : “∀n ∈ ℕ, n không chia hết cho n + 1”.

Đây là mệnh đề sai.

Câu 33:

Tìm 3 giá trị của x biết $0,2 < x < \frac{3}{10}$ .

$0,2 < x < \frac{3}{10}$

Hay $0,2 < x < 0,3$

Nên 3 giá trị của x có thể là 0,21; 0,22; 0,23.

Câu 34:

Tính giá trị biểu thức A = $1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!}$ .

Tính giá trị biểu thức A = 1+ 1/1! +1/ 2! +1/ 3! +1/4!. (ảnh 1)

Câu 35:

Chứng minh $\frac{1}{2^{2}} + \frac{1}{3^{2}} + ... + \frac{1}{100^{2}} < 1$ .

Chứng minh 1/ 2^2 +1/ 3^2 +..+ 1/ 100^2 nhỏ hơn 1 . (ảnh 1)

Câu 36:

Tính A = 1 + 2 + 2² + 2³ + … + 2²⁰²¹.

A = 1 + 2 + 2² + 2³ + … + 2²⁰²¹

2A = 2 + 2² + 2³ + … + 2²⁰²²

Ta có: 2A – A = (2 + 2² + 2³ + … + 2²⁰²²) – (1 + 2 + 2² + 2³ + … + 2²⁰²¹)

A = 2²⁰²² – 1.

Câu 37:

Chứng minh rằng: 10⁹ + 10⁸ + 10⁷ chia hết cho 222 và chia hết cho 555.

Ta có: 10⁹ + 10⁸ + 10⁷

= 10⁷(10² + 10 + 1)

= 10⁷.111

= 2⁷.5⁷.111

= 2⁶.5⁷.222 ⋮ 222

Vậy 10⁹ + 10⁸ + 10⁷ chia hết cho 222.

Lại có: 10⁹ + 10⁸ + 10⁷

= 10⁷(10² + 10 + 1)

= (2.5)⁷(10² + 10 + 1)

= 2⁷.5⁶.5.111

= 2⁷.5⁶.555 ⋮ 555

Vậy 10⁹ + 10⁸ + 10⁷ chia hết cho 555.

Câu 38:

Chứng minh rằng: 13ⁿ − 1 chia hết cho 12.

Ta có: 13ⁿ − 1

= (13 – 1)(13^n-1 + 13^n-2 + … + 13¹ + 1)

= 12.(13^n-1 + 13^n-2 + … + 13¹ + 1) ⋮ 12

Vậy 13ⁿ − 1 chia hết cho 12.

Câu 39:

Tìm 2 số hữu tỉ a và b, sao cho a + b = ab = a : b.

a + b = ab

⇒ a = ab - b = b(a - 1)

Thay a = b - 1 vào a + b = a : b ta có:

a + b = a -1

⇔ a + b - a = -1

⇔ b = -1

Ta có:

ab = a + b

⇔ - 1 .a = a + - 1

⇔ - a = a - 1

⇔ -a - a = -1

⇔ -2a = -1

⇔ $a = \frac{1}{2}$

Vậy $a = \frac{1}{2}; b = - 1$ .

Câu 40:

Chứng minh 19¹⁹ + 69¹⁹ chia hết cho 44.

19¹⁹ + 69¹⁹ = (19 + 69)(19¹⁸ - 19¹⁷.69 + … + 69¹⁸)

= 88.(19¹⁸ - 19¹⁷.69 + … + 69¹⁸)

= 2.44.(19¹⁸ - 19¹⁷.69 + … + 69¹⁸)

Mà 44 ⋮ 44 nên 2.44.(19¹⁸ - 19¹⁷.69 + … + 69¹⁸) ⋮ 44

Vậy 19¹⁹ + 69¹⁹ chia hết cho 44.

Câu 41:

Chứng minh 2²⁰²⁰ + 2²⁰²¹ + 2²⁰²² + 7²⁰²³ + 7²⁰²⁴ chia hết cho 7.

2²⁰²⁰ + 2²⁰²¹ + 2²⁰²² + 7²⁰²³ + 7²⁰²⁴

= 2²⁰²⁰(1 + 2 + 2²) + 7.(7²⁰²² + 7²⁰²³)

= 2²⁰²⁰.7 + 7.(7²⁰²² + 7²⁰²³)

= 7(2²⁰²⁰ + 7²⁰²² + 7²⁰²³) ⋮ 7

Vậy 2²⁰²⁰ + 2²⁰²¹ + 2²⁰²² + 7²⁰²³ + 7²⁰²⁴ chia hết cho 7.

Câu 42:

Tìm số tự nhiên n để 2n + 3 chia hết cho 3n + 1.

Ta có : 2n + 3 chia hết cho 3n + 1

⇒ 6n + 9 chia hết cho 3n + 1

⇒ 6n + 2 + 7 chia hết cho 3n + 1

⇒ 7 chia hết cho 3n + 1

⇒ 3n + 1 thuộc Ư(7) = {1;7}

Suy ra: n = 0; 2.

Câu 43:

Tìm số tự nhiên n để 3n + 4 chia hết cho n – 1.

Vì 3n + 4 = 3n + 7 – 3 = 3n – 3 + 7 = 3(n – 1) + 7

Do 3(n – 1) chia hết cho n – 1 (tính chất chia hết của một tích)

Nên để 3n + 4 chia hết cho n – 1 thì 7 phải chia hết cho n – 1 (tính chất chia hết của một tổng)

Hay (n – 1) thuộc Ư(7) = {1; 7}

Với n – 1 = 1 thì n = 2

Với n – 1 = 7 thì n = 8

Vậy với n = 2 hoặc n = 8 thì 3n + 4 chia hết cho n – 1.

Câu 44:

Tìm tất cả các số tự nhiên x biết 3x - 12 chia hết cho x – 2.

Ta có:

3x – 12 = 3x – 6 – 6 = 3(x − 2) − 6

Mà [3(x − 2)] ⋮ (x − 2) nên 6 ⋮ (x − 2)

⇒ (x − 2) ∈ Ư(6)

Vì x ∈ ℕ nên x ≥ 0

⇒ x – 2 ≥ −2

⇒ (x − 2) ∈ {−2; −1; 1; 2; 3; 6}

⇒ x ∈ {0; 1; 3; 4; 5; 8}

Vậy để (3x − 12) ⋮ (x − 2) thì x ∈ {0; 1; 3; 4; 5; 8}.

Câu 45:

Cho A = 2 . 4 . 6 . 8 . 10 . 12 + 40. Hỏi A có chia hết cho 80 không? Vì sao?

Để chứng minh A chia hết cho 80 ta chứng minh A chia hết cho 8 và 10.

Ta thấy: 2 . 4 . 6 . 8 . 10 . 12 ⋮ 10 và 40 ⋮ 10

Nên: 2 . 4 . 6 . 8 . 10 . 12 + 40 ⋮ 10 hay A ⋮ 10

Lại có: 2 . 4 . 6 . 8 . 10 . 12 ⋮ 8 và 40 ⋮ 8

Nên: 2 . 4 . 6 . 8 . 10 . 12 + 40 ⋮ 8 hay A ⋮ 8

Vậy A chia hết cho 80.

Câu 46:

Cho góc $\hat{A O B}$ và góc $\hat{B O C}$ là hai góc kề bù. Biết góc $\hat{B O C}$ bằng năm lần góc $\hat{A O B}$ .

a) Tính số đo mỗi góc.

b) Gọi OD là tia phân giác của góc $\hat{B O C}$ . Tính số đo góc $\hat{A O D}$ .

c) Trên cùng nửa mặt phẳng bờ là đường thẳng AC chứa tia OB, OD, vẽ thêm n tia phân biệt (không trùng với các tia OA; OB; OC; OD đã cho) thì có tất cả bao nhiêu góc?

Cho góc AOB và góc BOC là hai góc kề bù. Biết góc BOC bằng năm (ảnh 1)

Câu 47:

Điền chữ số vào dấu * để:

a) $\bar{* 45 *}$ chia hết cho cả 2, 3, 5 và 9.

b) $\bar{21 *}$ chia hết cho cả 3 và 5.

Điền chữ số vào dấu * để: (ảnh 1)

Câu 48:

Điền chữ số vào dấu * để:

a) $\bar{6 * 7}$ chia hết cho 3.

b) $\bar{1 * 8}$ chia hết cho 9.

a) Để $\bar{6 * 7}$ chia hết cho 3 thì (6 + * + 7) ⋮ 3 hay (13 + *) ⋮ 3

Suy ra: * = 2; 5; 8

Vậy số cần tìm là 627, 657, 687.

b) Để $\bar{1 * 8}$ chia hết cho 9 thì (1 + * + 8) ⋮ 9 hay (9 + *) ⋮ 9

Suy ra: * = 0; 9

Vậy số cần tìm là 108, 198.

Câu 49:

Viết chữ số thích hợp vào ô trống để được: 1…8 chia hết cho 9.

Để 1…8 chia hết cho 9 thì (1 + 8 + … ) chia hết cho 9 hay (9 + …) chia hết cho 9.

Vậy ta cần viết vào ô trống một trong các chữ số 0 hoặc 9.

Câu 50:

Cho hình vuông ABCD có cạnh 14cm (hình bên). Như vậy, phần tô đen trong hình vuông ABCD có diện tích là?

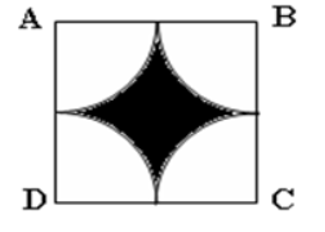
Cho hình vuông ABCD có cạnh 14cm (hình bên). Như vậy, phần tô đen trong (ảnh 1)

4 phần không tô đen nằm trong hình vuông ABCD ghép lại thành 1 hình tròn có bán kính 7cm.

Diện tích phần tô đen là:

14.14 – 3,14.7² = 42,14 (cm²).

Câu 51:

Một lớp học có 20 học sinh nam và 24 học sinh nữ. Có thể chia lớp đó thành nhiều nhất bao nhiêu tổ để số nam và số nữ được chia đều vào các tổ? Khi đó mỗi tổ có bao nhiêu nam, bao nhiêu nữ?

Gọi số tổ chia được nhiều nhất là a (a ∈ ℕ^*)

Vì lớp học có 20 học sinh nam và 24 học sinh nữ chia thành các tổ để số nam và số nữ được chia đều

⇒ 24 chia hết cho a; 20 chia hết cho a

⇒ a ∈ ƯC(20, 24)

Vì số tổ chia thành nhiều nhất nên a = ƯCLN(20, 24)

Ta có: 20 = 2².5

24 = 2³.3

⇒ ƯCLN(20, 24) = 2² = 4

Vậy số tổ chia được nhiều nhất là 4 tổ

Khi đó số nữ ở mỗi tổ là:

24 : 4 = 6 (học sinh)

Khi đó số nam ở mỗi tổ là:

20 : 4 = 5 (học sinh).

Câu 52:

Một phòng học hình chữ nhật có chiều dài 15m và chiều rộng 7m. Người ta mua loại gạch hình vuông có cạnh 0,5m để lát nền toàn bộ phòng học. Tính số viên gạch cần dùng để lát đủ phòng học đó.

Diện tích phòng học là:

15.7 = 105 (m²)

Diện tích viên gạch hình vuông là:

0,5 . 0,5 = 0,25 (m²)

Số viên gạch cần dùng là:

105 : 0,25 = 420 (viên)

Câu 53:

Để lát nền một căn phòng hình chữ nhật có chiều dài 27m, chiều rộng 15m, Người ta cần dùng một số viên gạch hình vuông có cạnh 30cm. Số viên gạch cần dùng là?

Diện tích nền căn phòng là: 27.15 = 405 (m²) = 4050000 cm²
Diện tích 1 viên gạch là: 30.30 = 900 (cm²)

Số viên gạch cần dùng là: 4050000 : 900 = 4500 (viên gạch)

Đáp số: 4500 viên gạch

Câu 54:

Tìm tập xác định $\tan (x - \frac{π}{4})$ .

Hàm số xác định khi $\cos (x - \frac{π}{4}) \neq 0 \Leftrightarrow x - \frac{π}{4} \neq \frac{π}{2} + k π \Leftrightarrow x \neq \frac{3 π}{4} + k π (k \in ℤ)$ .

Câu 55:

Cho $\sin α + \cos α = \frac{1}{2}$ . Tính sin2α, cos2α, tan2α, cot2α.

Cho sin alpha + cos alpha =1/2 . Tính sin2α, cos2α, tan2α, cot2α. (ảnh 1)

Câu 56:

Chứng minh $1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ .

$1 + \tan^{2} α = 1 + \frac{\sin^{2} α}{\cos^{2} α} = \frac{\cos^{2} α + \sin^{2} α}{\cos^{2} α} = \frac{1}{\cos^{2} α}$

Câu 57:

Tính giá trị đúng của $\tan \frac{π}{24} + \tan \frac{7 π}{24}$ .

Với 2 góc a và b thỏa mãn: cos a ≠ 0 và cos b ≠ 0 ta có $\tan a + \tan b = \frac{\sin a}{\cos a} + \frac{\sin b}{\cos b} = \frac{\sin a . \cos b + \sin b . \cos a}{\cos a . \cos b} = \frac{\sin (a + b)}{\cos a . \cos b}$

Áp dụng ta có: $\tan \frac{π}{24} + \tan \frac{7 π}{24} = \frac{\sin \frac{π}{3}}{\cos \frac{π}{24} . \cos \frac{7 π}{24}} = \frac{\sqrt{3}}{\cos \frac{π}{3} + \cos \frac{π}{4}} = 2 (\sqrt{6} - \sqrt{3})$ .

Câu 58:

Phương trình $t a n x + t a n (x + \frac{π}{3}) + t a n (x + \frac{2 π}{3}) = 3 \sqrt{3}$ tương đương với phương trình nào?

Phương trình tan x + tan( x +pi/3) + tan( x + 2pi/ 3) = 3 căn 3 tương đương với phương trình nào? (ảnh 2)

Câu 59:

Tìm tập xác định của hàm số y = tanx – cot2x.

Điều kiện xác định:

$\{\begin{cases} \sin 2 x \neq 0 \\ \cos x \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} 2 x \neq k π \\ x \neq \frac{π}{2} + k π \end{cases} \Leftrightarrow \{\begin{cases} x \neq \frac{k π}{2} \\ x \neq \frac{π}{2} + k π \end{cases} \Leftrightarrow x \neq \frac{k π}{2} (k \in ℤ)$ .

Vậy tập xác định $D = ℝ \ \{\frac{k π}{2}\}, k \in ℤ$ .

Câu 60:

Tìm 6 chữ số khác nhau a, b, c, d, e, g sao cho $A = \bar{a b c} - \bar{\deg}$ có giá trị nhỏ nhất.

Tìm 6 chữ số khác nhau a, b, c, d, e, g sao cho (ảnh 1)

Câu 61:

Biết hàm số bậc hai y = ax² + bx + c có đồ thị là một đường parabol đi qua điểm A(-1; 0) và có đỉnh B(1; 2). Khi đó, giá trị biểu thức T = a + b + c bằng bao nhiêu?

(P) đi qua A(-1; 0) nên: 0 = a – b + c

⇔ c = b - a (1)

(P) đi qua đỉnh B(1; 2) nên:

2 = a + b + c

Vậy T = a + b + c = 2.

Câu 62:

Viết công thức tổng quát nhân xác suất P(A.B.C) trong trường hợp A, B, C độc lập với nhau

P(A.B.C) = P(A).P(B).P(C).

Câu 63:

Tìm a và b biết C = $\bar{20 a 4 b}$ chia hết cho 45.

C chia hết cho 45 tức là C chia hết cho 5 và 9.

Để C chia hết cho 5 thì b = 0 hoặc b = 5.

Với b = 0 ta có số $\bar{20 a 40}$

Để $\bar{20 a 40}$ chia hết cho 9 thì (2 + 0 + a + 4 + 0) chia hết cho 9 hay (8 + a) chia hết cho 9.

Suy ra: a = 1

Vậy ta có số 20140.

Với b = 5 ta có số $\bar{20 a 40}$

Để $\bar{20 a 40}$ chia hết cho 9 thì (2 + 0 + a + 4 + 5) chia hết cho 9 hay (11 + a) chia hết cho 9.

Suy ra: a = 7.

Vậy ta có số 20745.

Câu 64:

Tính tổng A = 1 + 2 + 3 + … + 100.

A = 1 + 2 + 3 + … + 100

A = (1 + 100) + (2 + 99) + ….

Từ 1 đến 100 có 100 số. Như vậy, số cặp số là:

100: 2 = 50 (cặp)

Mỗi cặp số có tổng bằng:

1 + 100 = (2 + 99) = (3 + 98)... = 101

Kết quả của phép tính là:

101.50 = 5050

Đáp số: 5050.

Câu 65:

Tính tổng dãy số 1 + 2 + 3 + 4 + … + 99.

Ta thấy các số hạng hơn kém nhau 1 đơn vị

Số các số hạng của dãy là:

(99 – 1) : 1 + 1 = 99 (số hạng)

Tổng dãy số là:

(1 + 99).99 : 2 = 4950.

Câu 66:

Với 5 chữ số 1,2,3,4,5 ta có thể viết được bao nhiêu số có: ba chữ số mà các chữ số có thể được lặp lại.

Có 5 cách chọn chữ số hàng trăm, có 5 cách chọn chữ số hàng chục và có 5 cách chọn chữ số hàng đơn vị.

Vậy có tất cả: 5.5.5 = 125 (số)

Câu 67:

So sánh $\frac{2008}{2009} + \frac{2009}{2010} + \frac{2010}{2011} + \frac{2011}{2008}$ và 4.

So sánh 2008/ 2009 + 2009/2010 + 2010/2011 + 2011/ 2008 và 4. (ảnh 1)

Câu 68:

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số $y = \frac{1}{3} x^{3} - x^{2} + (m - 1) x + 2$ có hai điểm cực trị đều nằm bên trái trục tung.

A. 1 < m < 2.

B. m > 1.

C. m < 2.

D. m < 1.

Chọn A.

Ta có: y’ = x² – 2x + m – 1

Đồ thị hàm số có 2 điểm cực trị đều nằm bên trái trục tung khi y ' = 0 có 2 nghiệm phân biệt đều dương

⇔ Δ ' = 1 − m + 1 > 0

S = 2 > 0

P = m − 1 > 0

(trong đó S là tổng 2 nghiệm và P là tích 2 nghiệm của phương trình)

⇔ 2 > m > 1.

Câu 69:

Cho A = 1 + 2 + 2² + … + 2⁵⁰. Hãy chứng tỏ A + 1 là một lũy thừa của 2.

A = 1 + 2 + 2² + … + 2⁵⁰

2A = 2 + 2² + … + 2⁵¹

2A – A = (2 + 2² + … + 2⁵¹) – (1 + 2 + 2² + … + 2⁵⁰)

A = 2⁵¹ – 1

Suy ra: A + 1 = 2⁵¹ (đpcm)

Vậy A + 1 là một lũy thừa của 2.

Câu 70:

Tính giá trị biểu thức A = 1 + 2 + 3 + … + 2011.

Ta thấy các số hạng hơn kém nhau 1 đơn vị

Số các số hạng của dãy số A là:

(2011 – 1) : 1 + 1 = 2011

Giá trị của dãy số A là:

(1 + 2011) . 2011 : 2 = 2023066.

Câu 71:

Tính nhanh 1 + 2 + 3 + … + 59 + 60.

Ta thấy các số hạng hơn kém nhau 1 đơn vị

Số các số hạng của dãy số A là:

(60 – 1) : 1 + 1 = 60

Giá trị của dãy số A là:

(1 + 60) . 60 : 2 = 1830.

Câu 72:

Một căn phòng hình chữ nhật có chiều dài 8m, chiều rộng bằng $\frac{3}{4}$ chiều dài. Để lát nền căn phòng đó. Người ta dùng loại gạch men hình vuông cạnh 4dm.

a) Hỏi căn phòng được lát cần bao nhiêu viên gạch đó.

b) Biết rằng để lát 1m² gạch men hết 75000 đồng. Vậy để lát hết căn phòng đó thì hết bao nhiêu tiền?

a) Chiều rộng căn phòng là:

$8. \frac{3}{4} = 6 (m)$

Diện tích căn phòng là:

8.6 = 48 (m²) = 4800 dm²

Diện tích mỗi viên gạch là:

4.4 = 16 (dm²)

Cần số viên gạch là:

4800 : 16 = 300 (viên)

b) Lát hết căn phòng đó cần số tiền là:

75000 . 48 = 3600000 (đồng).

Câu 73:

Cho hệ phương trình $\{\begin{cases} x + m y = 2 \\ m x - 2 y = 1 \end{cases}$ .

Tìm các số nguyên m để hệ có nghiệm duy nhất (x; y) mà x; y là các số nguyên.

Cho hệ phương trình x + my = 2; mx -2y= 1 (ảnh 2)

Câu 74:

Tìm x biết (2x – 3)² = 9.

(2x – 3)² = 9

⇔ $[\begin{array}{l} 2 x - 3 = 3 \\ 2 x - 3 = - 3 \end{array}$

⇔ $[\begin{array}{l} x = 3 \\ x = 0 \end{array}$

Vậy x = 0 hoặc x = 3.

Câu 75:

Rút gọn (3x + 2)(3x – 2).

(3x + 2)(3x – 2)

= (3x)² – 2²

= 9x² – 4.

Câu 76:

Tìm x biết (3x – 2⁴).7³ = 2.7⁴.

(3x – 2⁴).7³ = 2.7⁴

⇔ (3x – 16).343 = 4802

⇔ 3x – 16 = 14

⇔ 3x = 30

⇔ x = 10.

Vậy x = 10.

Câu 77:

Cho hình vuông ABCD. Tính giá trị $(\vec{A B} + \vec{A C} + \vec{A D}) (\vec{D A} + \vec{D B} + \vec{D C})$ .

Cho hình vuông ABCD. Tính giá trị (ảnh 1)

Câu 78:

Tính $\sqrt{2 - \sqrt{3}} . (\sqrt{6} + \sqrt{2})$ .

Tính căn 2 - căn 3 ( căn 6 + căn 2) . (ảnh 1)

Câu 79:

Rút gọn biểu thức $P = (\frac{8 - x \sqrt{x}}{2 - \sqrt{x}} + 2 \sqrt{x}) {(\frac{2 - \sqrt{x}}{2 + \sqrt{x}})}^{2}$ .

Rút gọn biểu thức P= (8 - x căn x/ 2 - căn x + 2 căn x) ( 2 - căn x/ 2 + căn x)^2 . (ảnh 1)

Câu 80:

Tìm x biết (x + 7)(2x – 6) = 0.

(x + 7)(2x – 6) = 0

⇔ $[\begin{array}{l} x + 7 = 0 \\ 2 x - 6 = 0 \end{array}$

⇔ $[\begin{array}{l} x = - 7 \\ x = 3 \end{array}$

Vậy x = -7 hoặc x = 3.

Câu 81:

Cho 2 số x,y thỏa mãn đẳng thức $(x + \sqrt{x^{2} + 2020}) (y + \sqrt{y^{2} + 2020}) = 2020$ . Tính x + y.

Cho 2 số x,y thỏa mãn đẳng thức ( x + căn x^2 + 2020) ( y + căn y^2 + 2020) = 2020. Tính x + y (ảnh 1)

Câu 82:

Chứng minh rằng $\frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} + 4 \geq 3 (\frac{x}{y} + \frac{y}{x})$ .

Chứng minh rằng x^2 /y^2 + y^2/ x^2 + 4 lớn hơn hoặc bằng 3( x/y + y/x) . (ảnh 1)

Câu 83:

Tìm x biết x² – 4 + (x – 2)(3 – 2x) = 0.

(x² – 4) + (x – 2)(3 – 2x) = 0

⇔ (x – 2)(x + 2) + (x – 2)(3 – 2x) = 0

⇔ (x – 2)[(x + 2) + (3 – 2x)] = 0

⇔ (x – 2)(5 – x) = 0

⇔ x – 2 = 0 hoặc 5 – x = 0

+ x – 2 = 0 ⇔ x = 2

+ 5 – x = 0 ⇔ x = 5.

Vậy tập nghiệm của phương trình là S = {2; 5}.

Câu 84:

Khai triển biểu thức (–x – 3y)³ ta được?

(–x – 3y)³ = [–(x + 3y)]³ = –x³ – 9x²y – 27xy² – 27y³.

Câu 85:

Rút gọn biểu thức (x – y + z)² + (z – y)² + 2(x – y + z)(y – z).

(x – y + z)² + (z – y)² + 2(x – y + z)(y – z)

= (x – y + z)² + 2(x – y + z)(y – z) + (z – y)²

= (x – y + z + y – z)²

= x².

Câu 86:

Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0.

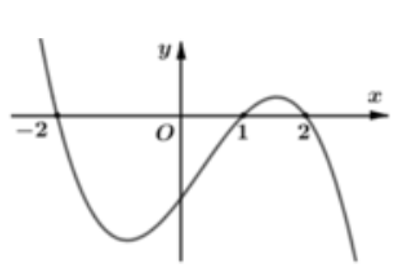
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0. (ảnh 1)

Hàm số g( x) = [f(3 - x)]² nghịch biến trên khoảng nào trong các khoảng sau?

A. (- 2; -1).

B. (1; 2).

C. (2; 5).

D. ( 5 ; +∞).

Chọn C.

Dựa vào đồ thị hàm số y = f’(x) suy ra bảng biến thiên của hàm số y = f(x)

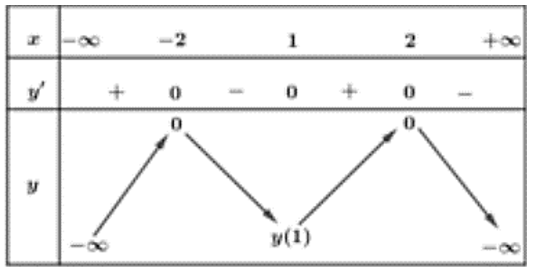
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0. (ảnh 2)

Suy ra: f(x) ≤ 0 với mọi x

Ta có: g’(x) = -2f’(3 – x).f(3 – x)

Xét g’(x) < 0 thì f’(3 – x).f(3 – x) > 0

⇔ $\{\begin{cases} f' (3 - x) < 0 \\ f (3 - x) < 0 \end{cases} \Leftrightarrow \{\begin{cases} - 2 < 3 - x < 1 \\ 3 - x > 2 \end{cases} \Leftrightarrow \{\begin{cases} 2 < x < 5 \\ x < 1 \end{cases}$

Suy ra hàm số y = g(x) nghịch biến trên các khoảng (2; 5) và (-∞; 1).

Câu 87:

Một khu rừng hình chữ nhật có chu vi 7km 5 hm, chiều rộng bằng $\frac{2}{3}$ chiều dài. Tính diện tích khu rừng đó với đơn vị đo là mét vuông, là héc-ta.

7km 5hm = 7500m

Nửa chu vi khu rừng là:

7500 : 2 = 3750 (m)

Chiều rộng khu rừng là:

3750 : (2 + 3) . 2 = 1500 (m)

Chiều dài khu rừng là:

3750 : (2 + 3) . 3 = 2250 (m)

Diện tích khu rừng là:

1500.2250 = 3375000 (m²) = 337,5ha

Vậy diện tích khu rừn rừng là 3375000m² = 337,5ha.

Bắt đầu thi ngay

Bài thi liên quan