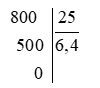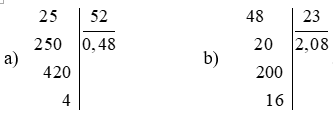- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 63)
-
13049 lượt thi
-
131 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
(4x – 3)2 – 3x(3 – 4x) = 0
⇔ (3 – 4x)2 – 3x(3 – 4x) = 0
⇔ (3 – 4x)(3 – 4x – 3x) = 0
⇔ (3 – 4x)(3 – 7x) = 0
⇔ \(\left[ \begin{array}{l}3 - 4x = 0\\3 - 7x = 0\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = \frac{3}{4}\\x = \frac{3}{7}\end{array} \right.\)
Vậy phương trình có tập nghiệm là: \(S = \left\{ {\frac{3}{4};\frac{3}{7}} \right\}.\)
Câu 2:
Rút gọn phân thức: \(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\).
 Xem đáp án
Xem đáp án
\(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\)
\( = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)\left( {x - 5} \right)\left( {x + 5} \right)}}{{\left( {x + 2} \right)\left( {x + 5} \right)}}\)
= (x + 1)(x – 5)
= x2 – 4x – 5.
Câu 3:
Giải phương trình: 2x2 + 5x – 3 = 0.
 Xem đáp án
Xem đáp án
2x2 + 5x – 3 = 0
⇔ 2x2 – 6x + x – 3 = 0
⇔ 2x(x – 3) + (x – 3) = 0
⇔ (2x – 1)(x + 3) = 0
⇔ \(\left[ \begin{array}{l}x = \frac{1}{2}\\x = - 3\end{array} \right.\)
Vậy phương trình có nghiệm là x = –3 hoặc \(x = \frac{1}{2}.\)
Câu 4:
Cho đường tròn (O). Từ điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến ME, MF. Biết OE = 3 cm, OM = 5 cm.
a) Tính độ dài EF.
b) Tính chu vi và diện tích tam giác MEF.
 Xem đáp án
Xem đáp án
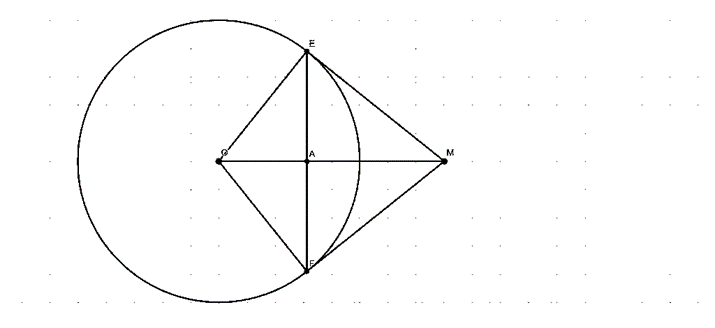
a) OM ∩ EF = {A}
OE = OF = R
ME = MF (tính chất tiếp tuyến)
Suy ra: MO là đường trung trực của EF
⇒ EA ⊥ OM; 2EA = EF
Xét ΔOEM vuông tại E có đường cao EA, có:
OE2 + ME2 = OM2
32 + ME2 = 52
ME2 = 25 – 9 = 16
ME = 4 (cm)
Lại có: \(\frac{1}{{E{A^2}}} = \frac{1}{{E{O^2}}} + \frac{1}{{E{M^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} = \frac{{25}}{{144}}\)
Suy ra: EA = \(\frac{{12}}{5}\left( {cm} \right) \Rightarrow EF = 2EA = \frac{{24}}{5}\)(cm)
b) PMEF = ME + MF + EF = 2ME + EF = \(2.4 + \frac{{24}}{5} = \frac{{64}}{5}\left( {cm} \right)\)
Xét tam giác OEM vuông tại E có đường cao EA có:
EM2 = MA.MO
AM = \(\frac{{E{M^2}}}{{MO}} = \frac{{{4^2}}}{5} = \frac{{16}}{5}\)
SMEF = \(\frac{1}{2}.AM.EF = \frac{1}{2}.\frac{{16}}{5}.\frac{{24}}{5} = \frac{{192}}{{25}}\left( {c{m^2}} \right)\).
Câu 5:
Tam giác ABC có a = 5, b = 4, c = 3. Lấy điểm D đối xứng B qua C. Độ dài đoạn AD.
 Xem đáp án
Xem đáp án
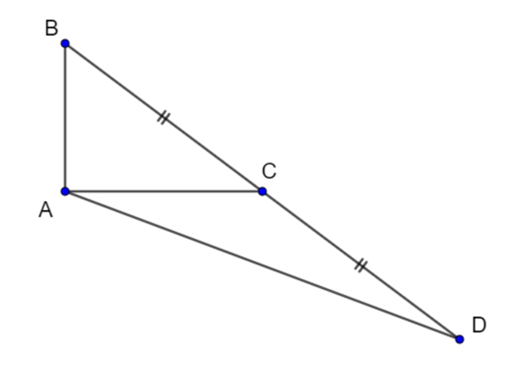
a = 5; b = 4; c = 3 ⇒ BC = 5; AC = 4; AB = 3
D đối xứng với B qua C ⇒ C là trung điểm của BD
⇒ \(BC = \frac{1}{2}BD \Rightarrow BD = 2BC = 2.5 = 10\)
Xét tam giác ADB có AC là đường trung tuyến
⇒ \(A{C^2} = \frac{{2\left( {A{B^2} + A{D^2}} \right) - B{D^2}}}{4}\)
⇔ \({4^2} = \frac{{2\left( {{3^2} + A{D^2}} \right) - {{10}^2}}}{4}\)
⇔ 18 + 2AD2 – 100 = 64
⇔ AD2 = 73
⇔ \(AD = \sqrt {73} \).
Câu 6:
Tìm điều kiện xác định của hàm số: \(y = \frac{1}{{\sin x - \cos x}}\).
 Xem đáp án
Xem đáp án
Điều kiện xác định: sinx – cosx ≠ 0
⇔ \(\sin \left( {x - \frac{\pi }{4}} \right) \ne 0\)
⇔ \(x \ne \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Câu 7:
Cho \(P = \left( {\frac{1}{{\sqrt x }} + \frac{{\sqrt x }}{{\sqrt x + 1}}} \right):\frac{{\sqrt x }}{{x + \sqrt x }}\).
a) Rút gọn P.
b) Tìm giá trị của P khi x = 4.
c) Tìm x để \(P = \frac{{13}}{3}\).
 Xem đáp án
Xem đáp án
a) Điều kiện: x > 0
\(P = \left( {\frac{1}{{\sqrt x }} + \frac{{\sqrt x }}{{\sqrt x + 1}}} \right):\frac{{\sqrt x }}{{x + \sqrt x }}\)
\(P = \left( {\frac{{\sqrt x + 1 + x}}{{\sqrt x \left( {\sqrt x + 1} \right)}}} \right):\frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)}}\)
\(P = \frac{{\sqrt x + 1 + x}}{{\sqrt x \left( {\sqrt x + 1} \right)}}.\frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x }}\)
\(P = \frac{{\sqrt x + 1 + x}}{{\sqrt x }}\)
b) Thay x = 4 vào ta có: \(P = \frac{{\sqrt 4 + 1 + 4}}{{\sqrt 4 }} = \frac{{2 + 1 + 4}}{2} = \frac{7}{2}\)
c) Khi \(P = \frac{{13}}{3}\) thì \(\frac{{13}}{3} = \frac{{\sqrt x + 1 + x}}{{\sqrt x }}\)
⇔ \(3x + 3\sqrt x + 3 = 13\sqrt x \)
⇔ \(3x - 10\sqrt x + 3 = 0\)
⇔ \(3x - 9\sqrt x - \sqrt x + 3 = 0\)
⇔ \(\sqrt x \left( {3\sqrt x - 1} \right) - 3\left( {3\sqrt x - 1} \right) = 0\)
⇔ \(\left( {\sqrt x - 3} \right)\left( {3\sqrt x - 1} \right) = 0\)
⇔ \(\left[ \begin{array}{l}\sqrt x - 3 = 0\\3\sqrt x - 1 = 0\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = 9\\x = \frac{1}{9}\end{array} \right.\).
Câu 8:
Gọi x0 là nghiệm âm lớn nhất của \[\sin 9x + \sqrt 3 \cos 7x = \sin 7x + \sqrt 3 \cos 9x\]. Tìm x0?
 Xem đáp án
Xem đáp án
\[\sin 9x + \sqrt 3 \cos 7x = \sin 7x + \sqrt 3 \cos 9x\]
⇔ \[\sin 9x - \sqrt 3 \cos 9x = \sin 7x - \sqrt 3 \cos 7x\]
⇔ \(\sin \left( {9x - \frac{\pi }{3}} \right) = \sin \left( {7x - \frac{\pi }{3}} \right)\)
⇔ \(\left[ \begin{array}{l}9x - \frac{\pi }{3} = 7x - \frac{\pi }{3} + k2\pi \\9x - \frac{\pi }{3} = \pi - \left( {7x - \frac{\pi }{3}} \right) + k2\pi \end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = k\pi \\x = \frac{{5\pi }}{{48}} + k\frac{\pi }{8}\end{array} \right.\)
Cho x < 0 ta được:
\(\left[ \begin{array}{l}k\pi < 0\\\frac{{5\pi }}{{48}} + k\frac{\pi }{8} < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}k < 0\\k < \frac{{ - 5}}{6}\end{array} \right.\left( {k \in \mathbb{Z}} \right) \Rightarrow \left[ \begin{array}{l}{k_{\max }} = - 1\\{k_{\max }} = - 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = - \pi \\x = - \frac{\pi }{{48}}\end{array} \right.\)
So sánh hai nghiệm âm trên ta được nghiệm âm lớn nhất của phương trình là \(x = \frac{{ - \pi }}{{48}}\)
Vậy \({x_0} = \frac{{ - \pi }}{{48}}\).
Câu 9:
Hai người đi xe từ A đến C. Người thứ nhất đi theo đường từ A đến B rồi từ B đến C. Người thứ hai đi thẳng từ A đến C. Cả hai đều về đích cùng lúc. Tính quãng đường và độ dịch chuyển của người thứ nhất và người thứ hai, so sánh và nhận xét kết quả biết ABC tạo thành tam giác vuông 1 tam giác vuông.
 Xem đáp án
Xem đáp án
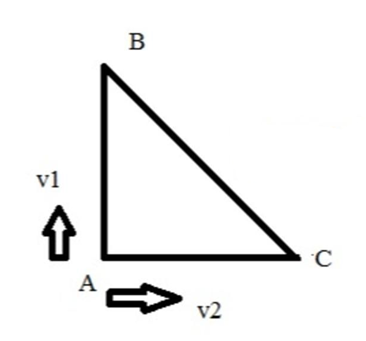
Theo bất đẳng thức tam giác ta có tổng độ dài hai cạnh bất kỳ lớn hơn độ dài cạnh còn lại. Ta có: AB + BC > AC
Mà s1 = AB + BC
s2 = AC
⇒ s1 > s2
Lại có cả hai đến đích cùng lúc, do đó v1 > v2 (do thời gian bằng nhau).
Câu 10:
Từ một tổ gồm 5 bạn nam và 4 bạn nữ. chọn ngẫu nhiên 5 bạn xếp thành 1 hàng ngang. tính xác suất sao cho trong những cách xếp trên có đúng 3 bạn nam.
 Xem đáp án
Xem đáp án
Chọn ngẫu nhiên 5 bạn từ một tổ gồm 9 bạn và xếp thành một hàng ngang có \(A_9^5 = 15120\)cách
Suy ra số phần tử của không gian mẫu là n(Ω) = 15120
Gọi A là biến cố "Có đúng 3 bạn nam"
Chọn 3 nam trong 5 bạn nam và 2 nữ trong 4 bạn nữ và xếp thành một hàng ngang có 5!.\(C_5^3.C_4^2\) = 7200 cách.
Suy ra số kết quả thuận lợi cho biến cố A là n(A) = 7200
Vậy xác suất sao cho trong những cách xếp trên có đúng 3 bạn nam là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{7200}}{{15120}} = \frac{{10}}{{21}}\).
Câu 12:
Tìm 1 số tự nhiên có 4 chữ số biết rằng khi viết thêm chữ số 7 vào bên phải số đó thì được số lớn hơn số phải tìm 11212 đơn vị.
 Xem đáp án
Xem đáp án
Số tự nhiên có 4 chữ số khi viết thêm chữ số 7 vào bên phải số đó, thì số đó gấp lên 10 lần và tăng thêm 7 đơn vị
Ta có sơ đồ như hình vẽ
Từ sơ đồ ta thấy 9 phần số cần tìm là:
11212 – 7 = 11205 (đơn vị)
Số phải tìm là:
11205 : 9 = 1245
Đáp số: 1245.
Câu 13:
Nêu quy tắc tính xác suất của sự kiện A1, A2, ….,Ak: P(A1 ∪ A2 ∪ … ∪ Ak).
 Xem đáp án
Xem đáp án
Ta áp dụng quy tắc cộng xác suất khi k biến cố A1, A2, …, Ak đôi một xung khắc, xác suất để ít nhất một trong các biến cố A1, A2, …, Ak xảy ra là:
P(A1 ∪ A2 ∪ … ∪ Ak) = P(A1) + P(A2) + … + P(Ak).
Câu 14:
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Tính độ lớn và hướng vận tốc tổng hợp của vận động viên?
 Xem đáp án
Xem đáp án
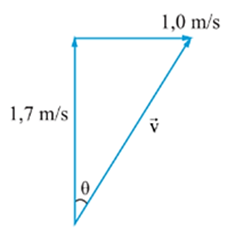
Độ lớn vận tốc tổng hợp của vận động viên là:
\(\overrightarrow v \)tổng hợp = \(\overrightarrow v \) + \(\overrightarrow v \)nước
Suy ra: vtổng hợp = \(\sqrt {{v^2} + {v_{nuoc}}^2} = \sqrt {1,{7^2} + {1^2}} = 1,97\left( {m/s} \right)\)
Hướng vận tốc tổng hợp của vận động viên hợp với bờ sông 1 góc là:
\(\tan \alpha = \frac{v}{{{v_{nuoc}}}} = \frac{{1,7}}{1} = 1,7 \Rightarrow \alpha \approx 59,53^\circ \)
Câu 15:
Xét tính chẵn, lẻ của hàm số y = f(x) = \(\sin \left( {2x + \frac{{9\pi }}{2}} \right)\).
 Xem đáp án
Xem đáp án
Tập xác định D = ℝ , là một tập đối xứng. Do đó ∀x ∈ D thì –x ∈ D
Ta có:
f(x) = \(\sin \left( {2x + \frac{{9\pi }}{2}} \right) = \sin \left( {2x + \frac{\pi }{2} + 4\pi } \right) = \sin \left( {2x + \frac{\pi }{2}} \right) = \cos 2x\)
f(–x) = cos(–2x) = cos2x = f(x)
Vậy hàm số f(x) là hàm số chẵn.
Câu 16:
 Xem đáp án
Xem đáp án
Hàm số có nghĩa khi \(\left\{ \begin{array}{l}\cos x \ne 0\\\sin x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{2} + k\pi \\x \ne l\pi \end{array} \right.\left( {k,l \in \mathbb{Z}} \right)\)
Tập xác định là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,;l\pi \left| {k,l \in \mathbb{Z}} \right.} \right\}\)tập đối xứng.
Do đó ∀x ∈ D thì –x ∈ D
Ta có f(−x) = tan(−x) + cot(−x) = −tanx – cotx = −(tanx + cotx) = −f(x).
Vậy f(x) là hàm số lẻ. Đồ thị hàm số nhận gốc tọa độ làm tâm đối xứng.
Câu 17:
Xếp 5 người A, B, C, D, E ngẫu nhiên vào 1 chiếc ghế có 5 chỗ ngồi. Tính xác suất để A ngồi chính giữa B và C.
 Xem đáp án
Xem đáp án
Có 1 cách xếp A chính giữa
B, C ngồi cạnh A; hoán vị có 2! Cách
Coi A, B, C thành 1 nhóm X
2 người còn lại hoán vị có 2! cách xếp.
Hoán vị nhóm X và 2 người còn lại có 3! cách
Xác suất A ngồi chính giữa B và C là: \(\frac{{1.2!.2!.2!.3!}}{{5!}} = \frac{1}{5}\).
Câu 18:
 Xem đáp án
Xem đáp án
Khi các số đo góc tính ra quá lẻ, chúng ta sẽ làm tròn độ, phút, giây tùy từng trường hợp.
Khi số phút vượt 30 độ thì ta +1 độ vào.
Ví dụ: 30 độ 32′ 4′′ thì làm tròn thành 31 độ.
Câu 19:
Cách bấm CALC arc lượng giác trên máy tsinh Casio 580fx–580VNX.
 Xem đáp án
Xem đáp án
Bấm Shift + sin, hoặc Shift + cos, Shift + tan

Sau đó: Bấm Alpha + )

Ta được hiển thị trên màn hình là: sin–1(X), cos–1(X),..
Sau đó bấm CALC nhập giá trị cần tính vào
Khi đó sẽ hiển thị số đo góc bạn cần tìm.
Câu 20:
Tìm GTLN, GTNN của hàm số \(y = \frac{{2\sin x + \cos x + 3}}{{2\cos x - \sin x + 4}}\).
 Xem đáp án
Xem đáp án
Tập xác định: 2cosx – sinx + 4 ≠ 0
Suy ra: x ∈ ℝ
Khi đó: y(2cosx – sinx + 4) = 2sinx + cosx + 3
⇔ (2y – 1)cosx – (y + 2)sinx = 3 – 4y (*)
Để (*) có nghiệm thì:
(3 – 4y)2 ≤ (2y – 1)2 + [–(y + 2)]2
⇔ \(\frac{2}{{11}} \le y \le 2\)
Từ đó suy ra: ymax = 2; ymin = \(\frac{2}{{11}}\).
Câu 21:
Giải phương trình: \(2{\sin ^2}\frac{x}{2} = \cos 5x + 1\).
 Xem đáp án
Xem đáp án
\(2{\sin ^2}\frac{x}{2} = \cos 5x + 1\)
⇔ \(2.\frac{{1 - \cos x}}{2} = \cos 5x + 1\)
⇔ 1 – cosx = cos5x + 1
⇔ cos5x + cosx = 0
⇔ 2cos3x cos2x = 0
⇔ \(\left[ \begin{array}{l}\cos 3x = 0\\\cos 2x = 0\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}3x = \frac{\pi }{2} + k\pi \\2x = \frac{\pi }{2} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\)
⇔ \(\left[ \begin{array}{l}x = \frac{\pi }{6} + k\frac{\pi }{3}\\x = \frac{\pi }{4} + k\frac{\pi }{2}\end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\).
Câu 22:
Phân tích đa thức thành nhân tử: 5x2 – 5xy – 10x + 10y.
 Xem đáp án
Xem đáp án
5x2 – 5xy – 10x + 10y
= 5(x2 –xy – 2x + 2y)
= 5[(x2 – xy) – (2x – 2y)]
= 5[x(x – y) – 2(x – y)]
= 5(x – y)(x – 2).
Câu 23:
Cho biểu thức: \(P = \left( {\frac{{x - y}}{{\sqrt x - \sqrt y }} + \frac{{\sqrt {{x^3}} - \sqrt {{y^3}} }}{{y - x}}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\) với x ≥ 0, y ≥ 0, x ≠ y.
a) Rút gọn A.
b) Chứng minh rằng A ≥ 0.
 Xem đáp án
Xem đáp án
a) Với x ≥ 0, y ≥ 0, x ≠ y. Ta có:
\(P = \left( {\frac{{x - y}}{{\sqrt x - \sqrt y }} + \frac{{\sqrt {{x^3}} - \sqrt {{y^3}} }}{{y - x}}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\)
\(P = \left( {\frac{{\left( {\sqrt x - \sqrt y } \right)\left( {\sqrt x + \sqrt y } \right)}}{{\sqrt x - \sqrt y }} + \frac{{\left( {\sqrt x - \sqrt y } \right)\left( {x + \sqrt {xy} + y} \right)}}{{y - x}}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\)
\(P = \left( {\sqrt x + \sqrt y - \frac{{\left( {\sqrt x - \sqrt y } \right)\left( {x + \sqrt {xy} + y} \right)}}{{\left( {\sqrt x - \sqrt y } \right)\left( {\sqrt x + \sqrt y } \right)}}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\)
\(P = \left( {\sqrt x + \sqrt y - \frac{{x + \sqrt {xy} + y}}{{\sqrt x + \sqrt y }}} \right):\frac{{{{\left( {\sqrt x - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x + \sqrt y }}\)
\[P = \frac{{{{\left( {\sqrt x + \sqrt y } \right)}^2} - x - \sqrt {xy} - y}}{{\sqrt x + \sqrt y }}.\frac{{\sqrt x + \sqrt y }}{{x - \sqrt {xy} + y}}\]
\[P = \frac{{\sqrt {xy} }}{{x - \sqrt {xy} + y}}\].
b) Ta có: x ≥ 0, y ≥ 0, x ≠ y thì \(\sqrt {xy} \ge 0\)
\[x - \sqrt {xy} + y = {\left( {\sqrt x - \sqrt y } \right)^2} + \sqrt {xy} \ge 0\]
Vậy A ≥ 0 với x ≥ 0, y ≥ 0, x ≠ y.
Câu 24:
 Xem đáp án
Xem đáp án
Giả sử số hạng đầu tiên là a.
Có thể thấy đây là cấp số cộng với công sai d = 2 (vì các số chẵn liên tiếp hơn kém nhau 2 đơn vị)
Tổng 13 số hạng đầu tiên là: 24 . 13 = 312
Ta có: 312 = \(\frac{{13}}{2}\left( {2a + 12.2} \right)\)
Suy ra: a = 12
Số hạng thứ 30 là: u30 = 12 + (30 – 1).2 = 70.
Câu 25:
Cho hàm số y = \(\frac{{x + 1}}{{x - 3}}\) có đồ thị (C) và các đường thẳng d1: y = 2x, d2: y = 2x – 2, d3: y = 3x + 3, d4: y = –x + 3. Hỏi có bao nhiêu đường thẳng trong 4 đường thẳng d1, d2, d3, d4 đi qua giao điểm của (C) và trục hoành.
 Xem đáp án
Xem đáp án
Gọi A là giao điểm của (C) và trục hoành ta có
A thuộc Ox nên yA = 0
Khi đó: x = –1
Suy ra: A(–1;0)
Thay A lần lượt vào d1, d2, d3, d4 có:
d1: –2 ≠ 0 (loại)
d2: –2 – 2 = –4 ≠ 0 (loại)
d3: –3 + 3 = 0 (thỏa mãn)
d4: 1 + 3 = 4 ≠ 0 (loại)
Vậy chỉ có 1 đường thẳng d3 đi qua giao điểm của (C) và trục hoành.
Câu 26:
Cho một số tự nhiên có 3 chữ số. Biết rằng thêm chữ số 3 vào bên phải số đó thì số đó tăng thêm 2892 đơn vị. Tổng các chữ số của số đó là?
 Xem đáp án
Xem đáp án
Khi viết thêm chữ số 3 vào bên phải một số thu được số mới gấp 10 lần số ban đầu và cộng thêm 3 đơn vị.
Nếu số ban đầu là 1 phần thì số mới là 10 phần cộng thêm 3 đơn vị.
Hiệu số phần bằng nhau là:
10 – 1 = 9 (phần)
Số đã cho là:
(2892 − 3) : 9 . 1 = 321
Tổng các chữ số của số đã cho là: 3 + 2 + 1 = 6.
Câu 27:
Cho nửa đường tròn (O) đường kính AB, tiếp tuyến Ax. Gọi C là một điểm trên nửa đường tròn. Tia phân giác của \(\widehat {CAx}\) cắt nửa đường tròn ở E, AE và BC cắt nhau ở K. AC cắt BE ở I.
a) Tam giác ABK là tam giác gì? Vì sao?
b) Chứng minh KI // Ax.
c) Chứng minh OE // BC.
 Xem đáp án
Xem đáp án
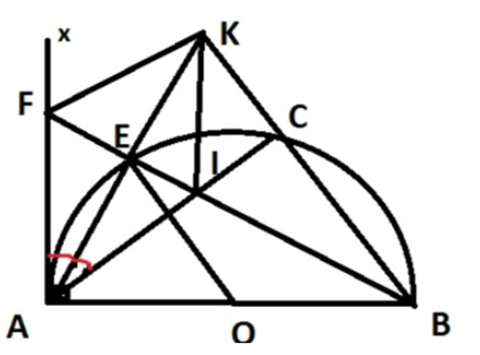
a) Ta có: Bx là phân giác của \(\widehat {ABC}\)nên BE là phân giác \(\widehat {ABK}\).
Vì AB là đường kính của (O)
⇒ BE ⊥ EA ⇒ BE ⊥ AK
⇒ ΔABK cân tại B
b) AB là đường kính của (O) ⇒ AC ⊥ BC
⇒ CA ⊥ BK
Mà BE ⊥ AK
⇒ I là trực tâm ΔKAB
⇒ KI ⊥ AB
⇒ KI // Ax
c) Ta có ΔBAK cân tại B, BE ⊥ AK
⇒ E là trung điểm AK
Lại có O là trung điểm AB
⇒ OE là đường trung bình ΔABK
⇒ OE // BK
⇒ OE // BC.
Câu 28:
Cho số A = 1.2.3.4…100
số B = 1000....00000.
Hỏi số B có nhiều nhất là bao nhiêu chữ số 0 biết A chia hết cho B.
 Xem đáp án
Xem đáp án
A = 1.2.3.4…100 = 100!
Từ 1 đến 100 có :
(100 – 10) : 10 + 1 = 10 (số hạng chia hết cho 10)
(100 – 2) : 2 + 1 = 50 (số hạng chia hết cho 2)
(100 – 5) : 5 + 1 = 20 (số chia hết cho 5)
⇒ Các số chia hết cho 2 không chia hết cho 10 là : 50 – 10 = 40 (số hạng)
⇒ Số chia hết cho 5 chia hết cho 10 là : 20 – 10 = 10 (số hạng)
Vì 10 < 40 ⇒ Tích giữa các số chỉ chia hết cho 2 với số chỉ chia hết cho 5 có 10 chữ số 0
mà có 10 số chia hết cho 10
⇒ A có 20 số 0 tận cùng
mà A chia hết cho B
⇒ B có 20 chữ số 0.
Câu 29:
Cho tam giác ABC vuông cân tại A,đường trung tuyến BM. Gọi D là hình chiếu của C trên BM, H là hình của D trên AC. Chứng minh rằng AH = 3HD.
 Xem đáp án
Xem đáp án
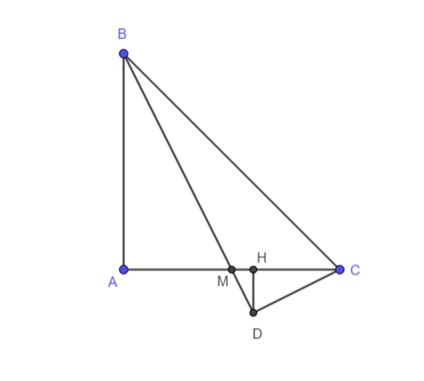
Đặt BA = CA = x
⇒ AM = MC = \(\frac{x}{2};BC = \sqrt 2 x\)
\(BM = \sqrt {B{A^2} + A{M^2}} = \frac{{\sqrt 5 x}}{2}\)
Xét △AMB và △DMC có:
\(\widehat A = \widehat H = 90^\circ \)
\(\widehat {AMB} = \widehat {HMD}\)
⇒ △AMB ∽ △DMC (g.g)
⇒ \(\frac{{MA}}{{MD}} = \frac{{MB}}{{MC}}\)
⇒ MA.MC = MB.MD
⇒ \(MD = \frac{{MA.MC}}{{MB}} = \frac{{x\sqrt 5 }}{{10}}\)
MD2 = MH.MC
⇒ \(MH = \frac{{M{D^2}}}{{DC}} = \frac{x}{{10}}\)
⇒ HC = MC – MH = \(\frac{{2x}}{5}\)
HD2 = HM.HC = \(\frac{x}{{10}}.\frac{{2x}}{5} = \frac{{{x^2}}}{{25}}\)
⇒ HD = \(\frac{x}{5}\)
HA = HM + MA = \(\frac{{3x}}{5}\)
⇒ HA = 3HD
Vậy HA = 3HD.
Câu 30:
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a) 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b) 3 điểm M, N, H thẳng hàng.
c) HA . HF = R2 – OH2.
 Xem đáp án
Xem đáp án
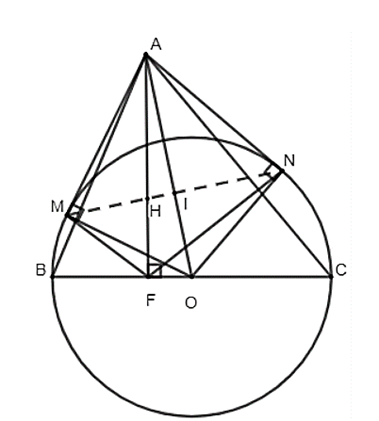
a) \(\widehat {AMO} = \widehat {AFO} = \widehat {ANO} = 90^\circ \)
⇒ A, M, F, N, O cùng thuộc một đường tròn
b) Gọi I là giao của MN và AO nên I là trung điểm của MN ⇒ AI.AO = AM2
Xét ∆AMH và ∆AFM có:
\(\widehat {MAH}\)chung
\(\widehat {AMH} = \widehat {AFM}\)
Nên ∆AMH ~ ∆AFM (g.g)
⇒ AH.AF = AM2 = AI.AO
⇒ \(\widehat {AHI} = \widehat {AOF}\)
⇒ OFHI nội tiếp
⇒ M, N, H thẳng hàng
c) Từ câu a) ta có: HM.HN = HA.HF
Ta có: HM.HN = (IM – IH).(IH + IN)
= (IM – IH).(IH + IM)
= IM2 – IH2
= OM2 – OI2 – (OH2 – OI2)
= R2 – OH2
Từ đó suy ra: HA.HF = R2 – OH2.
Câu 31:
Có 5 người trên 7 toa tàu được đánh số 1, 2, 3, 4, 5, 6, 7. Tính xác suất để 5 người lên 5 toa tàu khác nhau?
 Xem đáp án
Xem đáp án
Không gian mẫu n(Ω) = 75
Người thứ nhất có 7 cách chọn toa tàu.
Người thứ hai có 6 cách chọn toa tàu.
Người thứ ba có 5 cách chọn toa tàu.
Người thứ tư có 4 cách chọn toa tàu.
Người thứ năm có 3 cách chọn toa tàu.
Xác suất cần tìm là: \(\frac{{7.6.5.4.3}}{{{7^5}}} = \frac{{360}}{{2401}}\).
Câu 32:
Giải phương trình: \(\sqrt 3 \cos \left( {x + \frac{\pi }{2}} \right) + \sin \left( {x - \frac{\pi }{2}} \right) = 2\sin 2x\).
 Xem đáp án
Xem đáp án
\(\sqrt 3 \cos \left( {x + \frac{\pi }{2}} \right) + \sin \left( {x - \frac{\pi }{2}} \right) = 2\sin 2x\)
⇔ \( - \sqrt 3 \sin x - \cos x = 2\sin 2x\)
⇔ \(\sqrt 3 \sin x + \cos x = - 2\sin 2x\)
⇔ \(\frac{{\sqrt 3 }}{2}\sin x + \frac{1}{2}\cos x = - \sin 2x\)
⇔ \(\sin \left( {x + \frac{\pi }{6}} \right) = - \sin 2x = \sin \left( { - 2x} \right)\)
⇔ \[\left[ \begin{array}{l}x + \frac{\pi }{6} = - 2x + k2\pi \\x + \frac{\pi }{6} = \pi + 2x + k2\pi \end{array} \right.\]⇔ \[\left[ \begin{array}{l}x = - \frac{\pi }{{18}} + k\frac{{2\pi }}{3}\\x = - \frac{{5\pi }}{6} - k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\].
Câu 33:
Tính giá trị biểu thức M = cos215° + cos225° + cos235° + cos245° + cos2105° + cos2115° + cos2125°.
 Xem đáp án
Xem đáp án
M = cos215° + cos225° + cos235° + cos245° + cos2105° + cos2115° + cos2125°
M = (cos215° + sin215°) + (cos235° + sin235°) + (cos225° + sin225°) + cos245°
M = \(1 + 1 + 1 + \frac{1}{2} = \frac{7}{2}\).
Câu 34:
Một ca nô chạy trong hồ nước yên lặng có vận tốc tối đa 18 km/h. Nếu ca nô chạy ngang một con sông có dòng chảy theo hướng Bắc – Nam với vận tốc lên tới 5 m/s thì vận tốc tối đa nó có thể đạt được so với bờ sông là bao nhiêu và theo hướng nào?
 Xem đáp án
Xem đáp án
Gọi v13 là vận tốc của ca nô so với bờ sông, v23 là vận tốc của nước so với bờ, v12 là vận tốc của ca nô so với dòng nước.
Đổi v = 18 km/h = 5 m/s
Ca nô sẽ đi theo hướng Đông Nam so với bờ sông với vận tốc tối đa nó có thể đạt được là:
\({v_{13}} = \sqrt {{v_{12}}^2 + {v_{23}}^2} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \left( {m/s} \right)\).
Câu 35:
Một đơn vị bộ đội chuẩn bị 768kg lương thực đủ cho 80 người ăn trong 12 ngày luyện tập trước ngày tập trung quân ban chỉ huy báo về là số người sẽ tăng gấp 3 số dự kiến vậy để đủ ăn trong số ngày luyện tập như dự kiến đơn vị đó phải mua thêm số lương thực là bao nhiêu?
 Xem đáp án
Xem đáp án
Mỗi người ăn hết số kg lương thực trong 12 ngày là:
768 : 12 = 64 (kg)
Số người sau khi tăng lên gấp 3 của đơn vị là:
12 . 3 = 36 (người)
Số lương thực cần cho 36 người là:
36 . 64 = 2304 (kg)
Số lương thực cần mua thêm là:
2304 – 768 = 1536 (kg)
Đáp số: 1536 kg lương thực.
Câu 36:
Một đội công nhân 9 người trong một ngày đắp được 60 mét đường. Người ta bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được bao nhiêu mét đường đó (mức đắp mỗi người như nhau)?
 Xem đáp án
Xem đáp án
Số người công nhân hiện có là:
9 + 18 = 27 (người)
27 người đắp được số đoạn đường là:
\(\frac{{27}}{9}.60 = 180\left( m \right)\).
Câu 37:
Cho hệ phương trình: \[\left\{ \begin{array}{l}mx - y = 1\\my - x = m\end{array} \right.\].
Tìm giá trị m để hệ phương trình trên có nghiệm duy nhất.
 Xem đáp án
Xem đáp án
\[\left\{ \begin{array}{l}mx - y = 1\\my - x = m\end{array} \right.\]
⇔ \[\left\{ \begin{array}{l}y = mx - 1\\m\left( {mx - 1} \right) - x = m\end{array} \right.\]
⇔ \[\left\{ \begin{array}{l}y = mx - 1\\{m^2}x - m - x = m\end{array} \right.\]
⇔ \[\left\{ \begin{array}{l}y = mx - 1\\\left( {{m^2} - 1} \right)x = 2m\left( * \right)\end{array} \right.\]
Để hệ có nghiệm duy nhất thì (*) có nghiệm duy nhất khi và chỉ khi m2 – 1 khác 0
Hay m ≠ ±1.
Câu 38:
Cho số hữu tỉ \(x = \frac{{3a + 2}}{{ - 1}}\). Với giá trị nào của a thì x dương?
 Xem đáp án
Xem đáp án
x là số dương khi:
\(\frac{{3a + 2}}{{ - 1}} > 0\)
Suy ra: 3a + 2 < 0
⇒ 3a < –2
⇒ \(a < \frac{{ - 2}}{3}\)
Câu 39:
Xét tính chẵn lẻ của hàm số \(f\left( x \right) = \frac{{{{\sin }^{2020}}x + 2020}}{{\cos x}}\).
 Xem đáp án
Xem đáp án
Điều kiện xác định: \(D\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
Suy ra: D đối xứng
\(f\left( x \right) = \frac{{{{\sin }^{2020}}x + 2020}}{{\cos x}}\)
\(f\left( { - x} \right) = \frac{{{{\sin }^{2020}}\left( { - x} \right) + 2020}}{{\cos \left( { - x} \right)}}\)
\(f\left( { - x} \right) = \frac{{{{\left( { - \sin x} \right)}^{2020}} + 2020}}{{\cos x}}\)
\(f\left( { - x} \right) = \frac{{{{\sin }^{2020}}x + 2020}}{{\cos x}}\)
Vậy f(–x) = f(x)
Suy ra: f(x) là hàm chẵn.
Câu 40:
Cho dãy gồm 6 số nguyên tố phân biệt và tăng dần. Hiệu giữa hai số liên tiếp của dãy số đã cho đều bằng nhau. Chứng minh rằng hiệu giữa số lớn nhất và số bé nhất không nhỏ hơn 150.
 Xem đáp án
Xem đáp án
Gọi 6 số đó là p, p + d, p + 2d, p + 3d, p + 4d, p + 5d.
p + d, p + 2d là 2 số lẻ ⇒ hiệu ⋮ 2 (p + d ≥ 4)
p + d, p + 2d, p + 3d > 3 các số này ⋮̸ 3 nên có 2 số có cùng số dư khi chia 3.
Hiệu của chúng là d hoặc 2d ⋮ 3
⇒ d ⋮ 3
⇒ d ⋮ 6 nên d ≥ 6
p + d, p + 2d, p + 3d, p + 4d, p + 5d là 5 số, các số này không chia hết 5 nên có 2 số có cùng số dư khi chia 5.
Hiệu của chúng là d, 2d, 3d hoặc 4d ⋮ 5
⇒ d ⋮ 5
⇒ d ⋮ 30
Ta có : d ≥ 30
⇒ 5d ≥ 150 (đpcm)
Vậy hiệu giữa số lớn nhất và số bé nhất không nhỏ hơn 150.
Câu 41:
Tính giá trị biểu thức: 80 – (4.52 – 3.23).
 Xem đáp án
Xem đáp án
80 – (4.52 – 3.23)
= 80 – (4.25 – 3.8)
= 80 – (100 – 24)
= 80 – 76
= 4.
Câu 42:
Cho tam giác ABC có \(\widehat B = 60^\circ ,\widehat C = 45^\circ ,BC = a\).
a) Tính AB, AC.
b) Chứng minh \(\cos 75^\circ = \frac{{\sqrt 6 - \sqrt 2 }}{4}\).
 Xem đáp án
Xem đáp án
a) Ta có: \(\widehat A = 180^\circ - 60^\circ - 45^\circ = 75^\circ \)
Theo định lý sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
⇒ \[b = \frac{{a.\sin B}}{{\sin A}} = \frac{{a.\sin 60^\circ }}{{\sin 75^\circ }} = \frac{{a\sqrt 3 }}{{2\sin 75^\circ }}\]
Tương tự ta được \[c = \frac{{a\sqrt 2 }}{{2\sin 75^\circ }}\]
b) Kẻ AH vuông góc BC khi đó BH + HC = BC
\(HC + \frac{{b\sqrt 2 }}{2} + \frac{c}{2} = \frac{{a\sqrt 6 + a\sqrt 2 }}{{4\sin 75^\circ }}\)
\(a = \frac{{b\sqrt 2 }}{2} + \frac{c}{2} = \frac{{a\sqrt 6 + a\sqrt 2 }}{{4\sin 75^\circ }}\)
\(\sin 75^\circ = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
Mà sin275° + cos275° = 1
Suy ra: \(\cos 75^\circ = \frac{{\sqrt 6 - \sqrt 2 }}{4}\).
Câu 43:
Đồ thị hàm số y = x – 3 cắt trục hoành Ox tại điểm có tọa độ là?
 Xem đáp án
Xem đáp án
Đồ thị hàm số y = x − 3 cắt trục hoành Ox
⇒ y = 0
Thay y = 0 vào y = x – 3 ta có:
x – 3 = 0
⇔ x = 3
Vậy đồ thị hàm số y = x − 3 cắt trục hoành Ox tại điểm có tọa độ là (3;0).
Câu 44:
Cho tập A ≠ ∅ . Trong các mệnh đề sau, tìm mệnh đề sai?
 Xem đáp án
Xem đáp án
Đáp án đúng: D
Ta thấy: ∅ ⸦ A, A ⸦ A, ∅ ⸦ ∅ nên:
A ∪ ∅ = A
A ∪ A = A
∅ ∪ ∅ = ∅
Do đó đáp án A, B, C đều đúng.
Câu 45:
 Xem đáp án
Xem đáp án
A = sinxcosx
2A + 1 = 2sinxcosx + 1
2A + 1 = 2sinxcosx + sin2x + cos2x
2A + 1 = (sinx + cosx)2 = m2
A = \(\frac{{{m^2} - 1}}{2}\).
Câu 46:
Cho tam giác ABC, đường cao kẻ từ A ký hiệu là ha. Chứng minh:
ha = 2RsinBsinC.
 Xem đáp án
Xem đáp án
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R \Rightarrow \sin B = \frac{b}{{2R}},\sin C = \frac{c}{{2R}}\]
Khi đó: 2RsinBsinC = \[2R.\frac{b}{{2R}}.\frac{c}{{2R}} = \frac{{bc}}{{2R}}\]
Lại có: \(S = \frac{{abc}}{{4R}} = \frac{1}{2}a.{h_a} \Rightarrow \frac{{bc}}{{4R}} = \frac{1}{2}{h_a} \Leftrightarrow {h_a} = \frac{{bc}}{{2R}}\)
Vậy : ha = 2RsinBsinC.
Câu 47:
Chứng minh số \(\sqrt 2 \) là số vô tỉ.
 Xem đáp án
Xem đáp án
Giả sử \(\sqrt 2 \) không phải là số vô tỉ. Khi đó tồn tại các số nguyên a và b sao cho \(\sqrt 2 = \frac{a}{b}\) với b > 0. Hai số a và b không có ước chung nào khác 1 và –1.
Ta có: \({\left( {\sqrt 2 } \right)^2} = {\left( {\frac{a}{b}} \right)^2}\)(1)
Kết quả trên chứng tỏ a là số chẵn, nghĩa là ta có a = 2c với c là số nguyên.
Thay a = 2c vào (1) ta được: (2c)2 = 2b2 hay b2 = 2c2
Kết quả trên chứng tỏ b phải là số chẵn.
Hai số a và b đều là số chẵn, trái với giả thiết a và b không có ước chung nào khác 1 và –1.
Vậy \(\sqrt 2 \) là số vô tỉ.
Câu 48:
Một đội công nhân có 77 người nhận sửa xong một quãng đường trong 9 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người ? (mức làm của mỗi người như nhau)
 Xem đáp án
Xem đáp án
Nếu muốn sửa xong quãng đường trong 1 ngày thì cần số người là:
77 . 9 = 693 (người)
Muốn làm xong quảng đường đó trong 7 ngày thì số người là:
693 : 7 = 99 (người)
Cần thêm số người là:
99 – 77 = 22 (người)
Đáp số: 22 người.
Câu 49:
Giải phương trình sinx + sin2x + sin3x= cosx + cos2x + cos3x.
 Xem đáp án
Xem đáp án
sinx + sin2x + sin3x= cosx + cos2x+ cos3x
⇔ 2sin2xcosx + sin2x = 2cos2xcosx + cos2x
⇔ sin2x(2cosx + 1) = cos2x(2cosx + 1)
⇔ (2cosx + 1)(sin2x – cos2x) = 0
⇔ \(\left[ \begin{array}{l}\cos x = \frac{{ - 1}}{2}\\\sin \left( {2x - \frac{\pi }{4}} \right) = 0\end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = \pm \frac{{2\pi }}{3} + k2\pi \\2x - \frac{\pi }{4} = k\pi \end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = \pm \frac{{2\pi }}{3} + k2\pi \\x = \frac{\pi }{8} + k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Câu 50:
Tìm tất cả các giá trị của m để hàm số \(y = \frac{{mx + 16}}{{x + m}}\) đồng biến trên (0; +∞)?
 Xem đáp án
Xem đáp án
Điều kiện xác định: x ≠ –m
Ta có: \(y' = \frac{{{m^2} - 16}}{{{{\left( {x + m} \right)}^2}}}\)
Hàm số đồng biến trên (0;+∞) khi: \(\left\{ \begin{array}{l} - m \notin \left( {0; + \infty } \right)\\{m^2} - 16 > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - m \le 0\\\left[ \begin{array}{l}m > 4\\m < - 4\end{array} \right.\end{array} \right. \Leftrightarrow m > 4\)
Vậy m > 4.
Câu 51:
Cho hàm số y = x3 − (m + 1)x2 − (2m2 − 3m + 2)x + 2m(2m − 1). Tìm tất cả các giá trị thực của tham số m để hàm số đã cho đồng biến trên [2;+∞).
 Xem đáp án
Xem đáp án
Ta có y' = 3x2 − 2(m + 1)x − (2m2 − 3m + 2)
Xét phương trình y' = 0 có
Δ' = (m + 1)2 + 3(2m2 − 3m + 2) = 7(m2 – m + 1) > 0, ∀m ∈ ℝ.
Suy ra phương trình y' = 0 luôn có hai nghiệm x1 < x2 với mọi m .
Để hàm số đồng biến trên [2;+∞) ⇔ phương trình y' = 0 có hai nghiệm x1 < x2 ≤ 2
⇔ \(\left\{ \begin{array}{l}\left( {{x_1} - 2} \right) + \left( {{x_2} - 2} \right) < 0\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) \ge 0\end{array} \right.\)
⇔ \(\left\{ \begin{array}{l}{x_1} + {x_2} < 4\\{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4 \ge 0\end{array} \right.\)
⇔ \(\left\{ \begin{array}{l}\frac{{2\left( {m + 1} \right)}}{3} < 4\\\frac{{ - \left( {2{m^2} - 3m + 2} \right)}}{3} - 2.\frac{{2\left( {m + 1} \right)}}{3} + 4 \ge 0\end{array} \right.\)
⇔ \(\left\{ \begin{array}{l}m < 5\\ - 2 \le m \le \frac{3}{2}\end{array} \right. \Leftrightarrow - 2 \le m \le \frac{3}{2}\).
Câu 52:
1 người đi xe đạp trên đoạn đường MN. Trên nửa đầu của đoạn MN đi với tốc độ 20km/h. Trên nửa còn lại thì \(\frac{1}{2}\)thời gian đầu đi với tốc độ 10km/h; trên \(\frac{1}{2}\)thời gian còn lại đi với tốc độ 5 km/h. Tính tốc độ trung bình trên đoạn MN.
 Xem đáp án
Xem đáp án
Gọi quãng đường MN là s, thời gian đi hết quãng đường là t
Thời gian xe đi với vận tốc 20km/h là: \({t_1} = \frac{s}{{2.20}} = \frac{s}{{40}}\)
Thời gian còn lại: \({t_2} = t - {t_1} = t - \frac{s}{{40}}\)
Nửa quãng đường còn lại là:
\(\frac{{t - \frac{s}{{40}}}}{2}\left( {10 + 5} \right) = 7,5t - \frac{{3s}}{{16}} = \frac{s}{2}\)
⇔ 7,5t = 0,6875s
Suy ra: \(s = \frac{{120}}{{11}}t\)
Vận tốc trung bình là: \(\frac{{\frac{{120}}{{11}}t}}{t} = \frac{{120}}{{11}} \approx 10,91km/h\).
Câu 53:
Cho tam giác ABC vuông tại A. Đặt BC = a, AC = b, AB = c, kẻ đường cao AH của tam giác ABC. Tính tỉ số \(\frac{{BH}}{{CH}}\) theo a, b, c.
 Xem đáp án
Xem đáp án
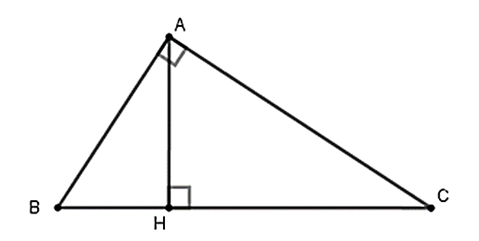
Áp dụng hệ thức lượng trong tam giác vuông ta dó:
AB2 = BH.BC hay c2 = BH.a
Suy ra: \(BH = \frac{{{c^2}}}{a}\)
AC2 = CH.BC suy ra: \(CH = \frac{{{b^2}}}{a}\)
\(\frac{{BH}}{{CH}} = \frac{{{c^2}}}{a}:\frac{{{b^2}}}{a} = \frac{{{c^2}}}{{{b^2}}}\).
Câu 55:
Giải phương trình: \(\frac{{21}}{{{x^2} - 4x + 10}} = {x^2} - 4x + 6\).
 Xem đáp án
Xem đáp án
Điều kiện xác định: x ∈ ℝ
\(\frac{{21}}{{{x^2} - 4x + 10}} = {x^2} - 4x + 6\)
⇔ (x2 – 4x + 6)(x2 – 4x + 10) = 21
⇔ (x2 – 4x + 6)(x2 – 4x + 10) – 21 = 0 (*)
Đặt x2 – 4x + 8 = t
Ta thấy t > 0 vì x2 – 4x + 8 = (x – 2)2 + 2 > 0 với mọi x
(*) trở thành: (t – 2)(t + 2) – 21 = 0
⇔ t2 – 4 – 21 = 0
⇔ t2 – 25 = 0
⇔ \(\left[ \begin{array}{l}t = 5\\t = - 5\end{array} \right.\)
Chọn t = 5 vì t > 0
Suy ra: x2 – 4x + 8 = 5
⇔ x2 – 4x + 3 = 0
⇔ (x – 1)(x – 3) = 0
⇔ \(\left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Vậy phương trình có nghiệm x = 1 hoặc x = 3.
Câu 56:
Tìm x, y, z thỏa mãn 2x2 + 2y2 + z2 + 25 – 6y – 2xy – 8x + 2z(y – x) = 0.
 Xem đáp án
Xem đáp án
2x2 + 2y2 + z2 + 25 – 6y – 2xy – 8x + 2z(y – x) = 0
⇔ (y – x)2 + 2z(y – x) + z2 + x2 – 8x + 16 + y2 – 6x + 9 = 0
⇔ (y – x + z)2 + (x – 4)2 + (y – 3)2 = 0
Ta thấy: (y – x + z)2 + (x – 4)2 + (y – 3)2 luôn ≥ 0 với mọi x, y, z
Nên phương trình bằng 0 khi:
\(\left\{ \begin{array}{l}y - x + z = 0\\x - 4 = 0\\y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\\z = x - y = 4 - 3 = 1\end{array} \right.\)
Vậy (x; y; z) = (4; 3; 1).
Câu 57:
Cho hình thang vuông ABCD có AB = BC = a, AD = 2a. Chứng minh AC vuông góc DC.
 Xem đáp án
Xem đáp án
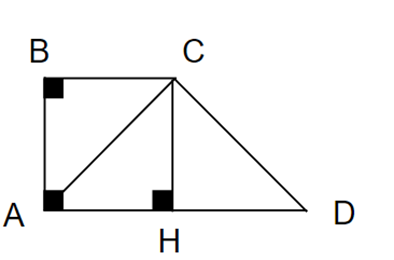
Vẽ CH vuông góc AD
Xét tứ giác ABCH có: \(\widehat A = \widehat B = \widehat H = 90^\circ \) nên ABCH là hình chữ nhật
Suy ra: AB = CH = a; BC = AH = a
Xét tam giác CHA có:
CH = HA = a
\(\widehat {CHA} = 90^\circ \)
Nên tam giác CHA vuông cân tại H
Suy ra: \(\widehat {HCA} = \widehat {AHC} = 45^\circ \)
Lại có: AD = a nên HD = AD – AH = 2a – a = a
Suy ra: CH = HD nên tam giác CHD vuông cân tại H
⇒ \(\widehat {HCD} = \widehat {CDH} = 45^\circ \)
\(\widehat {ACD} = \widehat {ACH} + \widehat {HCD} = 45^\circ + 45^\circ = 90^\circ \)
Hay AC vuông góc CD.
Câu 58:
Cho tam giác ABC có AB = 1, \(\widehat A = 105^\circ ,\widehat B = 60^\circ \). Trên cạnh BC lấy điểm E sao cho BE = 1. Vẽ ED song song với AB. Chứng minh: \(\frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}} = \frac{4}{3}\).
 Xem đáp án
Xem đáp án
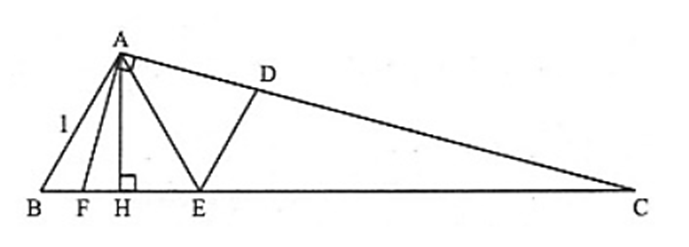
Vẽ AH ⊥ BC (H ∈ BC) ; AF ⊥ AC (F ∈ AC) (xem hình)
Từ các dữ kiện đề bài AB = BE = 1, \(\widehat {ABE} = 60^\circ \)⇒ ΔABE đều
AH ⊥ BE ⇒ AH là đường cao cũng là đường trung tuyến nên
BH = BE : 2 = 0,5
Áp dụng định lý Pi–ta–go vào ΔAHB ⊥ H:
AH2 = AB2 – BH2 = AB2 – \({\left( {\frac{{BE}}{2}} \right)^2} = 1 - \frac{1}{4} = \frac{3}{4}\left( 1 \right)\)
\(\widehat {ACB} = 180^\circ - \widehat {BAC} - \widehat {ABC} = 180^\circ - 105^\circ - 60^\circ = 15^\circ \)
\(\widehat {BAF} = \widehat {BAC} - \widehat {FAC} = 105^\circ - 90^\circ = 15^\circ \)
Suy ra: \(\widehat {ACB} = \widehat {BAF}\)
Xét tam giác ABC và tam giác FBA có:
\(\widehat {ACB} = \widehat {BAF}\)
Chung \(\widehat B\)
⇒ ∆ABC ∽ ∆FBA (g.g)
⇒ \(\frac{{AF}}{{AC}} = \frac{{AB}}{{BC}} = \frac{{BE}}{{BC}} = \frac{{AD}}{{AC}}\)(do ED // AB)
Nên AF = AD (2)
Tam giác AFC vuông tại A, đường cao AH nên có hệ thức lượng:
\(\frac{1}{{A{C^2}}} + \frac{1}{{A{F^2}}} = \frac{1}{{A{H^2}}} = \frac{4}{3}\)
Mà AF = AD nên \(\frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}} = \frac{4}{3}\).
Câu 59:
Cho tam giác vuông ABC có \(\widehat A = 90^\circ \). Kết quả nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng: B
Ta có: \(\widehat A = 90^\circ \) nên sin2A = sin290° = 1
Mà ta có định lý sin2α + cos2α = 1
Nên: cos2C + sin2C = cos2B + sin2B = sin2A = 1.
Câu 60:
Cho định lí: "Nếu m,n là hai số nguyên dương và mỗi số đều chia hết cho 3 thì m2 + n2 cũng chia hết cho 3". Hãy phát biểu và chứng định lí đảo của định lí trên (nếu có).
 Xem đáp án
Xem đáp án
Định lí đảo : “Nếu m, n là hai nguyên dương và m² + n² chia hết cho 3 thì cả m và n đều chia hết cho 3”.
Nếu một số không chia hết cho 3 và số kia chia hết cho 3 thì rõ ràng tổng bình phương hai số đó không chia hết cho 3. Giả sử m và n đều không chia hết cho 3. Nếu m = 3k + 1 hoặc 3k + 2 ta đều có m² chia 3 dư 1 thành thử m² + n² chia 3 dư 2.
Vậy nếu m² + n² chia hết cho 3 thì chỉ có thể xảy ra khả năng cả m và n đều chia hết cho 3.
Vậy: Điều kiện cần và đủ để m² + n² chia hết cho 3 (m, n ∈ ℕ) là cả m và n đều chia hết cho 3.
Câu 61:
Giải phương trình: \(\cos \left( {3x + \frac{\pi }{4}} \right) = 0\).
 Xem đáp án
Xem đáp án
\(\cos \left( {3x + \frac{\pi }{4}} \right) = 0\)
⇔ \(3x + \frac{\pi }{4} = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\)
⇔ \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\).
Câu 62:
Giải phương trình: cos3x – sin3x = 1.
 Xem đáp án
Xem đáp án
cos3x – sin3x = 1
⇔ \(\frac{{\sqrt 2 }}{2}\cos 3x - \frac{{\sqrt 2 }}{2}\sin 3x = \frac{{\sqrt 2 }}{2}\)
⇔ \(\cos \left( {3x + \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right)\)
⇔ \(\left[ \begin{array}{l}3x + \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \\3x + \frac{\pi }{4} = - \frac{\pi }{4} + k2\pi \end{array} \right.\)
\[ \Leftrightarrow \left[ \begin{array}{l}x = k\frac{{2\pi }}{3}\\x = - \frac{\pi }{3} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\].
Câu 63:
Các góc nhìn đến đinh núi có chiều cao là TN so với mực nước biển được đo từ hai đèn tín hiệu tại A và B trên mặt biển.
Biết \(\widehat {TAB} = 29,7^\circ ,\widehat {TBN} = 41,2^\circ \) AB = 1500m.
Hỏi chiều cao TN của ngọn núi khoảng bao nhiêu mét? (làm tròn kết quả đến một chữ số thập phân).
 Xem đáp án
Xem đáp án
\(\tan 29,7^\circ = \frac{{TN}}{{AN}} \Rightarrow {\rm A}{\rm N} = \frac{{TN}}{{\tan 29,7^\circ }}\)
\(\tan 41,2^\circ = \frac{{TN}}{{BN}} \Rightarrow B{\rm N} = \frac{{TN}}{{\tan 41,2^\circ }}\)
AN – BN = \(\frac{{TN}}{{\tan 29,7^\circ }} - \frac{{TN}}{{\tan 41,2^\circ }} = TN\left( {\frac{1}{{\tan 29,7^\circ }} - \frac{1}{{\tan 41,2^\circ }}} \right)\)
AB = TN.0,61
⇔ 1500 = TN.0,61
⇔ TN = 2455,4 (m).
Câu 64:
Có 5 người thợ dệt trong 8 giờ được 240 sản phẩm. Hỏi muốn làm được 192 sản phẩm như thế thì 4 người phải làm trong bao lâu? (Mức lao động của mỗi người là như nhau)
 Xem đáp án
Xem đáp án
5 người thợ làm trong 1 giờ được số sản phẩm là:
240 : 8 = 30 (sản phẩm)
1 người thợ làm trong 1 giờ được số sản phẩm là:
30 : 5 = 6 (sản phẩm)
4 người thợ làm trong 1 giờ được số sản phẩm là:
6 . 4 = 24 (sản phẩm)
Để làm được 192 sản phẩm như thế, 4 người cần làm số giờ là:
192 : 24 = 8 (giờ).
Câu 65:
Tìm điều kiện xác định: \[\sqrt {2x - 3} \].
 Xem đáp án
Xem đáp án
Điều kiện: 2x – 3 ≥ 0
Hay x ≥ \(\frac{3}{2}\).
Câu 66:
Hàm số y = f(x2 + 2x) nghịch biến trên khoảng nào?
|
x |
–∞ |
–2 |
1 |
3 +∞ |
|
f'(x) |
– |
0 + |
0 – |
0 – |
 Xem đáp án
Xem đáp án
y = f(x2 + 2x)
y' = (2x + 2)f'(x2 + 2x)
Xét y' = 0 ta có: (2x + 2)f'(x2 + 2x) = 0
⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)
Ta có bảng biến thiên:
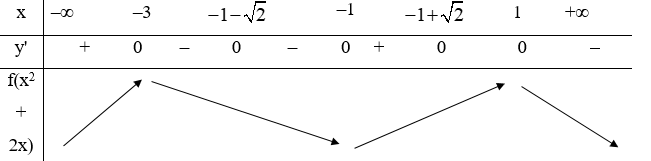
Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)
Câu 67:
Một người đi bộ đều quãng đường đầu dài 3km với vận tốc 2m/s. Ở quãng đường tiếp theo dài 1,95km người đó đi hết 0,5h. Tính vận tốc trung bình của người đó trên cả hai quãng đường.
 Xem đáp án
Xem đáp án
Thời gian người đi bộ đi hết quãng đường thứ nhất là:
\({t_1} = \frac{{{S_1}}}{{{v_1}}} = \frac{{3000}}{2} = 1500\left( s \right)\)
Vận tốc trung bình của người đi bộ trên cả hai đoạn đường là:
\({v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}} = \frac{{3000 + 1950}}{{1500 + 1800}} = 1,5\left( {m/s} \right)\).
Câu 68:
Tìm giá trị nhỏ nhất, lớn nhất của hàm số y = 4cos22x – 4cosx + 2.
 Xem đáp án
Xem đáp án
y = 4cos22x – 4cosx + 2
= (2cosx – 1)2 + 1
Do –1 ≤ cosx ≤ 1 với mọi x nên – 3 ≤ 2cosx – 1 ≤ 1
⇒ 0 ≤ (2cosx – 1)2 ≤ 9
1 ≤ (2cosx – 1)2 + 1 ≤ 10
Hay 1 ≤ y ≤ 10.
Vậy giá trị nhỏ nhất của y là 1 khi 2cosx – 1 = 0 hay cosx = \(\frac{1}{2} = \cos \left( {\frac{\pi }{3}} \right) \Leftrightarrow x = \pm \frac{\pi }{3} + k2\pi \)
Giá trị lớn nhất của y là 10 khi 2cosx – 1 = – 3 hay cosx = –1 tức \(x = \pi + k2\pi \) (k ∈ ℤ).
Câu 69:
Tìm giá trị nhỏ nhất lớn nhất của \(y = 2\sin \left( {x - \frac{\pi }{2}} \right) + 3\).
 Xem đáp án
Xem đáp án
Ta có: –1 ≤ \(\sin \left( {x - \frac{\pi }{2}} \right)\)≤ 1
Suy ra: –2 ≤ \(2\sin \left( {x - \frac{\pi }{2}} \right)\)≤ 2
1 ≤ \(2\sin \left( {x - \frac{\pi }{2}} \right) + 3\) ≤ 5
Hay 1 ≤ y ≤ 5.
Vậy giá trị nhỏ nhất y = 1 khi \(\sin \left( {x - \frac{\pi }{2}} \right) = - 1\)
⇔ \(x - \frac{\pi }{2} = - \frac{\pi }{2} + k2\pi \) hay \(x = k2\pi \left( {k \in \mathbb{Z}} \right)\)
Giá trị lớn nhất y = 5 khi \(\sin \left( {x - \frac{\pi }{2}} \right) = 1\)
⇔ \(x - \frac{\pi }{2} = \frac{\pi }{2} + k2\pi \) hay \(x = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 70:
Tìm GTLN và GTNN của y = (sinx – 2cosx)(2sinx + cosx) – 1.
 Xem đáp án
Xem đáp án
y = (sinx – 2cosx)(2sinx + cosx) – 1
= 2sin2x + sinx.cosx – 4sinx.cosx – 2cos2x – 1
= –2(cos2x – sin2x) – 3sinx.cosx – 1
= –2cos2x – \(\frac{3}{2}\sin 2x - 1\)
Suy ra: y + 1 = –2cos2x – \(\frac{3}{2}\sin 2x\)
Điều kiện xác định có nghiệm: (y + 1)2 ≤ (–2)2 + \({\left( {\frac{{ - 3}}{2}} \right)^2}\)
(y + 1)2 ≤ 4 + \(\frac{9}{4} = \frac{{25}}{4}\)
Suy ra: \(\frac{{ - 5}}{2} \le y + 1 \le \frac{5}{2}\)
⇒ \(\frac{{ - 7}}{2} \le y \le \frac{3}{2}\)
Vậy giá trị nhỏ nhất của y là \(\frac{{ - 7}}{2};\)giá trị lớn nhất là \(\frac{3}{2}.\) \[\]
Câu 71:
Tìm giá trị nhỏ nhất, lớn nhất của hàm số y = sinx + \(\sin \left( {x + \frac{{2\pi }}{3}} \right)\).
 Xem đáp án
Xem đáp án
y = sinx + \(\sin \left( {x + \frac{{2\pi }}{3}} \right)\)
= sinx – \(\frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \sin \left( {x + \frac{\pi }{3}} \right)\)
Ta có: –1 ≤ sinx ≤ 1 với mọi x
Nên –1 ≤ \(\sin \left( {x + \frac{\pi }{3}} \right)\) ≤ 1
Vậy giá trị lớn nhất của y = 1 khi \(\sin \left( {x + \frac{\pi }{3}} \right) = 1 \Leftrightarrow x = \frac{\pi }{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
Giá trị nhỏ nhất của y = – 1 khi \(\sin \left( {x + \frac{\pi }{3}} \right) = - 1 \Leftrightarrow x = - \frac{{5\pi }}{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 72:
Tìm tập xác định của hàm số y = tanx – cot2x.
 Xem đáp án
Xem đáp án
Điều kiện xác định: \(\left\{ \begin{array}{l}\sin 2x \ne 0\\\cos x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x \ne k\pi \\x \ne \frac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{{k\pi }}{2}\\x \ne \frac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow x \ne \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\)
Vậy tập xác định: \[D = R\backslash \left\{ {\frac{{k\pi }}{2}} \right\},k \in \mathbb{Z}\].
Câu 73:
Đồ thị hàm số y = x3 − 3x2 − 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?
 Xem đáp án
Xem đáp án
Đáp án đúng: D
Xét hàm số: y = f(x) = x3 − 3x2 − 9x + 1
f’(x) = 3x2 – 6x – 9
Ta có: f(x) = \(\left( {\frac{1}{3}x - \frac{1}{3}} \right)f'\left( x \right) - 8x - 2\)
Đồ thị hàm số f(x) có hai điểm cực trị A và B nên f’(xA) = f’(xB) = 0
Suy ra: \(\left\{ \begin{array}{l}{y_A} = f\left( {{x_A}} \right) = - 8{x_A} - 2\\{y_B} = f\left( {{x_B}} \right) = - 8{x_B} - 2\end{array} \right.\)
Do đó phương trình đường thẳng AB là y = –8x – 2
Khi đó ta có N(1;–10) thuộc đường thẳng AB.
Câu 74:
Giải phương trình: sin4x + \({\cos ^4}\left( {x + \frac{\pi }{4}} \right) = \frac{1}{4}\).
 Xem đáp án
Xem đáp án
sin4x + \({\cos ^4}\left( {x + \frac{\pi }{4}} \right) = \frac{1}{4}\)
⇔ sin4x + \({\left( {\cos x.\frac{1}{{\sqrt 2 }} - \sin x.\frac{1}{{\sqrt 2 }}} \right)^4} = \frac{1}{4}\)
⇔ sin4x + \(\frac{1}{4}{\left( {\cos x - \sin x} \right)^4} = \frac{1}{4}\)
⇔ sin4x + \(\frac{1}{4}{\left[ {{{\left( {\cos x - \sin x} \right)}^2}} \right]^2} = \frac{1}{4}\)
⇔ sin4x + \(\frac{1}{4}{\left( {{{\cos }^2}x - 2\sin x\cos x + {{\sin }^2}x} \right)^2} = \frac{1}{4}\)
⇔ sin4x + \(\frac{1}{4}{\left( {1 - 2\sin x\cos x} \right)^2} = \frac{1}{4}\)
⇔ sin4x + sin2xcos2x – sinxcosx = 0
⇔ sinx(sin3x + sinxcos2x – cosx) = 0
⇔ \(\left[ \begin{array}{l}\sin x = 0\left( 1 \right)\\{\sin ^3}x + \sin x{\cos ^2}x - \cos x = 0\left( 2 \right)\end{array} \right.\)
(1): x = kπ
(2): sinx(sin2 + cos2x) – cosx = 0
⇔ sinx – cosx = 0
⇔ \(\sin \left( {x - \frac{\pi }{4}} \right) = 0\)
⇔ \(x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình có nghiệm: \(x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 75:
Giải phương trình: 4(sin4x + cos4x) + \(\sqrt 3 \sin 4x = 2\).
 Xem đáp án
Xem đáp án
4(sin4x + cos4x) + \(\sqrt 3 \sin 4x = 2\)
⇔ 4[(sin2x + cos2x) – 2.sin2x.cos2x + \(\sqrt 3 \sin 4x = 2\)
⇔ \(4\left( {1 - \frac{1}{2}{{\sin }^2}2x} \right) + \sqrt 3 \sin 4x = 2\)
⇔ \(4\left[ {1 - \frac{1}{2}.\left( {\frac{1}{2} - \frac{1}{2}\cos 4x} \right)} \right] + \sqrt 3 \sin 4x = 2\)
⇔ \(4.\frac{3}{4} + 4.\frac{1}{4}.\cos 4x + \sqrt 3 \sin 4x = 2\)
⇔ cos4x + \(\sqrt 3 \sin 4x = - 1\)
⇔ \(\frac{1}{2}\cos 4x + \frac{{\sqrt 3 }}{2}\sin 4x = \frac{{ - 1}}{2}\)
⇔ \(\sin \left( {\frac{\pi }{6}} \right)\cos 4x + \cos \left( {\frac{\pi }{6}} \right)\sin 4x = \frac{{ - 1}}{2}\)
⇔ \(\sin \left( {4x + \frac{\pi }{6}} \right) = \frac{{ - 1}}{2}\)
⇔ \(\left[ \begin{array}{l}4x + \frac{\pi }{6} = \frac{{ - \pi }}{6} + k2\pi \\4x + \frac{\pi }{6} = \pi + \frac{\pi }{6} + k2\pi \end{array} \right.\)
⇔ \(\left[ \begin{array}{l}x = \frac{{ - \pi }}{{12}} + k\frac{\pi }{2}\\x = \frac{\pi }{4} + k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Câu 76:
Tìm x để P2 > P biết P = \[\frac{{\sqrt x + 1}}{{\sqrt x - 1}}\].
 Xem đáp án
Xem đáp án
Vì P2 > P nên P2 – P > 0 hay P(P – 1) > 0
⇔ \[\left[ \begin{array}{l}\left\{ \begin{array}{l}P > 0\\P > 1\end{array} \right.\\\left\{ \begin{array}{l}P < 0\\P < 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}P > 1\\P < 0\end{array} \right.\]
Với P >1 thì \[\frac{{\sqrt x + 1}}{{\sqrt x - 1}} > 1\]
⇔ \[\frac{{\sqrt x + 1}}{{\sqrt x - 1}} - 1 > 0\]
⇔ \[\frac{{\sqrt x + 1 - \sqrt x + 1}}{{\sqrt x - 1}} > 0\]
⇔ \[\frac{2}{{\sqrt x - 1}} > 0\]
Mà 2 > 0 nên \[\sqrt x - 1 > 0 \Rightarrow x > 1\]
Với P < 0 thì \[\frac{{\sqrt x + 1}}{{\sqrt x - 1}} < 0\]
Mà \[\sqrt x + 1 > 0 \Rightarrow \sqrt x - 1 < 0 \Rightarrow x < 1\]
Kết hợp điều kiện xác định x ≥ 0 nên 0 ≤ x < 1
Vậy để P2 > P khi \(\left[ \begin{array}{l}x > 1\\0 \le x < 1\end{array} \right.\).
Câu 77:
Giải phương trình sau: 2cosx.cos2x = 1 + cos2x + cos3x.
 Xem đáp án
Xem đáp án
2cosx.cos2x = 1 + cos2x + cos3x
⇔ 2cosx.cos2x = 2cos2x + 4cos3x – 3cosx
⇔ cosx[2(2cos2x – 1) – 2cosx – 4cos2x + 3] = 0
⇔ cosx(–2cosx + 1) = 0
⇔ \(\left[ \begin{array}{l}\cos x = 0\\ - 2\cos x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k\pi \\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Câu 78:
Cho ∆ABC có \(\widehat A\) = 30°, AB = 4cm; S = 16 cm2. Tính AC?
 Xem đáp án
Xem đáp án
Ta có: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC}\)
Hay: \(6 = \frac{1}{2}.4.AC.\sin 30^\circ \)
Suy ra: AC = 6 (cm).
Câu 79:
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \sqrt {5 - m\sin x - \left( {m + 1} \right)\cos x} \) xác định trên ℝ?
 Xem đáp án
Xem đáp án
Hàm số xác định trên ℝ.
⇔ 5 – msinx − (m + 1)cosx ≥ 0 ∀x ∈ ℝ
⇔ m.sinx ‒ (m + 1)cosx ≤ 5 ∀ ∈ ℝ
⇔ m2 + (m + 1)2 ≤ 25
⇔ m2 + m ‒ 12 ≤ 0
⇔ m ∈ [−4;3]
Vậy có 8 giá trị nguyên của m thỏa mãn.
Câu 80:
Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp {1; 4; 7; 10; 13; 16; 19}.
 Xem đáp án
Xem đáp án
Có 13 số nguyên: {12; 15; 18; 21; 24; 27; 30; 33; 36; 39; 42; 45; 48}.
Câu 81:
Hiện nay em 4 tuổi, anh 10 tuổi. Hỏi mấy năm nữa tuổi anh gấp đôi tuổi em?
 Xem đáp án
Xem đáp án
Anh hơn em số tuổi là:
10 – 4 = 6 (tuổi)
Vì mỗi năm anh tăng 1 tuổi thì em cũng tăng 1 tuổi, nên hiệu số tuổi của hai anh em luôn không đổi. Vậy khi tuổi anh gấp đôi số tuổi của em thì anh vẫn hơn em 6 tuổi.
Số tuổi của em khi tuổi anh bằng hai lần tuổi em là:
6 : (2 – 1) = 6 (tuổi)
Sau số năm nữa tuổi anh gấp 2 lần tuổi em là:
6 – 4 = 2 (năm)
Đáp số: 2 năm.
Câu 82:
 Xem đáp án
Xem đáp án
sin3x + cos3x = 1 – \(\frac{1}{2}\sin 2x\)
⇔ (sinx + cosx)(sin2x – sinxcosx + cos2x) = 1 – \(\frac{1}{2}\sin 2x\)
⇔ (sinx + cosx)(1 – sinxcosx) = 1 – \(\frac{1}{2}\sin 2x\)
⇔ (sinx + cosx)\(\left( {1 - \frac{1}{2}\sin 2x} \right) = 1 - \frac{1}{2}\sin 2x\)
⇔ \(\left( {1 - \frac{1}{2}\sin 2x} \right)\left( {\sin x + \cos x - 1} \right) = 0\)
⇔ \(\left[ \begin{array}{l}\sin 2x = 2 > 1\left( L \right)\\\sin x + \cos x - 1 = 0\end{array} \right.\)
⇔ sinx + cosx = 1
⇔ \(\cos \left( {x - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2} = \cos \left( {\frac{\pi }{4}} \right)\)
⇔ \(x - \frac{\pi }{4} = \pm \frac{\pi }{4} + k2\pi \)
⇔ \(\left[ \begin{array}{l}x = k2\pi \\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Câu 83:
Trong các tập hợp sau tập nào là con của tập nào: A = “Tập các tam giác cân”, B = “Tập các tam giác đều”, C = “Tập các tam giác vuông”, D = “Tập các tam giác vuông cân”.
 Xem đáp án
Xem đáp án
Quan hệ tập con:
B ⊂ A (Tam giác đều là tam giác cân có 1 góc 60°)
D ⊂ A(Tam giác vuông cân là tam giác cân có góc ở đỉnh bằng 90°)
D ⊂ C (Tam giác vuông cân là tam giác vuông có 2 góc nhọn bằng 45°).
Câu 84:
Tìm GTLN, GTNN của hàm số y = sin2x – cos2x + 2sinxcosx + 5.
 Xem đáp án
Xem đáp án
y = sin2x – cos2x + 2sinxcosx + 5
= sin2x – cos2x + 5
= \(\sqrt 2 \sin \left( {2x - \frac{\pi }{4}} \right) + 5\)
Ta có: –1 ≤ \(\sin \left( {2x - \frac{\pi }{4}} \right)\) ≤ 1
⇒ \( - \sqrt 2 \le \sqrt 2 \sin \left( {2x - \frac{\pi }{4}} \right) \le \sqrt 2 \)
⇒ \(5 - \sqrt 2 \le \sqrt 2 \sin \left( {2x - \frac{\pi }{4}} \right) + 5 \le 5 + \sqrt 2 \)
Hay \(5 - \sqrt 2 \le y \le 5 + \sqrt 2 \)
Vậy max y = \(5 + \sqrt 2 \) khi \(2x - \frac{\pi }{4} = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{{3\pi }}{8} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Min y = \(5 - \sqrt 2 \)khi \(2x - \frac{\pi }{4} = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = - \frac{\pi }{8} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 85:
Tìm GTLN, GTNN của hàm số y = –sin2x – cosx + 2.
 Xem đáp án
Xem đáp án
y = –sin2x – cosx + 2
= 1 – sin2x – cosx + 1
= cos2x – cosx + 1
= \({\left( {\cos x - \frac{1}{2}} \right)^2} + \frac{3}{4}\)
Vì –1 ≤ cosx ≤ 1
Nên: \(\frac{{ - 3}}{2} \le \cos x - \frac{1}{2} \le \frac{1}{2}\)
Suy ra: \(\frac{9}{4} \ge {\left( {\cos x - \frac{1}{2}} \right)^2} \ge \frac{1}{4}\)
⇔ \(3 \ge {\left( {\cos x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge 1\)
Vậy max y = 3 khi cosx = 1 ⇔ x = k2π (k ∈ ℤ).
Min y = 1 khi cosx = –1 ⇔ x = π + k2π (k ∈ ℤ).
Câu 86:
Thực hiện phép chia: [3(x – y)5 – 2(x – y)4 + 3(x – y)2] : 5(x – y)2.
 Xem đáp án
Xem đáp án
[3(x – y)5 – 2(x – y)4 + 3(x – y)2] : 5(x – y)2
= 3(x – y)5 : 5(x – y)2 – 2(x – y)4 : 5(x – y)2 + 3(x – y)2 : 5(x – y)2
= \(\frac{3}{5}{\left( {x - y} \right)^3} - \frac{2}{5}{\left( {x - y} \right)^2} + \frac{3}{5}\).
Câu 87:
Có một tấm vải dài 35m. Người ta đem cắt thành các mảnh vải nhỏ, mỗi mảnh vải dài 1,25m. Hỏi người ta cắt được bao nhiêu mảnh vải nhỏ?
 Xem đáp án
Xem đáp án
Người ta cắt được số mảnh vải nhỏ là:
35 : 1,25 = 28 (mảnh vải)
Đáp số: 28 mảnh vải.
Câu 88:
Cho tam giác ABC vuông cân tại A, đường cao AH. Từ điểm M bất kì trên cạnh BC (M không trùng với B và C) kẻ các đường thẳng song song với AC và AB ở D và cắt AC ở E. Chứng minh \[\widehat {DHE} = 90^\circ \].
 Xem đáp án
Xem đáp án
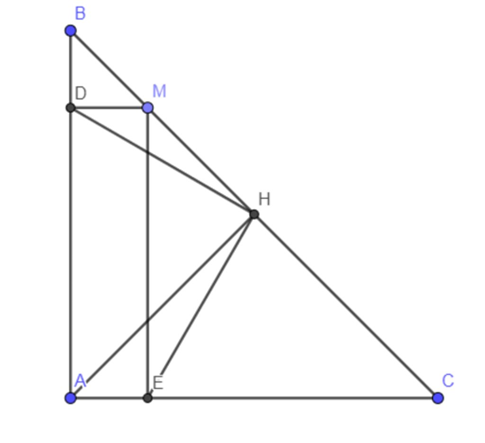
Do ΔABC vuông cân tại A có đường cao AH
⇒ AH = BH = \(\frac{1}{2}BC\)
Ta có
\[\widehat {BMD} = \widehat C\] (2 góc đồng vị)
\[\widehat B = \widehat C\](gt)
⇒ \[\widehat {BMD} = \widehat B\]
Mà MD // AC (gt)
AC ⊥ AB (gt)
⇒ MD ⊥ AB
⇒ \[\widehat {BDM} = 90^\circ \]
Do đó ΔBDM vuông cân tại D
⇒ BD = DM
Lại có tứ giác ADME là hình chữ nhật ( do \[\widehat {BAC} = \widehat {ADM} = \widehat {AEM} = 90^\circ \])
⇒ BD = DM = AE
Mặt khác ta có
\[\widehat {HAC} + \widehat C = 90^\circ \] (ΔACH vuông tại H)
\[\widehat B + \widehat C = 90^\circ \]
⇒ \(\widehat {HAE} = \widehat B\)
Xét ΔHAE và ΔHBD có
HA = HB (cmt)
\(\widehat {HAE} = \widehat B\)(cmt)
AE = BD (cmt)
⇒ ΔHAE = ΔHBD (c.g.c)
⇒ \[\widehat {AHE} = \widehat {BHD}\]
Mà \[\widehat {BHD} + \widehat {AHD} = \widehat {BHA} = 90^\circ \]
⇒ \[\widehat {DHE} = 90^\circ \]
Câu 89:
So sánh M và \(\sqrt M \) biết M = \(\frac{{2 - 5\sqrt a }}{{\sqrt a + 3}}\) với a > 0.
 Xem đáp án
Xem đáp án
\(\frac{{2 - 5\sqrt a }}{{\sqrt a + 3}} = \frac{{ - 5\left( {\sqrt a + 3} \right) + 15 + 2}}{{\sqrt a + 3}} = \frac{{ - 5\left( {\sqrt a + 3} \right) + 17}}{{\sqrt a + 3}} = - 5 + \frac{{17}}{{\sqrt a + 3}}\)
Vì \(\sqrt a \ge 0 \Rightarrow \sqrt a + 3 \ge 3 \Rightarrow \frac{{17}}{{\sqrt a + 3}} \le \frac{{17}}{3} \Rightarrow - 5 + \frac{{17}}{{\sqrt a + 3}} \le - 5 + \frac{{17}}{3} = \frac{2}{3}\)
Hay \(M < \frac{2}{3}\)
Suy ra: \(\sqrt M < M\).
Câu 91:
Cho a + b = 5; ab = 2. Tính a2 + b2.
 Xem đáp án
Xem đáp án
Ta có: (a + b)2 = 52 = 25
a2 + b2 + 2ab = 25
a2 + b2 = 25 – 2ab
a2 + b2 = 25 – 2.2
a2 + b2 = 21.
Vậy a2 + b2 = 21.
Câu 92:
Bạn Thanh giải một đề thi toán trắc nghiệm với 30 câu hỏi, cứ mỗi câu đúng bạn được cộng 5 điểm, và mỗi câu sai bị trừ (0hoặc không trả lời) bị trừ hai điểm, sau khi giải xong bạn được số điểm là 101 điểm. Hỏi bạn Thanh đã trả lời đúng bao nhiêu câu và sai bao nhiêu câu?
 Xem đáp án
Xem đáp án
Gọi số câu trả lời bạn Thanh trả lời đúng là: a (a ∈ ℕ*; a ≤ 30)
Số câu trả lời sai (hoặc không trả lời) là: 30 − a (câu)
Mỗi câu đúng được cộng 5 điểm và mỗi câu sai bị trừ 2 điểm nên tổng số điểm của Thanh là:
5.a − 2.(30 − a) = 101
⇔ 5a – 60 + 2a = 101
⇔ 7a = 161
⇔ a = 23
Vậy Thanh trả lời đúng 23 câu và trả lời sai 7 câu.
Câu 93:
Cho A(0; 2), B(6; 4), C(1; –1). Tìm tọa độ của các điểm M, N, P sao cho:
a) Tam giác ABC nhận M, N, P là trung điểm của các cạnh.
b) Tam giác MNP nhận các điểm A, B, C làm trung điểm của các cạnh.
 Xem đáp án
Xem đáp án
a) M, N, P là trung điểm AB, AC, BC
Nên: M(3;3), \(N\left( {\frac{1}{2};\frac{1}{2}} \right),P\left( {\frac{7}{2};\frac{3}{2}} \right)\)
b) A,B,C là trung điểm các cạnh MN, NP,MP
Giả sử M(xM;yM); N(xN;yN); P(xP;yP)
Ta có: xM + xN = 2.xA = 0
xN + xP = 2.xB = 12
xM + xP = 2.xC = 2
Suy ra: xM = –5; xN = 5; xP = 7.
Lại có:
yM + yN = 2.yA = 4
yM + yP = 2.yC = –2
yN + yP = 2.yB = 8
Suy ra: yM = –3; yN = 7; yP = 1.
Vậy M(–5; –3), N(5; 7), P(7; 1).
Câu 94:
Cho cấp số nhân (un) có số hạng đầu u1 = 6 và công bội q = 2. Tìm số hạng thứ tư của cấp số nhân đó.
 Xem đáp án
Xem đáp án
u4 = u1.q3 = 6.23 = 48.
Câu 95:
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.
a) Chứng minh E và F đối xứng với nhau qua AB.
b) Chứng minh tứ giác MEBF là hình thoi.
c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
 Xem đáp án
Xem đáp án
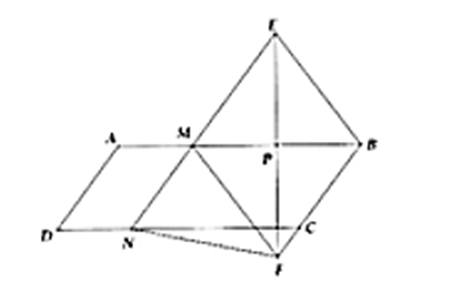
a) Do AM = DN và AM // DN (do AB // CD)
⇒ MADN là hình bình hành
⇒ \(\widehat D = \widehat {AMN} = \widehat {EMB} = \widehat {MBC}\)
Xét ∆MPE và ∆BPE có:
Chung PE
\(\widehat {MPE} = \widehat {BPE}\)
MP = BP (EP là trung trực MB)
Ta có ∆MPE = ∆BPE nên EP = FP.
Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB ∩ EF = P;
Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
⇒ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì \(\widehat {CNE} = \widehat {BEN}\)
Mà \(\widehat {CNE} = \widehat D = \widehat {EMB} = \widehat {MBC}\)
nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì \(\widehat {ABC} = 60^\circ \).
Câu 96:
Cho tam giác ABC có điểm O thỏa mãn \[\left| {\overrightarrow {OA} + \overrightarrow {OB} - 2\overrightarrow {OC} } \right| = \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|\]. Hỏi tam giác ABC là tam giác gì?
 Xem đáp án
Xem đáp án
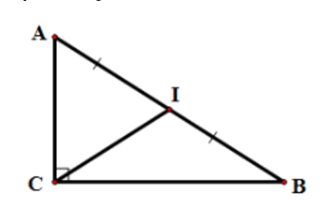
Gọi I là trung điểm AB
Suy ra: \[\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {CI} \]
Ta có: \[\left| {\overrightarrow {OA} + \overrightarrow {OB} - 2\overrightarrow {OC} } \right| = \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|\]
⇔ \[\left| {\overrightarrow {OA} - \overrightarrow {OC} + \overrightarrow {OB} - \overrightarrow {OC} } \right| = \left| {\overrightarrow {BA} } \right|\]
⇔ \[\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {BA} } \right|\]
⇔ \[\left| {2\overrightarrow {CI} } \right| = AB\]
Hay 2CI = AB
Tức CI = \(\frac{1}{2}AB\)
Do đó tam giác ABC vuông tại C (đường trung tuyến trong tam giác vuông bằng một nửa cạnh huyền).
Câu 97:
Cho tam giác ABC hãy chỉ ra vị trí của điểm M thỏa mãn mỗi trường hợp sau đây:
a) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} \).
b) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
 Xem đáp án
Xem đáp án
a) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} \)
⇔ \[\overrightarrow {MA} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow {BA} \]
⇔ \[\overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow {BA} \]
⇔ \[\overrightarrow {MC} = \overrightarrow 0 \]
Suy ra: M trùng với C
b) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
⇔ \(\overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \)
⇔ \(\overrightarrow {BA} = - \overrightarrow {MC} = \overrightarrow {CM} \)
Vậy M là đỉnh còn lại của hình bình hành ABCM.
Câu 98:
Có 8 viên bi trong đó có 1 viên bi nặng hơn sắt. Hỏi số lần tối thiểu cần thực hiện? Nêu rõ cách tìm ra viên bi bằng sắt.
 Xem đáp án
Xem đáp án
Để tìm đc viên bi sắt ta sẽ cân. Số cân tối thiểu để tìm viên bi sắt là 3 lần cân
Lần cân thứ nhất : ta chia mỗi bên cân là 4 viên
Bên nào nặng hơn ta cân tiếp
Lần cân thứ hai : ta chia mỗi bên cân là 2 viên
Bên nào nạng hơn ta cân tiếp
Lần thứ ba : ta chia mỗi bên cân nặng hơn
Bên nào nặng hơn là bi sắt.
Câu 99:
Tìm giá trị lớn nhất của sinx + cosx.
 Xem đáp án
Xem đáp án
sinx + cosx = \(\sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)\)
Ta có: \( - 1 \le \sin \left( {x + \frac{\pi }{4}} \right) \le 1\)
Suy ra: \( - \sqrt 2 \le \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) \le \sqrt 2 \)
Vậy giá trị lớn nhất của sinx + cos x là \(\sqrt 2 \)
Dấu “=” khi \(\sin \left( {x + \frac{\pi }{4}} \right) = 1\)
⇔ \(x + \frac{\pi }{4} = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 100:
Một tập thể gồm 14 người gồm 6 nam và 8 nữ trong đó có An và Bình người ta muốn chọn một tổ công tác gồm 6 người. Tìm số cách chọn tổ sao cho có 1 tổ trưởng 5 tổ viên trong đó An và Bình không đồng thời có mặt.
 Xem đáp án
Xem đáp án
TH1: An và Bình không có mặt trong tổ công tác:
Chọn 6 bạn trong 12 bạn (14 người loại An và Bình)
⇒ có \(C_{12}^6\) cách
TH2: An có trong tổ công tác, Bình không có trong tổ công tác:
Chọn An có 1 cách
Chọn 5 bạn trong 12 người còn lại
⇒ có \(C_{12}^5\) cách
TH3: Bình có trong tổ công tác, An không có trong tổ công tác có \(C_{12}^5\) cách
Trong 1 tổ 6 người có 6 cách chọn ra 1 tổ trưởng
Như vậy có tất cả số cách là: \(\left( {C_{12}^6 + C_{12}^5 + C_{12}^5} \right).6 = 15048\) cách.
Câu 101:
Một cửa hàng thời trang có hình thức khuyến mãi sau: giảm giá 10% cho tất cả các mặt hàng, nếu khách hàng nào mua từ 3 sản phẩm trở lên thì ngoài việc được áp dụng khuyến mãi trên, khách hàng còn được giảm thêm 5% trên tổng giá trị tiền phải trả (đã áp dụng hình thức khuyến mãi lần 1). Anh Bảo đã đến cửa hàng trên mua 2 áo sơ mi với giá niêm yết là 340 000 đồng/1 cái, 2 quần tây với giá niêm yết là 360 000 đồng/1 cái, và một đôi giày giá niêm yết 600 000 đồng/ 1 đôi. Hỏi Anh Bảo đã trả cho cửa hàng bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Tổng số tiền anh cần trả nếu không có giảm giá là:
2 . 340 + 2 . 360 + 600 = 2000 (nghìn đồng)
Tổng số tiền anh cần trả nếu chỉ có giảm giá 10% là:
2000 . (100% − 10%) = 1800 (nghìn đồng)
Tổng số tiền anh cần trả nếu có thêm giảm giá 5% là:
1800 . (100% − 5%) = 1710 (nghìn đồng).
Câu 102:
Một đoàn tàu có 5 toa chở khách với mỗi toa còn ít nhất 5 chỗ trống. Trên sân ga có 5 hành khách chuẩn bị lên tàu. Tính xác suất để có ít nhất 1 toa có nhiều hơn 2 khách lên?
 Xem đáp án
Xem đáp án
Số phần tử không gian mẫu: n(Ω) = 55 = 3125.
Gọi A là biến cố: “Có ít nhất 1 toa có nhiều hơn 2 khách lên”.
Có 4 trường hợp:
TH1: Một toa có 3 khách lên, 1 toa có 2 khách lên, 3 toa còn lại không có khách lên
– Chọn 1 toa có 3 khách lên: có \(C_5^1\) cách;
– Chọn 3 khách lên toa vừa chọn: có \(C_5^3\) cách;
– Chọn 1 toa cho 2 khách còn lại: có \(C_4^1\) cách;
Trường hợp này có: \(C_5^1.C_5^3.C_4^1\)= 200 cách.
TH2:1 toa có 3 khách lên, 2 toa có 1 khách, 2 toa còn lại không có khách lên
– Chọn 1 toa có 3 khách lên: có \(C_5^1\) cách;
– Chọn 3 khách lên toa vừa chọn: có \(C_5^3\) cách;
– Chọn 2 toa cho 2 khách còn lại: có \(A_4^2\) cách;
Trường hợp này có: \(C_5^1.C_5^3.A_4^2 = 600\) cách.
TH3:1 toa có 4 khách lên, 1 toa có 1 khách, 3 toa còn lại không có khách lên
– Chọn 1 toa có 4 khách lên: có \(C_5^1\) cách;
– Chọn 4 khách lên toa vừa chọn: có \(C_5^4\) cách;
– Chọn 1 toa cho 1 khách còn lại: có \(C_4^1\) cách;
Trường hợp này có: \(C_5^1.C_5^4.C_4^1\)=100 cách.
TH4:1 toa có 5 khách lên, 4 toa còn lại không có khách lên
Trường hợp này có: \(C_5^1\)= 5 cách.
Số phần tử của biến cố A: n(A) = 200 + 600 + 100 + 5 = 905.
Vậy xác suất của biến cố A là: P(A) \( = \frac{{905}}{{3125}} = \frac{{181}}{{625}}.\)
Câu 103:
Một hình chữ nhật có diện tích 15m2. Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là?
 Xem đáp án
Xem đáp án
Gọi x(m) là chiều rộng, y(m) là chiều rộng.
Theo đề ra: ab = 15
Tăng chiều dài 2 lần, chiều rộng 3 lần thì diện tích mới bằng:
3x.2y = 6xy = 6.15 = 90 (m2).
Câu 104:
Quãng sông từ bến A đến bến B là 24 km. Một chiếc thuyền xuôi dòng từ A đến B hết 1,5 giờ và ngược dòng từ B đến A hết 2,4 giờ. Hỏi cụm bèo trôi từ bến A đến bến B hết bao nhiêu thời gian?
 Xem đáp án
Xem đáp án
Vận tốc thuyền khi xuôi dòng là:
24 : 1,5 = 16 (km/giờ)
Vận tốc thuyền khi ngược dòng là:
24 : 2,4 = 10(km/giờ)
Vận tốc cụm bèo khi trôi là:
(16 − 10) : 2 = 3 (km/giờ)
Thời gian cụm bèo trôi là:
24 : 3 = 8 (giờ).
Câu 105:
Tìm số hạng chứa x3 trong khai triển \({\left( {x - \frac{2}{{{x^2}}}} \right)^n}\) biết n là một số tự nhiên thỏa mãn \(\frac{1}{{A_2^2}} + \frac{1}{{A_2^2}} + ... + \frac{1}{{A_n^2}} = \frac{8}{9}\).
 Xem đáp án
Xem đáp án
Ta có: \(\frac{1}{{A_n^2}} = \frac{1}{{n\left( {n - 1} \right)}} = \frac{1}{n} - \frac{1}{{n - 1}}\)
Suy ra: \(\frac{1}{{A_2^2}} + \frac{1}{{A_2^2}} + ... + \frac{1}{{A_n^2}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{n - 1}} - \frac{1}{n} = \frac{8}{9}\)
⇒ \(1 - \frac{1}{n} = \frac{8}{9}\)
⇒ n = 9.
Lại có: \({\left( {x - \frac{2}{{{x^2}}}} \right)^n} = \sum\limits_{k = 0}^n {C_n^k.{x^k}.{{\left( {\frac{{ - 2}}{{{x^2}}}} \right)}^{n - k}} = } \sum\limits_{k = 0}^n {C_n^k.{x^{3k - 2n}}.{{\left( { - 2} \right)}^{n - k}}} \)
Để có số hạng x3 thì 3k – 2n = 3
Suy ra: 3k – 2.9 = 3
Hay k = 7
Vậy số hạng chứa x3 là: \(C_9^7.{\left( { - 2} \right)^2}.{x^3} = 144{x^3}\).
Câu 106:
Phân tích đa thức thành nhân tử: x2 – 5x + 5y – y2.
 Xem đáp án
Xem đáp án
x2 – 5x + 5y – y2
= (x – y)(x + y) – 5(x – y)
= (x – y)(x + y – 5).
Câu 107:
Tính nhanh : –72. 17 + 72.31 – 36.2.28.
 Xem đáp án
Xem đáp án
–72. 17 + 72.31 – 36.228
= –72. 17 + 72.31 – 36.2.114
= –72. 17 + 72.31 – 72.114
= 72(–17 + 31 – 114)
= 72. (–100)
= –7200.
Câu 108:
 Xem đáp án
Xem đáp án
11 + (– 13) + 15 + (– 17) + ...... + 59 + (–61)
= (–2) + (–2) + … + (–2)
= (–2) . 13
= –26.
Câu 109:
 Xem đáp án
Xem đáp án
2x(x – 4)2 – (x + 5)(x – 2)(x + 2) + 2(x + 5)2 – (x – 1)2
= 2x(x2 – 8x + 16) – (x + 5)(x2 – 4) + 2(x2 + 10x + 25) – (x2 – 2x + 1)
= 2x3 – 16x2 + 32x – x3 + 4x – 5x2 + 20 + 2x2 + 20x + 50 – x2 + 2x – 1
= x3 – 20x2 + 58x + 69.
Câu 110:
Tìm x biết: 42 . x = 15,12.
 Xem đáp án
Xem đáp án
42 . x = 15,12
⇔ x = 15,12 : 42
⇔ x = 0,36
Vậy x = 0,36.Câu 111:
B mua một con bò giá 10 triệu, bán 12 triệu. Vì tiếc nên B mua lại giá 15 triệu, rồi bán được 17 triệu. Vậy B lãi hay lỗi bao nhiêu?
 Xem đáp án
Xem đáp án
B mua bò hết tổng số vốn là:
10 + 15 = 25 (triệu)
B bán bò được số tiền là:
12 + 17 = 29 (triệu)
Vậy B lãi số tiền:
29 – 25 = 4 (triệu).
Câu 112:
Cho biểu thức: \(C = \frac{x}{{2x - 2}} + \frac{{{x^2} + 1}}{{2 - 2{x^2}}}\).
a) Tìm ĐKXĐ.
b) Rút gọn C.
c) Tìm x để \(C = \frac{{ - 1}}{2}\).
 Xem đáp án
Xem đáp án
a) ĐKXĐ: \(\left\{ \begin{array}{l}2x - 2 \ne 0\\2 - 2{x^2} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\{x^2} \ne 1\end{array} \right. \Leftrightarrow x \Leftrightarrow \pm 1\)
b) \(C = \frac{x}{{2x - 2}} + \frac{{{x^2} + 1}}{{2 - 2{x^2}}}\)
\(C = \frac{x}{{2\left( {x - 1} \right)}} + \frac{{{x^2} + 1}}{{2\left( {1 - {x^2}} \right)}}\)
\(C = \frac{{x\left( {x + 1} \right) - {x^2} - 1}}{{2\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\(C = \frac{{x - 1}}{{2\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\(C = \frac{1}{{2\left( {x + 1} \right)}}\)
c) Để \(C = \frac{{ - 1}}{2}\) thì \(\frac{1}{{2\left( {x + 1} \right)}} = \frac{{ - 1}}{2}\)
Suy ra: x + 1 = – 1
Hay x = –1 – 1 = –2
Vậy x = –2 thì \(C = \frac{{ - 1}}{2}\)
Câu 113:
Cho 2 vectơ \(\overrightarrow a ,\overrightarrow b \) thỏa mãn: \(\left| {\overrightarrow a } \right| = 4;\left| {\overrightarrow b } \right| = 3;\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi α là góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \). Tìm cosα?
 Xem đáp án
Xem đáp án
Ta có: \(\left| {\overrightarrow a - \overrightarrow b } \right| = 4 \Rightarrow {\left| {\overrightarrow a - \overrightarrow b } \right|^2} = 16\)
⇒ \({\overrightarrow a ^2} + {\overrightarrow b ^2} - 2\overrightarrow a \overrightarrow b = 16\)
⇒ \[2\overrightarrow a .\overrightarrow b = {\overrightarrow a ^2} + {\overrightarrow b ^2} - 16 = {4^2} + {3^2} - 16 = 9\]
⇒ \[\overrightarrow a .\overrightarrow b = \frac{9}{2}\]
Suy ra: \[\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{\frac{9}{2}}}{{3.4}} = \frac{3}{8}\].
Câu 114:
Cho 2 hàm số y = (k – 2)x + k và y = (k + 3)x – k. Với giá trị nào của k thì đồ thị của 2 hàm số cắt nhau tại 1 điểm:
a) Trên trục tung.
b) Trên trục hoành.
 Xem đáp án
Xem đáp án
a) Cắt nhau tại 1 điểm trên trục tung
⇔ x = 0
⇔ k = −k
b) Cắt nhau tại 1 điểm trên trục hoành
⇔ x = x'
⇒ (k − 2)x + k = 0
⇔ −(k − 2)x = k
⇔ (k + 3)x = −(k − 2)x
⇔ k + 3 = 2 − k
Câu 115:
Cho hình vuông ABCD có AC cắt BD tại O. Gọi E và F theo thứ tự là các điểm đối xứng với O qua AD và BC.
a) Chứng minh rằng các tứ giác AODE,BOCF là hình vuông.
b) Nối EC cắt DF tại I. Chứng minh rằng OI ⊥ CD.
c) Biết diện tích hình lục giác ABFCDE = 6 .Tính độ dài các cạnh của hình vuông ABCD.
d) Lấy K là 1 điểm bất kì trên BC. Gọi G là trọng tâm của tam giác AIK. Chứng minh G thuộc 1 đường thẳng cố định khi K di chuyển trên BC.
 Xem đáp án
Xem đáp án
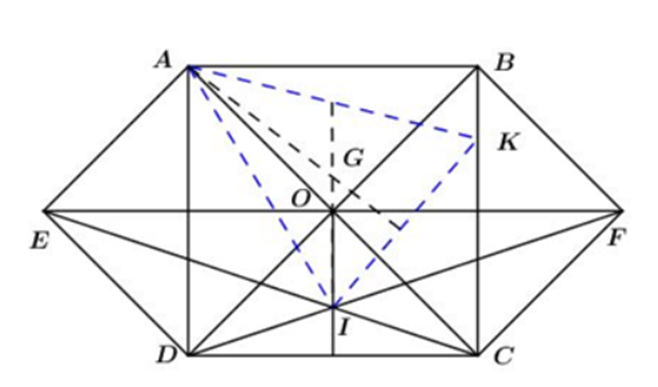
a) Gọi giao điểm của AD và EO là T
Giao điểm của BC và OF là H
Xét tứ giác EAOD có
\(\left\{ \begin{array}{l}AT = TD\\ET = TO\end{array} \right.\) ⇒ EAOD là hình bình hành
Mà AD⊥EO nên tứ giác EAOD là hình thoi.
Hình thoi EAOD có \(\widehat {AOD} = 90^\circ \)nên là hình vuông.
Vậy EAOD là hình vuông theo dấu hiệu nhận biết hình thoi có 1 góc vuông.
Chứng minh tương tự với tứ giác OBFC.
b) Xét 2 tam giác ECF và FDE có:
\(\widehat {CFE} = \widehat {DEF} = 45^\circ \)
EF chung
FC = DE
Nên: ∆ECF = ∆FDE (c.g.c)
Suy ra: \(\widehat {FEC} = \widehat {EFD}\)
Vậy tam giác EFI cân
Mà O là trung điểm của EF ⇒ OI ⊥ EF
c) Ta có:
ΔAED = ΔABO = ΔBCO = ΔCOD = ΔDOA = ΔBFC
SΔAED + SΔABO + SΔBCO + SΔCOD + SΔDOA + SΔBFC = SABCDFE = 6
Suy ra: SΔABO = SΔBCO = SΔCOD = SΔDOA = 1
SABCD = SΔABO + SΔBCO + SΔCOD + SΔDOA = 4
AB = BC = CD = AD = 2
d) Gọi M là giao điểm của IO với AB, N là giao điểm của IM cới AK, ta có:
IO ⊥ FE ⇒ IO ⊥ AB
⇒ OM ⊥ AB, mà O là trung điểm của của HT nên M là trung điểm của AB.
Xét tam giác ABK có:
MA = MB(cmt)
MN // BK (vì MO//CD)
Do đó NA = NK là trung điểm của AK⇒ IN là đường trung tuyến của ΔAIK.
Mà G là trọng tậm tam giác nên G ∈ IN ⇒ G ∈ IM với IM cố định (I,M cố định).
Vậy điểm G luôn nằm trên đường thẳng cố định IM.
Câu 116:
Cho tam giác ABC cân tại A có \(\widehat A = 70^\circ \). Tính các góc \(\widehat B,\widehat C\).
 Xem đáp án
Xem đáp án
Vì tam giác ABC cân tại A nên \(\widehat B = \widehat C\)
Lại có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)
Hay \(70^\circ + 2\widehat B = 180^\circ \)
Suy ra: \(\widehat B = \left( {180^\circ - 70^\circ } \right):2 = 55^\circ \)
Vậy \(\widehat B = \widehat C = 55^\circ \).
Câu 117:
Cho đường thẳng d cắt đường tròn (O;R) tại 2 điểm C, D. M là 1 điểm thuộc d và nằm ngoài (O;R) (MC < MD). Vẽ 2 tiếp tuyến MA, MB với (O;R). H là trung điểm của CD. Đường thẳng AB cắt OH tại E. Chứng minh ED là tiếp tuyến của (O; R).
 Xem đáp án
Xem đáp án
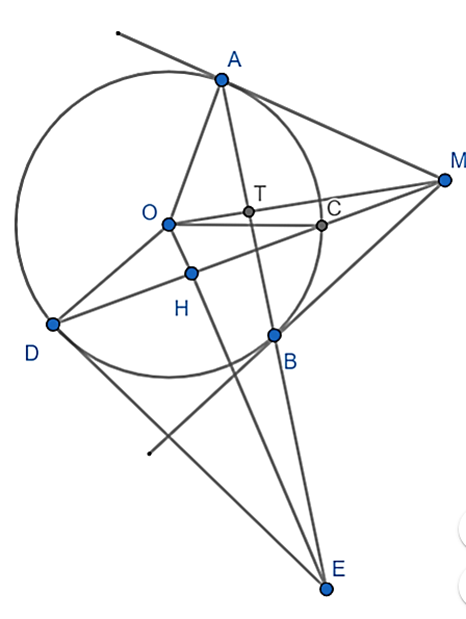
Ta có: MA, MB là tiếp tuyến của (O)
Nên MA = MB và MO là phân giác \(\widehat {AMB}\)
Suy ra: MO vuông góc AB
Gọi H là trung điểm DC; T là giao điểm AE và OM
Suy ra: OH vuông góc DC. OT vuông góc AB (tính chất)
Xét tam giác OHM và tam giác OTE có:
Chung \(\widehat O\)
\(\widehat {OTE} = \widehat {OHM} = 90^\circ \)
⇒ ∆OTE ∽ ∆OHM (g.g)
⇒ \(\frac{{OH}}{{OT}} = \frac{{OM}}{{OE}}\)
⇒ OH.OE = OM.OT
Tam giác AOM vuông tại A có AT là đường cao nên OA2 = OT.OM
Mà OA = OD nên OD2 = OT.OM = OH.OE
⇒ \(\frac{{OD}}{{OH}} = \frac{{OE}}{{OD}}\)
Xét ∆ODH và ∆OED có:
\(\frac{{OD}}{{OH}} = \frac{{OE}}{{OD}}\)
\(\widehat {DOH}\)chung
⇒ ∆ODH ∽ ∆OED (g.g)
⇒ \(\widehat {ODE} = \widehat {OHD} = 90^\circ \)
⇒ OD vuông góc ED tại D
Vậy ED là tiếp tuyến (O).
Câu 118:
Tìm đường thẳng d biết nó cắt đường thẳng d1: y = 2x + 5 tại điểm có hoành độ bằng –2 và cắt đường thẳng d2: y =–3x + 4 tại điểm có tung độ bằng –2.
 Xem đáp án
Xem đáp án
(d):y = ax + b (d) cắt (d1) tại điểm có hoành độ x1 = −2
⇒ y1 = 2.x1 + 5 = 2.(−2) + 5 = 1
(d) cắt (d2) tại điểm có tung độ:
y2 = −2 ⇒ −2 = −3.x2 + 4 ⇒ x2 = 2
Tọa độ 2 điểm đó thỏa mãn phương trình (d)
Nên: \(\left\{ \begin{array}{l}1 = - 2a + b\\ - 2 = 2a + b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{{ - 3}}{4}\\b = \frac{{ - 1}}{2}\end{array} \right.\)
Vậy phương trình đường thẳng là (d): \(y = \frac{{ - 3}}{4}x - \frac{1}{2}\).
Tọa độ của 2 điểm đó thỏa mãn phương trình đường thẳng (d)
Câu 119:
Mua 5kg đường phải trả 85000 đồng. Hỏi mua 3,5kg đường cùng loại phải trả ít hơn bao nhiêu tiền ?
 Xem đáp án
Xem đáp án
1kg phải trả số tiền là:
85000 : 5 = 17000 (đồng)
Mua 3,5kg đường phải trả số tiền là:
17000 . 3,5 = 59500 (đồng)
Mua 3,5kg đường cùng loại phải trả ít hơn số tiền là:
85000 – 59500 = 25500 (đồng).
Câu 120:
Một người dự định sửa nền và lát gach 60cm x 60cm. Biết rằng kích thước nền nhà là 4,8m x 15m, giá tiền 1m ² gạch là 160 000 đồng.
a) Tính số tiền mua gạch?
b) Uớc lượng một viên gach giá bao nhiêu?
 Xem đáp án
Xem đáp án
a) Diện tích nền:
4,8 . 15 = 72 (m2)
Số tiền mua gạch:
72 . 16 000 = 1152000 (đồng)
b) Diện tích mỗi viên gạch:
60 .60 = 3600 cm2 = 3.6 m2
Số viên gạch cần để lót 72 m2 là:
72 : 3.6 = 20 (viên)
b) Vậy giá 1 viên là:
1152000 : 20 = 57600 (đồng /viên).
Câu 121:
 Xem đáp án
Xem đáp án
\[\int {{{\left( {1 + \sin x} \right)}^2}dx = \int {\left( {1 + 2\sin x + {{\sin }^2}x} \right)dx = \int {\left( {1 + 2\sin x + \frac{{1 - \cos 2x}}{2}} \right)dx} } } \]
\[ = \frac{3}{2}x - 2\cos x - \frac{1}{4}\sin 2x + C\]
Lại có: \(F\left( {\frac{\pi }{2}} \right) = \frac{{3\pi }}{4} \Leftrightarrow \frac{3}{2}.\frac{\pi }{2} - 2\cos \frac{\pi }{2} + \frac{1}{4}\sin \pi + C = \frac{{3\pi }}{4}\)
⇔ C = 0
Vậy F(x) = \[ = \frac{3}{2}x - 2\cos x - \frac{1}{4}\sin 2x\].
Câu 123:
Rút gọn biểu thức: \(B = {\sin ^2}32^\circ - \frac{{2022.\tan 51^\circ }}{{\cot 39^\circ }} + {\sin ^2}58^\circ \).
 Xem đáp án
Xem đáp án
\(B = {\sin ^2}32^\circ - \frac{{2022.\tan 51^\circ }}{{\cot 39^\circ }} + {\sin ^2}58^\circ \)
\(B = {\sin ^2}32^\circ - \frac{{2022.\tan 51^\circ }}{{\tan 51^\circ }} + {\cos ^2}32^\circ \)
\(B = \left( {{{\sin }^2}32^\circ + {{\cos }^2}32^\circ } \right) - 2022\)
B = 1 – 2022
B = –2021.
Câu 124:
Tìm x biết: 5x(x – 3) = 5x2 + 7x – 5.
 Xem đáp án
Xem đáp án
5x(x – 3) = 5x2 + 7x – 5
⇔ 5x2 – 15x – 5x2 – 7x + 5 = 0
⇔ –22x = –5
⇔ \(x = \frac{{ - 5}}{{ - 22}} = \frac{5}{{22}}\)
Vậy \(x = \frac{5}{{22}}\).
Câu 125:
Cho biểu thức: \(A = \frac{{x - 3}}{x} - \frac{x}{{x - 3}} + \frac{9}{{{x^2} - 3x}}\).
a) Rút gọn A.
b) Tìm x để A = –3.
 Xem đáp án
Xem đáp án
a) ĐKXĐ: \(\left\{ \begin{array}{l}x \ne 0\\x \ne 3\end{array} \right.\)
\(A = \frac{{x - 3}}{x} - \frac{x}{{x - 3}} + \frac{9}{{{x^2} - 3x}}\)
\(A = \frac{{\left( {x - 3} \right)\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}} - \frac{{{x^2}}}{{x\left( {x - 3} \right)}} + \frac{9}{{x\left( {x - 3} \right)}}\)
\(A = \frac{{{x^2} - 6x + 9 - {x^2} + 9}}{{x\left( {x - 3} \right)}}\)
\(A = \frac{{ - 6x + 18}}{{x\left( {x - 3} \right)}}\)
\(A = \frac{{ - 6\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}}\)
\(A = \frac{{ - 6}}{x}\)
b) Để A = – 3 thì \(\frac{{ - 6}}{x} = - 3 \Leftrightarrow x = 2\).
Câu 126:
Tìm x biết: x.(2013 – x) = 2013.2011 + 2013.
 Xem đáp án
Xem đáp án
x.(2013 – x) = 2013.2011 + 2013
⇔ 2013x – x2 – 2013.2011 – 2013 = 0
⇔ – x2 + 2013x – 2013.2012 = 0
Xét: ∆ = 20132 – 4.(–1).(–2013.2012) > 0 với mọi x
Nên phương trình vô nghiệm.
Câu 127:
Tính giá trị biểu thức: (–15 – 25) : (–5) + (–13).3.
 Xem đáp án
Xem đáp án
(–15–25) : (–5) + (–13).3
= (–40) : (–5) + –39
= –8 + –39
= –47.
Câu 128:
Tính nhanh – (– 2012 + 789) + (– 211) + (– 1012 – 1789).
 Xem đáp án
Xem đáp án
– (– 2012 + 789) + (– 211) + (– 1012 – 1789)
= 2012 – 789 – 211 – 1012 – 1789
= ( 2012 – 1012 ) – 789 – 1789 – 211
= 1000 – 211 – 789 – 1789
= 789 – 789 – 1789
= 0 – 1789
= – 1789.
Câu 129:
Cho hình thang cân ABCD (AB//CD) điểm E là trung điểm của AB. Gọi I, K, M lần lượt là trung điểm của BC, CD, DA.
a) Tứ giác EIKM là hình gì?
b) Tìm điều kiện của hình thang ABCD để EIKM là hình vuông.
 Xem đáp án
Xem đáp án
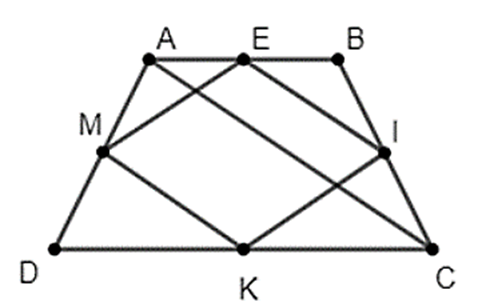
a) Xét tam giác ABC có E; I lần lượt là trung điểm của AB và BC.
Suy ra ta có EI là đường trung bình của tam giác ABC.
Do đó EI // AC, EI = \(\frac{1}{2}AC\) (1)
Chứng minh tương tự ta có: MK // AC, MK = \(\frac{1}{2}AC\)(2)
ME // BD, ME = \(\frac{1}{2}BD\) (3)
Mặt khác AC = BD (do tứ giác ABCD là hình thang cân) (4)
Từ (3) và (4) suy ra ME = MK (5)
Từ (1); (2); (5) suy ra tứ giác EIKM là hình thoi.
b) Để tứ giác EIMK là hình vuông thì EM ⊥ EI.
Mà theo câu a) ta có: EI // AC; EM // BD.
Khi đó suy ra để tứ giác EIMK là hình vuông thì AC ⊥ BD.
Câu 130:
Cho M(4; 1); (d) là đường thẳng luôn đi qua M và cắt Ox, Oy theo thứ tự tại A(a; 0); B(0; b). Hãy viết phương trình đường thẳng (d) sao cho SOAB = 2.
 Xem đáp án
Xem đáp án
Đường thẳng AB đi qua A(a; 0); B(0; b) nên có phương trình: \(\frac{x}{a} + \frac{y}{b} = 1\).
M(4; 1) thuộc AB nên \(\frac{4}{a} + \frac{1}{b} = 1\) (1).
Tam giác AOB vuông tại O nên có diện tích là:
SOAB = \(\frac{1}{2}.OA.OB = \frac{1}{2}ab = 2\). Suy ra: ab = 4. (2).
Từ (1) và (2) ta có:
\(\left\{ \begin{array}{l}\frac{4}{a} + \frac{1}{b} = 1\\ab = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4b + a = ab\\ab = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4 - 4b\\b\left( {4 - 4b} \right) - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4 - 4b\\ - 4{b^2} + 4b - 4 = 0\end{array} \right.\)
⇔ \(\left\{ \begin{array}{l}a = 4 - 4b\\ - \left( {4{b^2} - 4b + 4} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4 - 4b\\ - \left( {4{b^2} - 4b + 4} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4 - 4b\\ - {\left( {2b - 1} \right)^2} - 3 = 0\end{array} \right.\).
Ta thấy –(2b – 1)2 – 3 ≤ – 3 với mọi b nên phương trình –(2b – 1)2 – 3 = 0 vô nghiệm.
Vậy không có đường thẳng (d) thỏa mãn.
Câu 131:
Cho đường tròn (O;R) đường kính AB. Vẽ tiếp tuyến Bx của (O). Trên cùng 1 nửa mặt phẳng bờ AB có chứa Bx, lấy điểm M thuộc (O) (M khác A và B) sao cho MA > MB. Tia AM cắt Bx tại C. Từ C kẻ tiếp tuyến thứ hai CD với (O) (D là tiếp điểm)
a) Chứng minh OC ⊥ BD.
b) Chứng minh bốn điểm O, B, C, D cùng thuộc một đường tròn.
c) Chứng minh \(\widehat {CMD} = \widehat {CDA}\).
d) Kẻ MH vuông góc với AB tại H. Tìm vị trí của M để chu vi tam giác OMH đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án

a) Ta có : CD, CB là tiếp tuyến của (O) ⇒ CO ⊥ BD
b) Vì CD, CB là tiếp tuyến của (O) ⇒ CD ⊥ OD, CB ⊥ OB
⇒ O, B, C, D cùng thuộc đường tròn đường kính OC
c) Ta có : CD là tiếp tuyến của (O)
(góc nội tiếp cùng chắn cung DM)
Xét tam giác CDM và tam giác CAD có:
\(\widehat {CDM} = \widehat {CAD}\)
Chung \(\widehat C\)
⇒ ∆CDM ∽ ∆CAD (g.g)
⇒ \(\widehat {CMD} = \widehat {CDA}\)
d) Ta có :
POMH = OM + MH + HO = R + MH + HO
→Để POMH lớn nhất
→ MH + HO lớn nhất
Mà MH + HO = \(\sqrt {{{\left( {MH + HO} \right)}^2}} \le \sqrt {2\left( {M{H^2} + H{O^2}} \right)} = \sqrt {2{R^2}} = R\sqrt 2 \)
MH + HO lớn nhất khi MH = OH
Suy ra: \(\widehat {MOH} = 45^\circ \Rightarrow \widehat {MOB} = 45^\circ \).