Nếu ô tô đó đi quãng đường 1 km thì tiêu thụ hết số lít xăng là:

12 : 100 = 0,12 (lít)

Nếu ô tô đó đi quãng đường 50 km thì tiêu thụ hết số lít xăng là:

0,12 × 50 = 6 (lít)

Đáp số: 6 lít xăng.

1 lít xăng đi được số km là:

150 : 12 = 12,5 (km)

Nếu xe tiêu thụ hết 16 lít xăng thì đi được số km là:

12,5 × 16 = 200 (km)

Đáp số: 200 km.

Tổng số người của đơn vị đó sau khi được bổ sung thêm là: 

20 + 30 = 50 (người)

Chiều dài của đoạn đường mà đơn vị đó được giao đắp là: 

800 + 400 = 1200 (m)

Thời gian để 50 người đắp xong một đoạn đường dài 800m là: 

10 × 20 : 50 = 4 (ngày)

Thời gian để 50 người đắp xong một đoạn đường dài 1200m là: 

4 × 1200 : 800 = 6 (ngày)

 Đáp số : 6 ngày.

Gọi số người là a (người)

Theo đề bài ta có:

Khi xếp hàng 20; 25; 30 đều dư 15 ⇒ (a – 15) chia hết cho 20; 25; 30

⇒ (a – 15) thuộc BC(20; 25; 30)

Ta có:

20 = 2² . 5;

25 = 5²;

30 = 2 . 3 . 5

⇒ BCNN(20; 25; 30) = 2² . 5² . 3 = 300

⇒ (a – 15) thuộc B(300)={0; 300; 600; 900; 1200;....}

Mà do khi xếp hàng 41 thì đủ tức là a chia hết cho 41 nên a = 615.

Vậy đơn vị có 615 người.

Chiều dài thửa ruộng đó là:

40 .  $\frac{3}{2}$= 60 (m)

Diện tích thửa ruộng là:

60 . 40 = 2400 (m²)

Người ta thu hoạch được số kg ngô là:

2400 : 100 . 50 = 1200 (kg)

Đổi 1200 kg = 1,2 (tạ)

Đáp số: 1,2 tạ.

12x² + 7x – 12

= 12x² – 9x + 16x – 12

= 3x (4x – 3) + 4(4x – 3)

= (3x + 4)(4x – 3).

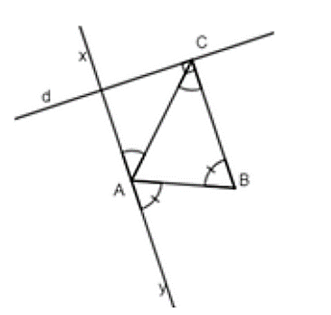
a) Ta có: $\widehat{CAx}=\widehat{ACB}$  mà 2 góc này là góc so le trong nên Ax // BC (1)

$\widehat{BAy}$ =  $\widehat{ABC}$mà 2 góc này là góc so le trong nên Ay // BC (2)

Từ (1) và (2) suy ra: Ax và Ay là hai tia đối nhau nên hai tia này tạo thành một đường thẳng.

b) Lại có tia Ax thuộc mặt phẳng bờ AB có chứa C, tia Ay thuộc mặt phẳng bờ AB không chứa điểm C.

Vì Ax // BC và Ay // BC nên xy // BC

Mà BC ⊥ d nên xy ⊥ d.

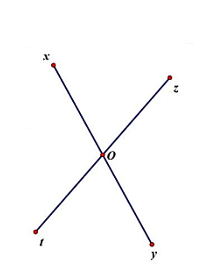
Ta có:$\widehat{xOz}=\widehat{tOy}$ = 70° (2 góc đối đỉnh)

Lại có:$\widehat{xOz}+\widehat{xOt}$  = 180° (2 góc kề bù)

⇒  $\widehat{xOt}$= 180° – 70° = 110°

Mà $\widehat{xOt}$  =  $\widehat{zOy}$ (2 góc đối đỉnh) nên $\widehat{zOy}$ = 110°

Vậy $\widehat{tOy}$  = 70°; $\widehat{xOt}$ = 110°; $\widehat{zOy}$ = 110°.

Nửa chu vi là:

0,8 : 2 = 0,4 (km)

Chiều rộng của mảnh đất đó là:

0,4 : (3 + 5) . 3 = 0,15 (km)

Chiều dài của khu đất đó là:

0,4 – 0,15 = 0,25 (km )

Diện tích mảnh đất đó là:

0,15 . 0,25 = 0,0375 (km²)

Đổi 0,0375 km² = 375 ha

Đổi 30 phút = $\frac{1}{2}$  giờ

Gọi vận tốc xe máy lúc đi từ A đến B là x (km/giờ), với x > 0

Thời gian xe đi từ A đến B là: $\frac{90}{x}$  (giờ)

Vận tốc lúc về BA là x + 9 (km/giờ)

Thời gian về là:$\frac{90}{x+9}$ (giờ)

Ta có phương trình:

$\frac{90}{x}$+$\frac{90}{x+9}$ + $\frac{1}{2}$ = 5

⇔ 40x + 180 = x² + 9x

⇔ x² – 31x – 180 = 0

⇔ $\left[\begin{array}{l}x=36\\ x=-5\end{array}\right.$

Vậy vận tốc xe máy đi từ A đến B là 36 km/giờ.

$\sqrt{x}\sqrt{y}\sqrt{xy}=5$

⇔ $\sqrt{x^2{y}^2}=5$

⇔ xy = 5 (vì x,y > 0).

Mà 5 = 1.5

Nên x = 1; y = 5 hoặc x = 5; y = 1.

Vì  $\overline{87ab}$chia hết cho 9 nên (15 + a + b) phải chia hết cho 9

Mà a = b + 4 nên a ≥ 4

Vì 4 ≤ a + b ≤ 18 ⇒ a + b = 12

Với a + b = 12 kết hợp với a – b = 4

Suy ra: a = 8 và b = 4

Vậy số cần tìm là 84.

Để d song song với Ox thì d phải có dạng by + c = 0 với b, c ≠ 0.

Nên: $\left\{\begin{array}{l}9m^2-4=0\\ n^2-9\ne 0\\ \left(n-3\right)\left(3m+2\right)\ne 0\end{array}\right.$  ⇒    $\left\{\begin{array}{l}m=\pm \frac{2}{3}\\ n\ne \pm 3\\ n\ne 3\\ m\ne \frac{-2}{3}\end{array}\right.$ ⇒ $\left\{\begin{array}{l}m=\frac{2}{3}\\ n\ne \pm 3\end{array}\right.$ .

(5x – 2y)(5x + 2y) + 4y – 1

= 25x² – 4y² + 4y – 1

= 25x² – (4y² – 4y + 1)

= 25x² – (2y – 1)²

= (5x + 2y – 1)(5x – 2y + 1)

Diện tích hình chữ nhật là:

16 . 4,5 = 72 (m²)

Vì diện tích hình vuông bằng diện tích hình chữ nhật nên diện tích hình vuông là 72 m²

Ta thấy 72 = $6\sqrt{2}.6\sqrt{2}$ nên cạnh hình vuông là $6\sqrt{2}$  m

Chu vi hình vuông là:

$6\sqrt{2}$. 4 = $24\sqrt{2}$ (m).

1 dm² = 100 cm²

8 dm² = 800 cm²

Ta có: 8 = 2³

Suy ra: 8 chia hết cho 2; 4

Vậy 8 là hợp số vì nó có nhiều hơn 2 ước (số nguyên tố chỉ chia hết cho 1 và chính nó).

Số kẹo của Bình là:

60 .  $\frac{1}{3}$= 20 (cái).

Số kẹo Bình cho Minh là:

20 .$\frac{1}{4}$ = 5 (cái)

Số kẹo còn lại của Bình là:

20 – 5 = 15 (cái).

Đáp số: 15 cái.

x³ – 3x² + 5x + m

= (x³ – x² + 3x) – (2x² – 2x + 6) + m + 6

= (x – 2)(x² – x + 3) + m + 6

Ta thấy: (x – 2)(x² – x + 3) chia hết cho x – 2 nên để A chia hết cho B thì:

m + 6 = 0 tức m = – 6

Vậy m = – 6.

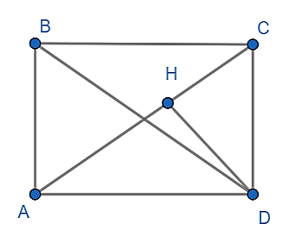
Do ABCD là hình chữ nhật ⇒ CD = AB = 13 cm và BD = AC

Áp dụng định lí Pi–ta–go vào tam giác vuông DHC có:

HC² = CD² – DH² = 13² – 5² = 12² ⇒ HC = 12 cm

Áp dụng hệ thức lượng vào tam giác vuông ACD có:

CD² = HC.AC ⇒ AC = CD² : HC = 169 : 12 = 25 cm

Vậy BD = AC = 25cm.

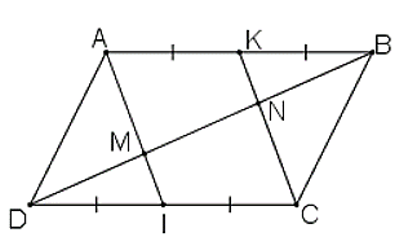
a) ABCD là hình bình hành

⇒ AB // CD ⇒ AB // IC

AB = CD

Mà K, I lần lượt là trung điểm của AB và CD.

⇒AK = IC

Mà AK // IC

⇒ AKIC là hình bình hành

Xét ΔADI và ΔBCKcó:

DI = BK

AI = CK

AD = BC

⇒ ΔADI = ΔBCK (c.c.c)

⇒$\widehat{DAI}=\widehat{BCK}$

Xét ΔADM và ΔCBN có: 

$\widehat{DAI}=\widehat{BCK}$

AD=BC

$\widehat{ADB}=\widehat{DBC}$ ( Do AD//BC)

b) Vì AKIC là hình bình hành ⇒  $\widehat{ADM}=\widehat{NCA}$và IM // CN

c) Xét ΔDCN có: MI // NC, I là trung điểm DC

Nên MI là đường trung bình của ΔDCN

⇒ DM = MN (1)

Xét ΔAMB có AM // KN, K là trung điểm AB

Nên KN là đường trung bình của ΔAMB

⇒ NB = MN (2)

Từ (1) và (2) suy ra: DM = MN = NB.

Hiệu mẫu và tử số là:

13 – 7 = 6

Khi cùng thêm 1 số vào mẫu và tử thì hiệu mẫu và tử vẫn bằng 6

Hiệu số phần bằng nhau là:

3 – 2 = 1 (phần)

Tử mới là:

6 : 1 . 2 = 12

Số cần tìm là:

12 – 7 = 5

Đáp số: 5.

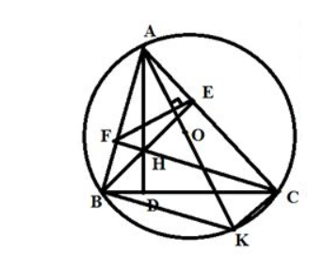
Ta có:$\widehat{CFB}$ =$\widehat{BEC}$ = 90° (Vì BE và CF là đường cao)

Mà 2 góc này cùng thuộc 1 nửa mặt phẳng bờ BC nên tứ giác BFCE nội tiếp.

Số bạn mỗi hàng có là:

36 : 4 = 9 (bạn).

Số hàng 54 bạn xếp được là:

54 : 9 = 6 (hàng).

Đáp số: 6 hàng.

Gọi số lớn là a, số bé là b

Ta có:

a – 14,75 = b + 3,25

Suy ra a – b = 18

Lại có: a + b = 20

Số lớn là:

(20 + 18) : 2 = 19

Số bé là:

20 – 19 = 1.

Ban đầu Hùng có nhiều hơn Dũng:

5 + 5 = 10 (viên bi).

Số viên bi của bạn Hùng là:

(46 + 10) : 2 = 28 (viên bi).

Số viên bi của bạn Dũng là:

46 – 28 = 18 (viên bi).

Đáp số: Hùng: 28 viên bi; Dũng: 18 viên bi.

Xưởng sản xuất nước mắm đã sản xuất được 1230 lít nước mắm.

Mỗi can 2 lít thì cần số can là:

1230 : 2 = 615 (can)

Mỗi can 3 lít thì cần số can là:

1230 : 3 = 410 (can)

Mỗi can 5 lít thì cần số can là:

1230 : 5 = 246 (can)

Vậy ta hoàn thành bảng sau:

Có tất cả số lít xăng là:

2 . 12 = 24 (lít)

Nếu mỗi xe đổ 3 lít thì số xăng đó đủ đổ cho số xe là:

24 : 3 = 8 (xe)

Đáp số: 8 xe.

Đổi 0,8km = 800 m

Nửa chu vi khu đất hình chữ nhật là: 

800 : 2 = 400 (m)

Chiều rộng khu đất hình chữ nhật là:   

400 : (3 + 5) × 3 = 150 (m)

Chiều dài khu đất hình chữ nhật là:   

400 – 150 = 250 (m)

Diện tích khu đất đó là:

250 × 150 = 37500 (m²)

Đổi 37500 m² = 3,75 ha.

Quãng đường ô tô chạy được trong hai giờ đầu là:

46 × 2 = 92 (km)

Quãng đường ô tô chạy được trong hai giờ sau là:

43 × 2 = 86 (km)

Quãng đường từ tỉnh A đến tỉnh B dài là:

92 + 52 + 86 = 230 (km)

Trung bình mỗi giờ ô tô chạy được là:

230 : 5 = 46 (km)

Đáp số: Quãng đường AB: 230 km;

Trung bình mỗi giờ ô tô chạy 46 km

Trong 30 ngày một con sư tử ăn hết số ki–lô–gam thịt là:

9 . 30 = 270 (kg)

Trong 30 ngày 6 con sư tử ăn hết số tấn thịt là:

270 . 6 = 1620 (kg) = 1,62 (tấn)

Đáp số: 1,62 tấn thịt.

Tổng 3 số là:

18 . 3 = 54

Số thứ 2 là:

28 : 2 = 14

Số thứ 3 là:

54 – 28 – 14 = 12

Đáp số: 12.

Tổng hai số là:

34 . 2 = 68.

Số kia là:

68 – 12 = 56.

Đáp số: 56.

3 số khác nhau có 1 chữ số lớn nhất là 7, 8, 9

Vậy giá trị lớn nhất của abc là: 7.8.9 = 504.

Hiệu 2 số là:

44 . 2 + 2 = 90.

Số lớn là:

(110 + 90) : 2 = 100.

Số bé là:

110 – 100 = 10.

Đáp số: số lớn 100; số bé 10.

Vì ở giữa hai số chẵn có 3 số lẻ nên hiệu của hai số chẵn đó là 6. Tổng của chúng là 38.

Vậy số bé là:

(38 − 6) : 2 =16.

Số lớn là:

16 + 6 = 22.

Đáp số: 16 và 22.

Số nữ của xã là:

3600 : (49 + 51) × 51 = 1836 (người).

Số nam của xã là:

3600 – 1836 = 1764 (người).

Số nữ nhiều hơn số nam số người là:

1836 – 1764 = 72 (người).

Đáp số: 72 người.

y = mx – (2m–3).cos x

y' = m + (2m – 3). sin x (1)

Để hàm số đồng biến trên ℝ thì y' ≥ 0 với mọi x thuộc ℝ

Tức: m + (2m – 3). sin x ≥ 0 với mọi x thuộc ℝ

Vì –1 ≤ sin x ≤ 1 nên ta có:

Với 2m−3 ≥ 0 ⇔ m ≥  $\frac{3}{2}$

(1) tương đương với m – (2m – 3) ≥ 0

⇔ m ≤ 3

suy ra $\frac{3}{2}$ ​≤ m ≤ 3.

Với 2m−3 < 0 ⇔ m <$\frac{3}{2}$

(1) tương đương với: m + (2m−3) ≥ 0

⇔ m ≥ 1

suy ra 1 ≤ m < ​$\frac{3}{2}$.

Vậy 1 ≤ m ≤ 3.

(x – 7)(x² – 9x + 20)(x – 2) = 72

⇔ (x² – 9x+ 20)(x² – 9x + 14) – 72 = 0

Đặt x² – 9x + 14 = a

Ta có:

(a + 6)a – 72 = 0

⇔ a² + 6a – 72 = 0

⇔ (a – 6)(a + 12) = 0

⇔$\left[\begin{array}{l}a=6\\ a=-12\end{array}\right.$

Với a = 6 thì x² – 9x + 14 = 6

⇔ x² – 9x + 8 = 0

⇔ (x – 8)(x – 1) = 0

⇔$\left[\begin{array}{l}x=1\\ x=8\end{array}\right.$

Với a = –12 thì x² – 9x + 14 = –12

⇔ x² – 9x + 26 = 0

⇔ ${\left(x-\frac{9}{2}\right)}^2+\frac{23}{4}=0$ (vô lí)

Vậy x = 1 hoặc x = 8.

Theo giả thiết đề bài cho, ta có biểu đồ Ven:

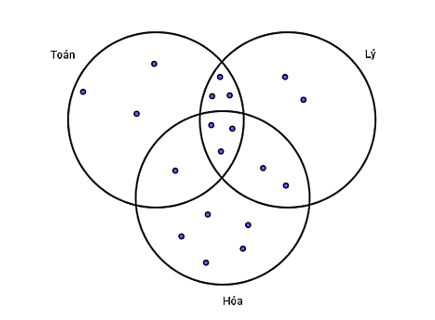
Dựa vào biểu đồ Ven ta thấy:

Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 

6 – 3 = 3 (em).

Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 

4 − 3 = 1 (em).

Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 

5 − 3 = 2 (em).

Số học sinh chỉ giỏi một môn Toán là: 

10 – 3 – 3 − 1 = 3 (em).

Số học sinh chỉ giỏi một môn Lý là: 

10 – 3 – 3 − 2 = 2 (em).

Số học sinh chỉ giỏi một môn Hóa là: 

11 – 1 – 3 − 2 = 5 (em).

Số học sinh giỏi ít nhất một trong ba môn là:

3 + 2 + 5 + 1 + 2 + 3 + 3 = 19 (em).

Đổi $\frac{4}{5}$ = 0,8 m.

Diện tích hình chữ nhật là:

16 × 0,8 = 12,8 (m²).

Đáp số: 12,8 m².

A = 4 + 4² + … + 4²⁰

A = (4 + 4²) + (4³ + 4⁴) + … + (4¹⁹ + 4²⁰)

A = 4(1 + 4) + 4³ (1 + 4) + … + 4¹⁹(1 + 4)

A = (1 + 4)(4 + 4³ + … + 4¹⁹)

A = 5 . (4 + 4³ + … + 4¹⁹)

Vì 5 chia hết cho 5 nên 5 . (4 + 4³ + … + 4¹⁹) chia hết cho 5.

Vậy A chia hết cho 5.

Tổng số tuổi 22 bố con hiện nay là:

54 − 2 × 5 = 44 (tuổi).

Tuổi con hiện nay là:

(44 − 26) : 2 = 9 (tuổi).

Tuổi bố hiện nay là:

9 + 26 = 35 (tuổi).

Đáp số: bố: 35 tuổi; con: 9 tuổi.

Chiều rộng thật của mảnh vườn là:

3 × 2500 = 7500 (cm).

Chiều dài thật của mảnh vườn là:

5 × 2500 = 12500 (cm).

Diện tích thật của mảnh vườn là:

7500 × 12500 = 93750000 (cm²).

Đáp số: 93750000 cm².

Để d song song với Ox thì d phải có dạng by + c = 0 với b, c ≠ 0.

Nên: $\left\{\begin{array}{l}9m^2-4=0\\ n^2-9\ne 0\\ \left(n-3\right)\left(3m+2\right)\ne 0\end{array}\right.$  ⇒   $\left\{\begin{array}{l}m=\pm \frac{2}{3}\\ n\ne \pm 3\\ n\ne 3\\ m\ne \frac{-2}{3}\end{array}\right.$  ⇒ $\left\{\begin{array}{l}m=\frac{2}{3}\\ n\ne \pm 3\end{array}\right.$ .

Chiều dài mảnh vải hình chữ nhật là:

(120 + 20) : 2 = 70 (cm)

Chiều rộng mảnh vải hình chữ nhật là:

(120 – 20) : 2 = 50 (cm)

Diện tích mảnh vải hình chữ nhật là:

70 × 50 = 3500 (cm²)

Đáp số: 3500 cm².

1,8 tạ = 180 kg

1 năm = 12 tháng

Trung bình mỗi tháng nhà em ăn hết là :

180 : 12 = 15 (kg).

Đáp án: 15 kg.

Ta có:

 EB // FD

⇒AE // FD (1)

Từ tia đối của tia EK vẽ KD // AE

Lại có: EK và KD cùng song song với FA

⇒ ED song song với FA (2)

Từ (1) và (2) suy ra AFDE là hình bình hành.

⇒ AD giao EF tại trung điểm mỗi đường

⇒ I là trung điểm của EF

⇒ IE = IF (*)

EK ⊥ AB

FA ⊥AB

⇒ FA // EK

⇒$\widehat{KEI}=\widehat{CFI}$

 Xét tam giác EKI và tam giác FCI có :

$\widehat{KEI}=\widehat{CFI}$ (chứng minh trên)

IE = IF ( chứng minh * )

$\widehat{KIE}=\widehat{CIF}$ ( hai góc đối đỉnh bằng nhau )

⇒ ∆EKI = ∆FCI ( g.c.g )

⇒ EK = CF

Mà BE = CF

⇒ BE = EK

Mà lại có:  vuông

⇒ Tam giác BEK là tam giác vuông cân tại E.

N = (x – y)(x – 2y)(x – 3y)(x – 4y) + y⁴

N = [(x – y)(x – 4y)][(x – 2y)(x – 3y)] + y⁴

N = (x² – 5xy + 4y²)(x² – 5xy + 6y²) + y⁴

Đặt x² – 5xy + 5y² = a, ta được:

N = (a – y²)(a + y²) + y⁴

N = a² – y⁴ + y⁴

N = a²

N = (x² – 5xy + 5y²)²

Vậy N là số chính phương.

Thời gian người đi xe máy đi từ A đến chỗ nghĩ là:

7 giờ 15 phút – 6 giờ 30 phút = 45 phút

Đổi 45 phút = 0,75 giờ.

Quãng đường người đó đi được từ A đến chỗ nghỉ là:

36 . 0,75 = 27 (km).

Quãng đường còn lại người đó phải đi là:

75 – 27 = 48 (km).

Thời gian người đó đi từ chỗ nghỉ đến B là:

48 : 40 = 1,2 (giờ).

Đổi 1,2 giờ = 1 giờ 12 phút

Thời gian người đó đi từ A đến B (tính cả thời gian nghỉ là):

45 phút + 10 phút + 1 giờ 12 phút = 2 giờ 7 phút.

Người đó đến B lúc:

6 giờ 30 phút + 2 giờ 7 phút = 8 giờ 37 phút.

Mỗi lít sữa nặng là:

0,78 : 0,75 = 1,04 (kg)

Số lít sữa nặng 26 kg là:

26 : 1,04 = 25 (lít)

Đáp số: 25 lít.

A = 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + 9 + ... + 2018 – 2019 – 2020 + 2021 – 2022 + 2023

A = (1 + 2 – 3 – 4) + (5 + 6 – 7 – 8) + … + (2017 + 2018 – 2019 – 2020) + 2021 – 2022 + 2023

A = (–4) + (–4) + … + (–4) + 2021 – 2022 + 2023

A = (–4) . 505 + 2021 + 1

A = (–2020) + 2021 + 1

A = 2.

Vậy A = 2.

x(x – y)³ – y(y – x)² – y²(x – y)

= x(x – y)³ – y(x – y)² – y²(x – y)

= (x – y)[x(x – y)² – y(x – y) – y²]

= (x – y)(x³ – 2x²y + y²x – xy )

= x(x – y)(x² – 2xy + y² – y)

= x(x – y)[(x – y)² – y]

= x(x – y)(x – y – )(x – y + ).

Số thứ ba là:

62,2 – 53,15 = 9,05

Số thứ nhất là:

9,05 + 6,85 = 15,9

Số thứ hai là:

53,15 – 15,9 = 37,25

Đáp số: 37,25.

Vì 308 và 264 đều chia hết cho x và x lớn nhất nên x = ƯCLN(308, 264)

308 = 2² . 7 . 11

264 = 2³ . 3 . 11

ƯCLN (308, 264) = 2² . 11 = 44

Vậy x = 44.

312 : 0,1 = 312 : $\frac{1}{10}$ = 312 × 10 = 3120.

Vì 5 ⋮ (n + 1) nên n + 1 ∈ Ư(5) = {±1; ±5}

Suy ra n ∈ {–2; 0; 4; –6}

Mà n là số tự nhiên nên n = 0 hoặc n = 4.

97345 – 9205 × 3 – 7 × 9205

= 97345 – 9205 × (3 + 7)

= 97345 – 9205 × 10

= 97345 – 92050

= 5295.

Để được số chia hết cho 3 thì tổng các chữ số của nó phải chia hết cho 3.

Các bộ số lập thành số chia hết cho 3 là (5; 6; 7), (5; 7; 9), (6; 7; 8), (7; 8; 9)

Với mỗi bộ số này có thể lập được 3! số

Vậy ta lập được: 4 . 3! = 24 (số).

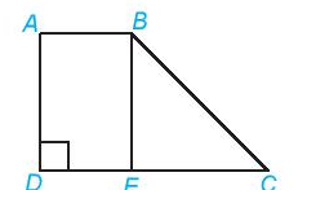
Chiều dài của đoạn AD là:   

150 : 10 = 15 (m)

Diện tích mảnh đất là:     

$\frac{1}{2}$AD. (AB + DC) =  . 15. (10 + 25) = 262,5 (m²)

Vậy diện tích mảnh đất hình thang ABCD là 262,5 m².

Nếu tăng chiều rộng thêm 5m và bớt chiều dài đi 5m thì mảnh đất hình chữ nhật trở thành một mảnh đất hình vuông.Vậy chiều dài hơn chiều rộng là:

5 + 5 = 10 (m).

Nửa chu vi hình chữ nhật là:

120 : 2 = 60 (m).

Chiều rộng hình chữ nhật là:

(60 – 10) : 2 = 25 (m).

Chiều dài hình chữ nhật là:

25 + 10 = 35 (m).

Diện tích hình chữ nhật:

25 . 35 = 875 (m²).

Đáp số: 875 m².

Đổi 2,075 m = 0,002075 km

872 m = 0,872 km

Suy ra:

3,6 km + 2,075 m + 872 m

= 3,6 km + 0,002075 km + 0,872 km

= 4,474075 km.

8x(x – 2017) – 2x + 4034 = 0

⇔ 8x(x – 2017) – 2(x – 2017) = 0

⇔ (x – 2017)(8x – 2) = 0

⇔ $\left[\begin{array}{l}x-2017=0\\ 8x-2=0\end{array}\right.$

⇔ $\left[\begin{array}{l}x=2017\\ x=\frac{1}{4}\end{array}\right.$

Vậy x = 2017 hoặc x =  $\frac{1}{4}$.

Ba tổ thu gom được:

(25,5 + 36,2 + 24,5) : 2 = 43,1 (kg giấy vụn).

Tổ 1 thu gom được:

43,1 – 24,5 = 18,6 (kg giấy vụn).

Tổ 2 thu gom được:

43,1 – 36,2 = 6,9 (kg giấy vụn).

Tổ 3 thu gom được:

43,1 – 25,5 = 17,6 (kg giấy vụn).

Số túi cả hai loại gạo là:

10 + 12 = 22 (túi).

Số ki–lô– gam gạo trong mỗi túi là:

220 : 22 = 10(kg).

Số ki–lô–gam gạo loại 1 là:

10 . 10 = 100 (kg).

Số ki–lô–gam gạo loại 2 là :

220 – 100 = 120 (kg).

Đáp số: Gạo loại 1: 100kg; gạo loại 2: 120 kg.

Diện tích hình vuông hay diện tích hình chữ nhật là:

2 × 8 = 16 (m²).

Vì 16 = 4 × 4 nên cạnh hình vuông là 4 m.

Vậy độ dài cạnh hình vuông là 4 m.

A = 1 + 4 + 4² + … + 4²⁰²¹

A = (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + … + (4²⁰¹⁹ + 4²⁰²⁰ + 4²⁰²¹)

A = (1 + 4 + 4²) + 4³(1 + 4 + 4²) + … + 4²⁰¹⁹ (1 + 4 + 4²)

A = (1 + 4 + 4²)(1 + 4³ + … + 4²⁰¹⁹)

A = 21 . (1 + 4³ + … + 4²⁰¹⁹)

Vì 21 chia hết cho 21 nên 21 . (1 + 4³ + … + 4²⁰¹⁹) chia hết cho 21.

Vậy A chia hết cho 21.

2ax³ + 6ax² + 6ax + 18a

= 2ax² (x + 3) + 6a (x + 3)

= (x + 3)(2ax² + 6a)

= 2a(x + 3)(x² + 3).

Khi gấp một thừa số lên 33 lần thì tích mới gấp lên 33 lần so với tích cũ.

Tích mới có giá trị là:

3648 . 3 = 10944.

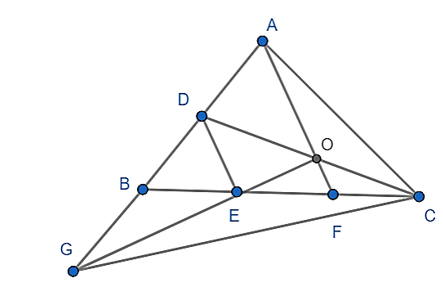
Gọi giao điểm của AF và CD là O.

∆ABF có D, E là trung điểm AB, BF nên DE là đường trung bình của tam giác ABF

⇒ DE // AF hay DE // OF

∆CDE có OF // DE, F là trung điểm CE nên O là trung điểm của CD.

Xét ∆CDG có: CE = $\frac{2}{3}$  CB, CB là đường trung tuyến

Nên E là trọng tâm của ∆CDG

Hay GE đi qua trung điểm CD tức GE đi qua O.

Vậy AF, CD, GE đồng quy tại O.

Số lít dầu có trong thùng thứ hai là:

10,5 + 3 = 13,5 (lít).

Số lít dầu có trong thùng thứ ba là:

(10,5 + 13,55) : 2 = 12 (lít).

Số lít dầu có trong cả ba thùng  là:

10,5 + 13,5 + 12 = 36 (lít).

Đáp số: 36 lít dầu.

Số lẻ lớn nhất có 2 chữ số là 99.

Số lẻ nhỏ nhất có 2 chữ số lớn hơn 15 là 17.

Số các số lẻ thỏa mãn yêu cầu bài toán là:

(99 – 17) : 2 + 1 = 42 (số).

Tổng số tiền người đó có là:

4000 . 30 = 120000 (đồng)

Với số tiền đó mua gạo loại 6000 đồng thì được số kg là:

120000 : 6000 = 20 (kg).

Đáp số: 20 kg.

Tổng số viên bi của hai bạn sau khi thêm 6 viên là:

64 + 6 = 70 (viên).

Số bi của hai bạn sau khi thêm là:

70 : 2 = 35 (viên).

Dũng có số bi là:

35 – 6 = 29 (viên).

Đáp số: Hùng 35 viên; Dũng 29 viên.

Trung bình mỗi ngày cửa hàng bán được số lít xăng là:

(2064 + 945 × 3 ) : 7 = 777 (lít xăng).

Đáp số: 777 lít xăng.

Chu vi hình chữ nhật là:

6 × 4 = 24 (cm)

Nửa chu vi mảnh bìa là:

24 : 2 = 12 (cm)

Chiều dài mảnh bìa là:

(12 + 6) : 2 = 9 (cm).

Chiều rộng mảnh bìa là:

9 – 6 = 3 (cm).

Diện tích mảnh bìa là:

9 × 3 = 27 (cm²).

Đáp số: 27 cm².

3²ⁿ = (3²)ⁿ = 9ⁿ

2³ⁿ = 8ⁿ

Vì 9ⁿ > 8ⁿ nên 3²ⁿ > 2³ⁿ.

199²⁰ < 200²⁰ = (8.25)²⁰ = (2³.5²)²⁰ = 2⁶⁰ . 5⁴⁰

2003¹⁵ > 2000¹⁵ = (16.125)¹⁵ = (4².5³)¹⁵ = 2⁶⁰ . 5⁴⁵

Vì 2⁶⁰ . 5⁴⁰ < 2⁶⁰ . 5⁴⁵ nên 199²⁰ < 2003¹⁵.

Vậy 199²⁰ < 2003¹⁵.

Hiệu số phần bằng nhau là:

19 – 1 = 18 (phần).

Số lớn là:

19,98 : 18 × 19 = 21,09.

Số bé là:

19,98 : 18 × 1 = 1,11.

Gọi số có 2 chữ số cần tìm là $\overline{ab}$  (a ≠ 0; a, b < 10).

Ta có:

23  $\overline{ab}$=  $\overline{1ab1}$

⇔ 23  $\overline{ab}$= 1001 + 10 $\overline{ab}$

⇔ 13  $\overline{ab}$= 1001

⇔ $\overline{ab}$ = 1001 : 13

⇔ $\overline{ab}$ = 77.

Vậy số cần tìm là 77.

Trung bình cộng xe thứ nhất và thứ hai là:

(45 + 53) : 2 = 49 (tạ).

Xe thứ ba chở số tạ hàng là:

49 + 6 = 55 (tạ).

Trung bình cộng 3 xe chở số tạ là:

(45 + 53 + 55) : 3 = 51 (tạ).

Đáp số: 51 tạ.

Ta có: 51 = 1.51 = 3.17 = (–1).(–51) = (–3)(–17)

Vậy các ước của 51 là ±1; ±3; ±17; ±51.

3ax² + 3bx² + ax + bx + 5a + 5b

= 3x²(a + b) + x(a + b) + 5(a + b)

= (a + b)(3x² + x + 5).