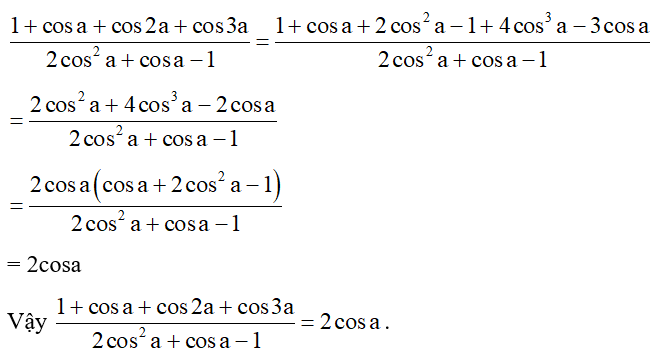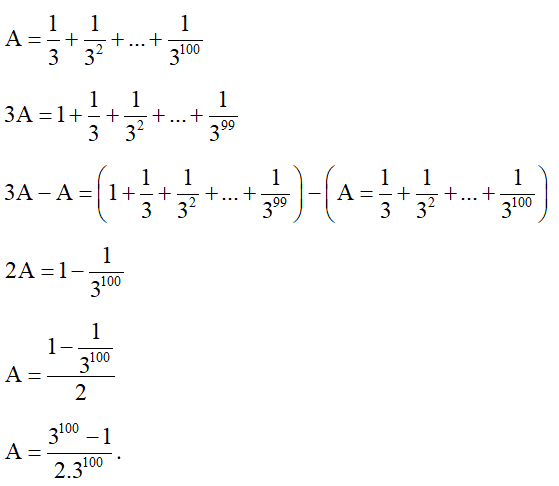- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 92)
-
12888 lượt thi
-
99 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 2:
Cho khu vườn hình chữ nhật có chiều dài là 35m chiều rộng là 20 m.
a) Tính chu vi và diện tích khu vườn.
b) Nếu người ta để lại làm đường đi xung quanh và đường rộng là 2,5 m thì diện tích phần còn lại để trồng rau là bao nhiêu?
 Xem đáp án
Xem đáp án
a) Chu vi khu vườn là:
(35 + 20) . 2 = 150 (m)
Diện tích khu vườn là:
35.20 = 700 (m2)
b) Chiều dài phần trồng rau là:
35 - 2,5 . 2 = 30 (m)
Chiều rộng phần trồng rau là:
20 - 2,5 . 2 = 15 (m)
Diện tích phần trồng rau là:
30 . 20 = 450 (m2).
Câu 3:
Cho hàm số y = ax + 3. Hãy xác định hệ số a trong trường hợp sau:
Đồ thị của hàm số song song với đường thẳng y = -2x.
 Xem đáp án
Xem đáp án
Theo đề bài ta có b ≠ b' (vì 3 ≠ 0)
Vậy đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x khi và chỉ khi a = a' tức là:
a = -2.
Hàm số có dạng y = 2x + 3.
Câu 5:
Các số 0; -8; -0,6 có phải là số hữu tỉ không? Vì sao?
 Xem đáp án
Xem đáp án
Số hữu tỉ là số có thể viết dưới dạng với a,b thuộc ℤ và b # 0 và được kí hiệu là ℚ.
Khi đó: Số 0; -8;-0,6 là các số hữu tỉ.
Câu 6:
Cho A là các số tự nhiên chia hết cho 3 và nhỏ hơn 30; B là tập hợp các só tự nhiên chia hết cho 6 và nhỏ hơn 30; C là tập hợp các số tự nhiên chia hết cho 9 và nhỏ hơn 30.
a) Viết các tập hợp A, B, C bằng cách liệt kê các phần tử của các tập hợp đó.
b) Xác định số phần tử của mỗi tập hợp.
c) Dùng kí hiệu tập hợp con để thể hiện quan hệ giữa các tập hợp đó.
 Xem đáp án
Xem đáp án
a) Ta có:
A = {0; 3; 6; 9; 12; 15; 18; 21; 24; 27}.
B = {0; 6; 12; 18; 24}.
C = {0; 9; 18; 27}.
b) Ta thấy mỗi số hạng thuộc A đều hơn kém nhau 3 đơn vị
Số phần tử của tập hợp A là:
(27 - 0) : 3 + 1 = 10 (phần tử)
Số phần tử của tập hợp B là:
(24 - 0) : 6 + 1 = 5 (phần tử)
Số phần tử của tập hợp C là:
(27 - 0) : 9 + 1 = 4 (phần tử)
c) C ⊂ B ⊂ A.
Câu 7:
Tìm x biết 84 chia hết cho x, 180 chia hết cho x và x ≥ 6.
 Xem đáp án
Xem đáp án
Vì 84 chia hết cho x, 180 chia hết cho x nên x ∈ ƯC(84, 180)
Ta có: 84 = 22.3.7; 180 = 22.32.5
Suy ra: ƯCLN(84, 180) = 22.3 = 12
Nên x ∈ Ư(12) = {1; 2; 3; 4; 6; 12}
Mà x ≥ 6 nên x = 6 hoặc x = 12.
Vậy x = 6 hoặc x = 12.
Câu 8:
Từ 1 đến 100 có bao nhiêu số chia hết cho 4?
 Xem đáp án
Xem đáp án
Số bé nhất trong khoảng từ 1 đến 100 chia hết cho 4 là 4
Số lớn nhất trong khoảng từ 1 đến 100 chia hết cho 4 là 100
Mà mỗi số chia hết cho 4 cách nhau 4 đơn vị
Nên số các số chia hết cho 4 là:
(100 – 4) : 4 + 1 = 25 (số).
Câu 9:
Tìm số ước của 120.
 Xem đáp án
Xem đáp án
Ta có: 120 = 23.3.5
Nên số ước của 120 là: (3 + 1).(1 + 1).(1 + 1) = 16 (ước).
Câu 10:
Cách giải bài toán đường thằg song song với trục hoành.
 Xem đáp án
Xem đáp án
Đường thẳng song song trục Ox có phương trình y = c khác 0 (c là hằng số) nên để đường thẳng có dạng y = ax + b song song với trục Ox thì a = 0 và b ≠ 0
Khi đó đường thẳng trở thành y = b và song song trục Ox.
Ví dụ: Cho đường thẳng d có phương trình (m - 2)x + (3m - 1)y = 6m – 2. Tìm các giá trị của tham số m để d song song với trục hoành.
Ta có: d: (m - 2)x + (3m - 1)y = 6m – 2
⇔ (3m - 1)y = -(m – 2)x + 6m - 2
Để d // Ox thì a = 0 và b ≠ 0, tức là:
Vậy m = 2 thì ta có phương trình d: y = 2 song song với trục hoành.
Câu 14:
Tìm giá trị của x để có nghĩa.
 Xem đáp án
Xem đáp án
có nghĩa khi x2 – x + 1 ≥ 0
⇔ (luôn đúng với mọi x)
Vậy với mọi giá trị của x thì có nghĩa.
Câu 15:
Đố: Biết rằng 12 + 22 + 32 + … + 102 = 385, đố em tính nhanh được tổng:
S = 22 + 42 + 62 + … + 202.
 Xem đáp án
Xem đáp án
S = 22 + 42 + 62 + ... + 202
S = (2.1)2 + (2.2)2 + (2.3)2 + ... + (2.10)2
S = 22.12 + 22.22 + 22.32 + … + 22.102
S = 22(12 + 22 + 32 + ... + 102)
S = 4.385
S = 1540.
Câu 16:
Giữa 2 số chẵn có tất cả 5 số lẻ. Tìm hiệu của 2 số đó?
 Xem đáp án
Xem đáp án
Hiệu của 2 số là:
5 . 2 + 1 = 11
Đáp số: 11
Câu 17:
Biết rằng 12 người lát xong nền của một ngôi nhà trong 8 ngày. Hỏi người ta muốn lát xong nền ngôi nhà đó trong 3 ngày thì cần bao nhiêu người? (Biết rằng mức làm của mỗi người như nhau).
 Xem đáp án
Xem đáp án
12 người thì lát xong nền của ngôi nhà trong 8 ngày, vậy để 1 người lát xong nền của 1 ngôi nhà cần số ngày là :
12 . 8 = 96 (ngày)
Nếu muốn lát xong nền của 11 ngôi nhà trong 3 ngày thì cần số người là:
96 : 3 = 32 (người)
Đáp số: 32 người.
Câu 18:
Biết rằng giá trị lớn nhất của hàm số y = |x4 − 38x2 + 120x + 4m| trên đoạn [0; 2] đạt giá trị nhỏ nhất. Khi đó giá trị của tham số m bằng?
 Xem đáp án
Xem đáp án
Xét x4 − 38x2 + 120x + 4m trên đoạn [0; 2] ta có:
f’(x) = 4x3 – 76x + 120 = 0
⇔
Suy ra:
Dấu ‘=” xảy ra khi .
Câu 19:
Cho hình tam giác vuông ABC, vuông tại A. Cạnh AB lớn hơn cạnh AC là 1m. Cạnh BC dài 500cm. Tính độ dài 2 cạnh AB và AC biết chu vi hình tam giác ABC là 12m.
 Xem đáp án
Xem đáp án
Đổi 12m = 1200cm; 1m = 100cm
Tổng độ dài AB và AC là:
1200 – 500 = 700 (cm)
Độ dài cạnh AC là:
(700 – 100) : 2 = 300 (cm)
Độ dài cạnh AB là:
300 + 100 = 400 (cm)
Câu 21:
Bỏ dấu ngoặc rồi tính các tổng sau:
a) (-28) + (-35) – 92 + (-82).
b) 15 – (-38) + (-55) – (+47).
 Xem đáp án
Xem đáp án
a) (-28) + (-35) – 92 + (-82)
= -28 – 35 – 92 – 82
= - (28 + 35 + 92 + 82)
= - [(28 + 82) + (35 + 92)]
= - (110 + 127)
= - 237.
b) 15 – (-38) + (-55) – (+47)
= 15 + 38 – 55 – 47
= 53 – 55 – 47
= - (55 – 53) – 47
= - 2 – 47
= - (2 + 47)
= - 49
Câu 22:
Bỏ dấu ngoặc rồi tính:
a) (29 + 37 + 13) + (10 - 37 - 13);
b) (79 + 32 - 35) - (69 + 12 - 75);
c) -(-125 + 63 + 57) - (10 - 83 - 37).
 Xem đáp án
Xem đáp án
a) (29 + 37 + 13) + (10 - 37 - 13)
= 29 + 37 + 13 + 10 - 37 - 13
= (37 – 37) + (13 – 13) + (29 + 10)
= 39
b) (79 + 32 - 35) - (69 + 12 - 75)
= 79 + 32 - 35 - 69 - 12 + 75
= (79 – 69) + (32 – 12) + (75 – 35)
= 10 + 20 + 40
= 70
c) -(-125 + 63 + 57) - (10 - 83 - 37)
= 125 - 63 - 57 - 10 + 83 + 37
= (125 – 10) + (83 + 37) + (- 63 – 57)
= 115 + 120 - 120
= 115.
Câu 24:
Viết tập hợp các số tự nhiên có hai chữ số , trong đó chữ số hàng chục nhỏ hơn chữ số hàng đơn vị là 4.
 Xem đáp án
Xem đáp án
Chữ số hàng chục và hàng đơn vị của các số cần lập được chọn từ các chữ số tự nhiên thuộc tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Trong tập hợp A, các cặp số cách nhau 4 đơn vị là: {0; 4}, {1; 5}, {2; 6}, {3; 7}, {4; 8}; {5; 9}.
Mà chữ số hàng chục khác 0
Nên ta lập được các số thỏa mãn yêu cầu bài toán là: 15; 26; 37; 48; 59.
Câu 25:
Bạn Nam đến nhà sách mua vở và mang theo 200 nghìn đồng, vừa đủ để mua 20 quyển vở loại A. Nhưng hiện tại nhà sách đang có chương trình khuyến mãi giảm 20% giá tiền mỗi quyển vở loại A. Hỏi với số tiền đang có, bạn Nam mua được tất cả bao nhiêu quyển vở loại A với giá khuyến mãi như trên?
 Xem đáp án
Xem đáp án
Số tiền mỗi quyển vở A là:
200000 : 20 = 10000 (đồng)
Số tiền sau khi được khuyến mãi là:
10000 - (10000 x 20 :100) = 8000 (đồng)
Vậy mua được:
200000 : 8000 = 25 (quyển).
Câu 26:
Bạn Việt mang 100000 đồng ra chợ mua hoa cúc và hoa hồng. Một bông hoa cúc có giá 3000 đồng, một bông hoa hồng có giá 6000 đồng. Gọi x và y lần lượt là số bông hoa cúc và số bông hoa hồng bạn Việt mua. Bất phương trình bậc nhất hai ẩn x, y để biểu diễn số tiền Việt mua hoa cúc và hoa hồng là?
 Xem đáp án
Xem đáp án
Theo bài ra ta có:
Một bông hoa cúc có giá 3000 đồng; x là số bông hoa cúc nên số tiền mua hoa cúc là 3000x
Tương tự: số tiền mua hoa hồng là 6000y
Mà Việt mang 100.000 đồng nên ta có: 3000x + 6000y ≤ 100.000
Hay 3x + 6y ≤ 100.
Vậy bất phương trình bậc nhất hai ẩn x, y để biểu diễn số tiền Việt mua hoa cúc và hoa hồng là 3x + 6y ≤ 100.
Câu 27:
Sau khi lấy 8kg gạo ở bao thứ nhất cho sang bao gạo thứ hai thì mỗi bao có 25kg gạo. Hỏi lúc đầu mỗi bao có bao nhiêu kg gạo?
 Xem đáp án
Xem đáp án
Lúc đầu bao thứ nhất có số kg gạo là:
8 + 25 = 32 (kg)
Lúc đầu bao thứ 2 có số kg gạo là:
25 - 8 = 17 (kg)
Đáp số: bao thứ nhất: 32 kg gạo; bao thứ hai: 17 kg gạo.
Câu 28:
 Xem đáp án
Xem đáp án
Vì a.b = (a, b).[a, b]
⇒ a.b = 630.18 = 11340
ƯCLN(a, b) = 18
⇒ a = 18.m; b = 18.n trong đó (m, n) = 1
Ta có: a.b = 11340
⇒ 18.m.18.n = 11340
⇒ m.n = 35
Mà (m, n) = 1
Ta có bảng:
|
m |
1 |
35 |
5 |
7 |
|
n |
35 |
1 |
7 |
5 |
|
a |
18 |
360 |
90 |
126 |
|
b |
360 |
18 |
126 |
90 |
Vậy (a;b) ∈ {(18;360), (360;18), (90;126), (126;90)}.
Câu 29:
Bệnh viện chia một đoàn gồm 60 bác sĩ và 96 y tá thành các đội đều nhau về số lượng bác sĩ và y tá. Số đội nhiều nhất có thể chia là bao nhiêu? Mỗi đội có bao nhiêu bác sĩ, bao nhiêu y tá?
 Xem đáp án
Xem đáp án
Gọi số đội được chia là a (a ∈ ℕ*)
Theo đề bài ta có:
60 ⋮ a, 96 ⋮ a nên a ∈ ƯCLN(60; 96)
Mà: 60 = 22.3.5
96 = 25.3
Suy ra: a ∈ ƯCLN(60; 96) = 22.3 = 12
Suy ra: a = 12
Vậy có 12 đội y tế
Mỗi đội có số bác sĩ là: 60 : 12 = 5 (bác sĩ)
Mỗi đội có số y tá là: 96 : 12 = 8 (y tá).
Câu 30:
Biến đổi biểu thức sina + 1 thành tích.
 Xem đáp án
Xem đáp án
Áp dụng công thức nhân đôi và chú ý: (đây là 2 góc phụ nhau)
.
Câu 31:
Bạn An muốn dùng tối đa 40000 đồng để mua viết, bạn ấy muốn mua ít nhất 2 cây viết loại thường và ít nhất 1 cây viết loại tốt. Viết loại tốt giá 10000 đồng 1 cây,
viết loại thường giá 5000 đồng/1 cây. Hỏi bạn An có tất cả bao nhiêu phương án lựa chọn?
A. 7.
B. 9.
C. 8.
D. 10
 Xem đáp án
Xem đáp án
Ta có: 40000 : 10000 = 4
Nên bạn An mua được nhiều nhất 4 loại viết loại tốt
Lại có: 40000 : 5000 = 8
Nên bạn An mua được nhiều nhất 8 loại viết thường
Ta gọi số lượng cây viết loại thường An mua là a (a ≥ 2); số lượng cây viết loại tốt An mua là b (b ≥ 1)
Ta có: 5000a + 10000b ≤ 40000
Hay 5a + 10b ≤ 40
Ta thấy a ≤ 6 để An có thể mua ít nhất 1 cây viết loại tốt
Để An có thể mua ít nhất 2 cây viết loại thường thì b ≤ 3
Vậy 2 ≤ a ≤ 6; 1 ≤ b ≤ 3
Suy ra: a ∈ {2;3;4;5;6}; b ∈ {1;2;3}
Nếu a = 6 thì b = 1 để 5000.6 + 10000.1 = 40000 (An đủ tiền mua)
Tương tự với các trường hợp còn lại, ta được
Nếu a = 5 thì b = 1
Nếu a = 4 thì b = 1 hoặc b = 2
Nếu a = 3 thì b = 1 hoặc b = 2
Nếu a = 2 thì b = 1 hoặc 2,3
Vậy An có tất cả 9 phương án lựa chọn.
Câu 32:
Bạn An về nghỉ hè ở quê một số ngày, trong đó có 10 ngày mưa. Biết rằng có 11 buổi sáng không mưa, có 9 buổi chiều không mưa và không bao giờ trời mưa cả sáng lẫn chiều. Hỏi bạn An về nghỉ ở quê trong bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Gọi x là số ngày An về nghỉ hè thì số ngày trời mưa vào buổi sáng là x - 11, số ngày trời mưa vào buổi chiều là x - 9
Suy ra số ngày mưa vào buổi chiều nhiều hơn số ngày mưa vào buổi sáng là:
(x - 9) - (x - 11) = 2 (ngày)
Số ngày trời mưa vào buổi sáng và buổi chiều có tổng là 10
Số ngày trời mưa vào buổi sáng là:
(10 - 2) : 2 = 4 (ngày)
Số ngày trời không mưa vào buổi sáng là 11 (theo đề bài)
Số ngày An về nghỉ hè là:
4 + 11 = 15 (ngày)
Đáp số: 15 ngày.
Câu 33:
 Xem đáp án
Xem đáp án
Do bạn bước vào phòng nên bạn đang đứng trên sàn.
Số cái chân đang đứng trên sàn nhà là: 2 cái chân.
Câu 34:
Bạn An cứ 4 ngày lại trực nhật một lần. Bạn Bình cứ 6 ngày lại trực nhật một lần. Bạn Cường cứ 8 ngày lại trực nhật một lần. Bà bạn cùng trực nhật lần đầu tiên vào hôm thứ Hai. Hỏi sau ít nhất bao nhiêu ngày ba bạn lại cùng trực nhật?
 Xem đáp án
Xem đáp án
Gọi số ngày ít nhất ba bạn lại cùng trực nhật là x (x ∈ ℕ*)
Theo bài ta có:
x chia hết cho 4
x chia hết cho 6
x chia hết cho 8
⇒ x = BCNN(4, 6, 8)
x là ít nhất
Ta có: 4 = 2²; 6 = 2 . 3; 8 = 2³
BCNN(4, 6, 8)= 2³ . 3 = 24
Vậy số ngày ít nhất ba bạn lại trực nhật cùng nhau là 24 ngày.
Câu 39:
Trong một giờ học tự chọn, lớp 4A có số học sinh học tiếng Anh và số học sinh Tin học. Hỏi số học sinh học Tin học và tiếng Anh bằng bao nhiêu phần tổng số học sinh cả lớp?
 Xem đáp án
Xem đáp án
Số học sinh Tin học và Tiếng anh bằng:
(số học sinh cả lớp).
Câu 40:
Một tòa nhà có chiều cao h (m). Khi tia nắng tạo với mặt đất một góc 55 độ thì bóng của tòa nhà trên mặt đất dài 15 m. Tính chiều cao h của tòa nhà.
 Xem đáp án
Xem đáp án
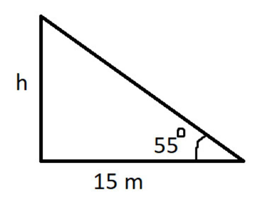
Áp dụng tỉ số lượng giác trong tam giác vuông, ta có:
Suy ra: h = 21,42 (m)
Vậy chiều cao tòa nhà là 21,42m.
Câu 43:
Một người bán 192kg gạo, trong đó số gạo nếp bằng 0,6 số gạo tẻ. Hỏi người đó bán được bao nhiêu tạ gạo mỗi loại?
 Xem đáp án
Xem đáp án
Đổi 0,6 = . Nên số gạo nếp bằng số gạo tẻ.
Tổng số phần bằng nhau là:
3 + 5 = 8 (phần)
Người đó bán được số gạo tẻ là:
192 : 8 . 5 = 120 (kg)
Người đó bán được số gạo nếp là:
192 - 120 = 72 (kg).
Câu 50:
Cho bản đồ tỷ lệ 1:25000, tính khoảng cách thực tế với 1cm; 2cm; 2,5cm.
 Xem đáp án
Xem đáp án
Khoảng cách thực tế với 1 cm là : 25000.1 = 25000 cm.
Khoảng cách thực tế với 2 cm là : 25000.2 = 50000 cm.
Khoảng cách thực tế với 2,5 cm là : 25000 . 2,5 = 62500 cm.
Câu 54:
Tính giá trị: 1 + 2,5 + 4 + 5,5 + 7 + ... + 100.
 Xem đáp án
Xem đáp án
Ta thấy: 2,5 – 1 = 1,5
4 – 2,5 = 1,5
7 – 5,5 = 1,5
Suy ra: Tổng trên là tổng các số hạng cách đều, số hạng sau hơn số hạng trước: 1,5 đơn vị.
Tổng trên có số số hạng là: (100 − 1) : 1,5 + 1 = 67.
Giá trị của tổng trên là: (100 + 1) . 67 : 2 = 3383,5.
Câu 55:
Tính D = 14 + 24 + 34 + … + n4.
 Xem đáp án
Xem đáp án
D = 14 + 24 + 34 + … + n4
Ta xét: u5 – (u – 1)5 = 5u4 – 10u3 + 10u2 – 5u + 1
Khi đó:
15 – 05 = 5.14 – 10.13 + 10.12 – 5.1 + 1
25 – 15 = 5.24 – 10.23 + 10.22 – 5.2 + 1
….
n5 – (n – 1)5 = 5n4 – 10n3 + 10n2 – 5n + 1
Cộng từng vế với vế ta được:
15 – 05 + 25 – 15 + … + n5 – (n – 1)5 = 5(14 + 24 + 34 + … + n4) – 10(13 + 23 + … + n3) + 10(12 + 22 + … + n2) – 5(1 + 2 + … + n) + n
⇔ n5 = 5.D – 10(13 + 23 + … + n3) + 10(12 + 22 + … + n2) – 5(1 + 2 + … + n) + n
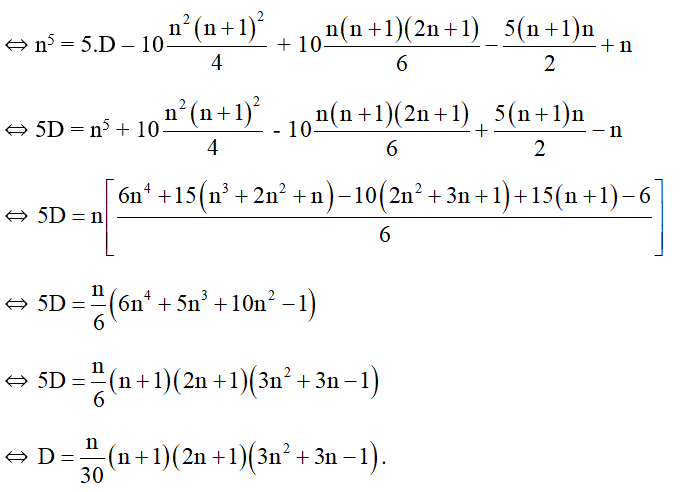
Câu 56:
Bỏ ngoặc rồi tính: 10 – [–12 – (–9 – 1)].
 Xem đáp án
Xem đáp án
10 – [–12 – (–9 – 1)]
= 10 – (–12 + 9 + 1)
= 10 + 12 – 9 – 1
= 22 – 9 – 1
= 12.
Câu 57:
Tìm thương và số dư (nếu có) của các phép chia sau:
a) 1092 : 91;
b) 2059 : 17.
 Xem đáp án
Xem đáp án
a) 1092 : 91 = 12 (dư 0).
b) 2059 : 17 = 121 (dư 2).
Câu 58:
Tính nhanh: 1 – 2 + 3 – 4 + 5 – 6 + ... + 19 – 20 + 21.
 Xem đáp án
Xem đáp án
1 – 2 + 3 – 4 + 5 – 6 + ... + 19 – 20 + 21
= (1 + 3 + 5 + … + 19 + 21) – (2 + 4 + 6 + … + 20)
Đặt A = (1 + 3 + 5 + … + 19 + 21) – (2 + 4 + 6 + … + 20)
Số số hạng của dãy thứ nhất là: (21 - 1 ) : 2 + 1 = 11 (số)
Tổng dãy thứ nhất là: (21 + 1) . 11 : 2 = 121
Số số hạng của dãy thứ hai là: (20 - 2 ) : 2 + 1 = 10 ( số )
Tổng dãy thứ hai là: (20 + 2) . 10 : 2 = 110
Vậy A = 121 - 110 = 11.
Vậy 1 – 2 + 3 – 4 + 5 – 6 + ... + 19 – 20 + 21 = 11.
Câu 59:
Tìm x biết 12 chia hết cho x và x > 4.
 Xem đáp án
Xem đáp án
12 chia hết cho x và x > 4.
Vì 12 chia hết cho x
Vậy x ∈ Ư (12) = {1; 2; 3; 4; 6; 12}.
Mà x > 4
Nên x ∈ {6; 12}.
Câu 60:
127 là bình phương của số nào?
 Xem đáp án
Xem đáp án
127 không phải là số chính phương vì số chính phương là các số có tận cùng là 0;1;4;5;6;9
Nên 127 không là bình phương của số nào.
Câu 62:
Tính tổng 1 – 3 + 32 – 33 + … + 399 – 3100.
 Xem đáp án
Xem đáp án
S = 1 – 3 + 32 – 33 + … + 399 – 3100
3S = 3 – 32 + 33 – 34 + … + 3100 – 3101
3S + S = (3 – 32 + 33 – 34 + … + 3100 – 3101) + (1 – 3 + 32 – 33 + … + 399 – 3100)
4S = 1 – 3100
S = .
Câu 65:
Tính B = 2 + 22 + 23 + … + 2n.
 Xem đáp án
Xem đáp án
B = 2 + 22 + 23 + … + 2n
2B = 22 + 23 + 24 + … + 2n+1
2B – B = (22 + 23 + 24 + … + 2n+1) – (2 + 22 + 23 + … + 2n)
B = 2n+1 – 2
B = 2(2n – 1)
Vậy B = 2(2n – 1).
Câu 68:
Hai người làm chung một công việc sau 4 giờ sẽ xong. Nếu một mình người thứ nhất thì sau 7 giờ sẽ xong. Hỏi nếu một mình người thứ hai làm thì sau bao lâu sẽ xong công việc ấy?
 Xem đáp án
Xem đáp án
Trong 1 giờ, người thứ nhất làm được công việc
Trong 1 giờ, cả 2 người làm được công việc
Trong 1 giờ, người thứ hai làm được là:
(công việc).
Thời gian người thứ hai làm một mình xong công việc là:
(giờ).
Câu 69:
Cho 3 lần cân thăng bằng 2 quả dứa bằng 2 quả cam, 1 quả dứa bằng 2 quả táo, 1 quả cam bằng 200g và 1 quả táo. Hỏi quả dứa cân nặng bao nhiêu gam?
 Xem đáp án
Xem đáp án
Ta có: 2 quả dứa = 2 quả cam (*)
1 quả dứa = 2 quả táo (1)
1 quả cam = 200g + 1 quả táo ⇒ 2 quả cam = 400g + 2 quả táo (2)
Lấy (1) – (2) ta được: 1 quả dứa – 2 quả cam = -400g
Hay 1 quả dứa = 2 quả cam – 400g
Thế (*) vào ta được: 1 quả dứa = 2 quả dứa – 400g
Suy ra: 1 quả dứa = 400g
Vậy quả dứa nặng 400g.
Câu 71:
Khẳng định nào sau đây đúng?
A. Hai vectơ cùng phương với 1 vectơ thứ ba thì cùng phương.
B. Hai vectơ cùng phương với 1 vectơ thứ ba khác thì cùng phương.
C. Vectơ không là vectơ không có giá.
D. Điều kiện cần và đủ để 2 vectơ bằng nhau là chúng có độ dài bằng nhau.
 Xem đáp án
Xem đáp án
Hai vectơ cùng phương với 1 vectơ thứ ba khác thì cùng phương.
Đáp án cần chọn là: B
Câu 72:
Xác định các hệ số a, b, c biết parabol có đồ thị hàm số y = ax2 + bx + c đi qua các điểm A(0; – 1), B(1; – 1), C(– 1; 1).
 Xem đáp án
Xem đáp án
Vì A ∈ (P), B ∈ (P), C ∈ (P) nên ta có hệ phương trình
Vậy a = 1; b = – 1; c = – 1.
Câu 74:
Cho a, b với ab ≥ 1. Chứng minh .
 Xem đáp án
Xem đáp án
Bất đẳng thức cần chứng minh tương đương: .
⇔ (a2 + b2 + 2)(ab + 1) ≥ 2(a2b2 + a2 + b2 + 1)
⇔ a3b + a2 + ab3 + b2 + 2ab + 2 ≥ 2a2b2 + 2a2 + 2b2 + 2
⇔ a3b + ab3 + 2ab ≥ 2a2b2 + a2 + b2
⇔ ab(a2 + b2 – 2ab) – (a2 + b2 – 2ab) ≥ 0
⇔ (a2 + b2 – 2ab)(ab – 1) ≥ 0
⇔ (a – b)2(ab – 1) ≥ 0
Vì ab ≥ 1 nên ab – 1 ≥ 0
Suy ra: (a – b)2(ab – 1) ≥ 0
Vậy điều này luôn đúng
Do đó ta có đpcm.
Vậy (dấu “=” xảy ra khi a = b hoặc ab = 1).
Câu 77:
Tính giá trị biểu thức: A = 2016 - 2015 + 2014 - 2013 + ... + 4 - 3 + 2 – 1.
 Xem đáp án
Xem đáp án
A = 2016 - 2015 + 2014 - 2013 + ... + 4 - 3 + 2 – 1
A = (2016 + 2014 + … + 4 + 2) – (2015 + 2013 + … + 3 + 1)
Xét B = 2016 + 2014 + … + 4 + 2
Số số hạng của dãy B là:
(2016 – 2) : 2 + 1 = 1008
Tổng dãy B là:
(2016 + 2) . 1008 : 2 = 1017072
Xét C = 2015 + 2013 + … + 3 + 1
Số số hạng của dãy C là:
(2015 – 1) : 2 + 1 = 1008
Tổng dãy B là:
(2015 + 1) . 1008 : 2 = 1016064
Vậy A = B – C = 1017072 – 1016064 = 1008.
Câu 78:
Tính nhanh: (-201).(-569) + (-201).469 + 301.100.
 Xem đáp án
Xem đáp án
(-201).(-569) + (-201).469 + 301.100
= (-201).[469 + (-569)] + 301.100
= (-201).(-100) + 301.100
= 201.100 + 301.100
= 100(301 + 201)
= 100.502
= 50200.
Câu 80:
 Xem đáp án
Xem đáp án
25(x + 5)2 – 9(x + 7)2
= [5.(x + 5)]2 – [3(x + 7)]2
= (5x + 25)2 – (3x + 21)2
= (5x + 25 + 3x + 21)(5x + 25 – 3x – 21)
= (8x + 46)(2x + 4)
= 2(4x + 23).2(x + 2)
= 4(4x + 23)(x + 2)
Câu 84:
Viết tập hợp số tự nhiên có 2 chữ số biết chữ số hàng chục nhỏ hơn chữ số hàng đơn vị, tổng 2 chữ số bằng 11.
 Xem đáp án
Xem đáp án
Gọi số có 2 chữ số là
Theo bài ra ta có: a < b và a + b = 11
Ta thấy: a > 1 vì nếu a = 1 thì b = 10 (vô lí vì là số có 2 chữ số)
Mà 11 = 2 + 9 = 3 + 8 = 4 + 7 = 5 + 6
Suy ra:
Vậy tập hợp các số tự nhiên cần tìm là {29;38;47;56}.
Câu 85:
Cho 2n - 1 là số nguyên tố. Chứng minh n cũng là số nguyên tố.
 Xem đáp án
Xem đáp án
Giả sử n là hợp số
Suy ra: n = p.q (p, q ∈ ℕ; p, q > 1)
Khi đó 2n – 1 = 2pq – 1 = (2p)q – 1
= (2p)q – 1q
= (2p – 1)[(2p)q-1 + (2p)q-2 + … + 1]
Vì p > 1 nên 2p – 1 > 1 và (2p)q-1 + (2p)q-2 + … + 1 > 1
Dẫn đến 2n – 1 là hợp số (trái với giả thiết 2n - 1 là số nguyên tố)
Vậy n là số nguyên tố.
Câu 92:
Cho các số nguyên dương x, y thỏa mãn (2x + 3y)2 + 5x + 5y + 1 là số chính phương. Chứng minh rằng x = y.
 Xem đáp án
Xem đáp án
Ta có: (2x + 3y)2 < (2x + 3y)2 + 5x + 5y + 1 < (2x + 3y + 2)2
Do đó để (2x + 3y)2 + 5x + 5y + 1 là số chính phương thì (2x + 3y)2 + 5x + 5y + 1 = (2x + 3y + 1)2
Khi đó: (2x + 3y)2 + 5x + 5y + 1 = (2x + 3y + 1)2
⇔ (2x + 3y)2 + 5x + 5y + 1 = [(2x + 3y) + 1)]2
⇔ (2x + 3y)2 + 5x + 5y + 1 = (2x + 3y)2 + 2(2x + 3y) + 1
⇔ (2x + 3y)2 + 5x + 5y + 1 = (2x + 3y)2 + 4x + 6y + 1
⇔ 5x + 5y = 4x + 6y
⇔ x = y
Vậy x = y.
Câu 94:
Nếu và x, y khác 0 thì tỉ số có giá trị bằng bao nhiêu?
 Xem đáp án
Xem đáp án
⇔ 2020(2x – y) = 2021x
⇔ 4040x – 2020y – 2021x = 0
⇔ 2019x – 2020y = 0
⇔ 2019x = 2020y
⇔
Vậy .
Câu 95:
Phân tích các đa thức sau thành nhân tử:
a) 2xy + 3z + 6y + xz;
b) a4 − 9a3 + a2a4 − 9a3 + a2 − 9a;
c) 3x2 + 5y − 3xy + (−5x);
d) x2 − (a + b)x + ab;
e) 4x2 − 4xy + y2 − 9t2;
g) x3 – 3x2y + 3xy2 – y3 – z3
h) x2 − y2 + 8x + 6y + 7.
 Xem đáp án
Xem đáp án
a) Cách 1.
Ta có 2xy + 3z + 6y + xz = (2xy + xz) + (3z + 6y)
= x(2y + z) + 3(z + 2y)
= (z + 2y)(x + 3).
Cách 2.
Ta có 2xy + 3z + 6y + xz = (2xy + 6y) + (3z + xz)
= 2y(x + 3) + z(3 + x)
= (z + 2y)(x + 3).
b) Biến đổi được a4 − 9a3 + a2 - 9a = (a – 9)a3 + a(a – 9) = (a – 9).a.(a2 + 1)
c) Biến đổi được 3x2 + 5y - 3xy + (-5x) = (x - y)(3x - 5).
d) Biến đổi được x2 - (a + b)x + ab = (x- a)(x - b).
e) Ta có 4x2 - 4xy + y2 – 9t2
= (2x − y)2 − (3t)2
= (2x - y - 3t )(2x - y + 31).
g) Ta có x3 − 3x2y + 3xy2 − y3 − z3
= (x − y)3 − z3
= (x - y - z)(x2 + y2 + z2- 2xy + xz - yz).
h) Ta có x2 − y2 + 8x + 6y + 7
= (x2 + 8x + 16) - (y2 - 6y + 9)
= (x + 4)2 − (y − 3)2
=(x – y + 7)(x + y + l).
Câu 96:
Cho x,y,z khác 0 thỏa mãn xy + yz + zx = 0 và x + y + z = -1. Hãy tính giá trị biểu thức .
 Xem đáp án
Xem đáp án
Ta có: x + y + z = -1 nên x + y = -(1 + z)
xy + yz + zx = 0
⇔ xy = -z(x + y) = z(z + 1)
Tương tự: xz = y (y + 1); yz = x .(x + 1)
.
Câu 97:
 Xem đáp án
Xem đáp án
B = 3 + 32 + … + 399
3B = 32 + 33 + … + 3100
3B – B = (32 + 33 + … + 3100) – (3 + 32 + … + 399)
2B = 3100 – 3
Mà không thể viết được dưới dạng n2
Nên B không phải số chính phương.
Câu 99:
Tìm x biết 3x + 3x+2 = 917 + 2712.
 Xem đáp án
Xem đáp án
3x + 3x+2 = 917 + 2712
⇔ 3x + 3x+2 = 917 + 2712
⇔ 3x + 3x.32 = (32)17 + (33)12
⇔ 3x(1 + 32) = 334 + 336
⇔ 3x(1 + 32) = 334(1 + 32)
⇔ 3x = 334
⇔ x = 34
Vậy x = 34.