- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 41)
-
12425 lượt thi
-
66 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Đồ thị hàm số có mấy đường tiệm cận ngang?
 Xem đáp án
Xem đáp án
Xét hàm số:
; nên đồ thị hàm số có 1 tiệm cận ngang là đường thẳng y = 0.
Vậy đồ thị hàm số có 1 tiệm cận ngang là đường thẳng y = 0.
Câu 2:
Chứng minh đồ thị hàm số không có tiệm cận ngang.
 Xem đáp án
Xem đáp án
Xét hàm số:
; nên đồ thị hàm số không có tiệm cận ngang
Vậy đồ thị hàm số không có tiệm cận ngang.
Câu 3:
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh Sxq của hình nón đó.
 Xem đáp án
Xem đáp án
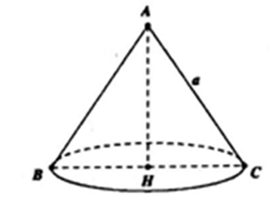
Khi quay tam giác ABC quanh đường cao AH ta được hình nón có bán kính đường tròn đáy là: R = BH = , đường sinh l = AB = a.
Diện tích xung quanh là:
Vậy diện tích xung quanh của hình nón là .
Câu 4:
Hình trụ có bán kính đáy bằng a, chu vi của thiết diện qua trục bằng 10a. Tính thể tích của khối trụ đã cho.
 Xem đáp án
Xem đáp án
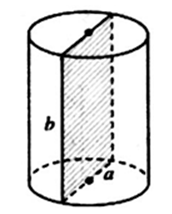
Thiết diện qua trục là 1 hình chữ nhật.
Giả sử chiều cao của hình trụ là b.
Theo đề ta có:
2(2a + b) =10a
Þ b = 3a
Thể tích khối trụ là:
Vậy thể tích của khối trụ đã cho là .
Câu 5:
Tìm m để phương trình m cosx + 1 = 0 có nghiệm.
 Xem đáp án
Xem đáp án
Để phương trình trên có nghiệm thì
• Trường hợp 1: m > 0
• Trường hợp 2: m < 0
Vậy m ≥ 1 hoặc m £ –1 thì phương trình có nghiệm.
Câu 6:
Giải phương trình: sin2x + 2sinx – 3 = 0.
 Xem đáp án
Xem đáp án
sin2x + 2sinx – 3 = 0
Û sin2x – sinx + 3sinx – 3 = 0
Û (sinx – 1)(sinx + 3) = 0
Vì –1 £ sinx £ 1 nên sinx + 3 ¹ 0
Do đó sinx – 1 = 0
Û sinx = 1
Vậy .
Câu 8:
 Xem đáp án
Xem đáp án
Để lấy ra ba quả cầu vừa khác màu vừa khác số ta phải thực hiện qua ba giai đoạn:
• Chọn một quả cầu đỏ.
• Chọn một quả cầu xanh.
• Chọn một quả cầu vàng.
• Chọn quả cầu đỏ có 5 cách chọn.
• Chọn quả cầu xanh có 5 cách chọn (trừ quả cầu được đánh số trùng với quả cầu đỏ).
• Chọn quả cầu vàng có 5 cách chọn (trừ hai quả cầu được đánh số trùng với quả cầu đỏ và quả cầu xanh).
Theo quy tắc nhân ta được 5. 5. 5 = 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.
Vậy có 125 cách lấy ra ba quả cầu vừa khác màu vừa khác số.
Câu 9:
Một hộp đựng 15 viên bi khác nhau gồm 4 bi đỏ, 5 bi trắng và 6 bi vàng. Tính số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu.
 Xem đáp án
Xem đáp án
• Trường hợp 1: chọn 4 bi đỏ hoặc trắng có:
(cách).
• Trường hợp 2: chọn 4 bi đỏ và vàng hoặc 4 bi vàng có:
(cách).
• Trường hợp 3: chọn 4 bi trắng và vàng có:
(cách)
Số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu là:
126 + 209 + 310 = 645 (cách)
Vậy có 645 cách.
Câu 10:
Tìm tập xác định của hàm số y = tanx.
 Xem đáp án
Xem đáp án
Ta có: .
Điều kiện xác định cosx ¹ 0
Vậy tập xác định của hàm số y = tanx là .
Câu 11:
Tìm tập xác định của hàm số .
 Xem đáp án
Xem đáp án
Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số là .
Câu 12:
Gọi S là tập hợp tất cả các số tự nhiên gồm 5 chữ số đôi một khác nhau được lập từ các chữ số 5, 6, 7, 8, 9. Tính tổng tất cả các số thuộc tập S.
 Xem đáp án
Xem đáp án
Số phần tử của tập S là 5! = 120 (số).
Mỗi số 5, 6, 7, 8, 9 có vai trò như nhau và xuất hiện ở hàng đơn vị số lần là:
4! = 24 (lần)
Tổng các chữ số xuất hiện ở hàng đơn vị là:
4! . (5 + 6 + 7 + 8 + 9) = 840 (chữ số)
Tương tự với các chữ số hàng chục, hàng tram, hàng nghìn và hàng chục nghìn.
Tổng tất cả các số thuộc tập S là:
840 . (104 + 103 + 102 + 10 + 1) = 9 333 240 (số)
Vậy tổng tất cả các số thuộc tập S là 9 333 240 số.
Câu 13:
 Xem đáp án
Xem đáp án
y = 2sinx – 3cos2x + 1 = 2sinx – 3(1 – 2sin2x) + 1 = 6sin2x + 2sinx – 2
Hàm số y đạt giá trị lớn nhất khi sinx = 1 khi và chỉ khi y = 6.
Vậy giá trị lớn nhất của y = 6.
Câu 14:
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện |z − i| = 1.
 Xem đáp án
Xem đáp án
Giả sử ta có số phức z = a + bi.
Thay vào |z − i| = 1 ta có:
|a + bi − i| = 1 ⇔ |a + (b − 1)i| = 1
⇔ a2 + (b − 1)2 = 1.
Vậy tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện |z − i| = 1 là đường tròn tâm I(0;1) và bán kính R = 1.
Câu 15:
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện z2 là một số ảo.
 Xem đáp án
Xem đáp án
Giả sử M(z) = (a;b)
Þ z = a + bi
Þ z2 = a2 – b2 + 2abi.
Khi đó z2 là một số ảo Û a2 – b2 = 0 Û a = ± b
Þ M(z) = (± b; b).
Vậy tập hợp các điểm biểu diễn số phức z trên mặt phẳng toạ độ thoả mãn điều kiện z2 là số ảo là đường thẳng y = x và y = − x (trừ gốc tọa độ O).
Câu 16:
Tìm giá trị nhỏ nhất của biểu thức sau: A = 5x2 – 6x + 9.
 Xem đáp án
Xem đáp án
Ta có A = 5x2 – 6x + 9
.
Vậy giá trị nhỏ nhất của biểu thức A là khi và chỉ khi .
Câu 17:
Giải phương trình: 4sin3x + 3cos3x – 3sinx – sin2xcosx = 0.
 Xem đáp án
Xem đáp án
• Trường hợp 1: cosx = 0 .
Khi đó sin2x = 1 ⇔ sinx = ± 1
Thay sinx = 1vào phương trình ta có: 4.1− 3.0 − 3.1 − 1.0 = 0 ⇔ 1 = 0 (vô lí)
không là nghiệm của phương trình.
• Trường hợp 2: cosx ≠ 0 .
Chia cả 2 vế của phương trình cho cos3x, ta được:
⇔ 4tan3x + 3 − 3tanx − 3tan3x − tan2x = 0
⇔ tan3x − tan2x − 3tanx + 3 = 0
⇔ tan2x(tanx − 1) − 3(tanx − 1) = 0
⇔ (tanx − 1)(tan2x − 3) = 0
Vậy hoặc .
Câu 20:
Cho hình vuông ABCD tâm O, cạnh a. Tính tích vô hướng .
 Xem đáp án
Xem đáp án
Ta có:
Vì ABCD là hình vuông nên:
Vậy .
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
 Xem đáp án
Xem đáp án
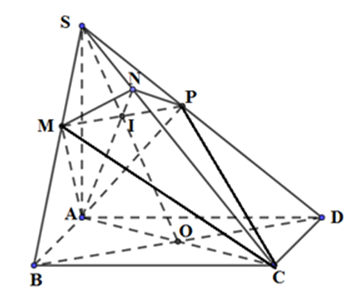
Gọi O là tâm của hình vuông ABCD nên O là trung điểm của AC
Ta có: CD ^ AD; CD ^ SA
Suy ra CD ^ (SAD) hay CD ^ AP
Lại có: SC ^ AP (do SC ⊥ (α)); CD ⊥ AP
Suy ra AP ⊥ (SCD) ⇒ AP ⊥ CP ⇒ ΔAPC vuông tại P
⇒ OA = OC = OP
Tương tự, ta có: ΔAMC vuông tại M
⇒ OA = OC = OM
Lại có: SC ⊥ AN (do SC ⊥ (α))
Khi đó ΔANC vuông tại N nên OA = OC = ON
⇒ OA = OC = OP = OM = ON
Þ O là tâm mặt cầu ngoại tiếp tứ diện CMNP
Bán kính của khối cầu là: .
Thể tích khối cầu ngoại tiếp tứ diện CMNP là:
.
Vậy thể tích khối cầu ngoại tiếp tứ diện CMNP là .
Câu 22:
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng . Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
 Xem đáp án
Xem đáp án
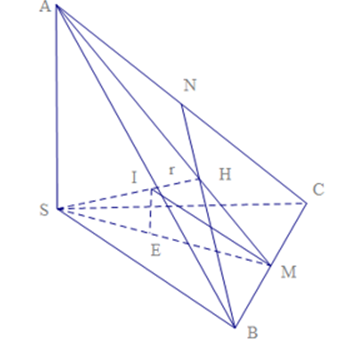
Áp dụng công thức (*) và tam giác đều cạnh x có diện tích
Từ giả thiết S.ABC đều có SA = SB = SC.
Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng nên ta có SA = SB = SC = a.
Suy ra và tam giác ABC đều cạnh có độ dài .
Do đó diện tích toàn phần của khối chóp S.ABC là:
Stp = SSAB + SSBC + SSCA + SABC
Thay vào (*) ta được:
Vậy r = .
Câu 23:
Cho (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm. Chứng minh 4 điểm A, B, M, O cùng thuộc 1 đường tròn.
 Xem đáp án
Xem đáp án
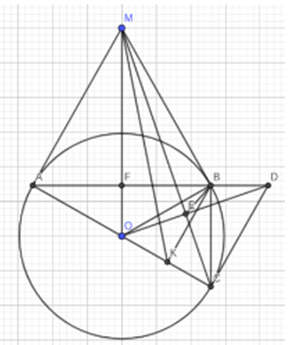
Vì MA, MB là tiếp tuyến của (O) nên ta có: MA ⊥ OA; MB ⊥ OB
Suy ra
Xét tứ giác AMBO có:
Do đó tứ giác AMBO nội tiếp
Vậy 4 điểm A, B, M, O cùng thuộc 1 đường tròn.
Câu 24:
Hàm số y = x3 − 3x + 2 đồng biến trên khoảng nào?
 Xem đáp án
Xem đáp án
TXĐ: D = R
Ta có: y′ = 3x2 – 3
Cho y′ ≥ 0
⇔ 3x2 − 3 ≥ 0
⇔ x ∈ (−∞; −1] ∪ [1; +∞).
Vậy hàm số đồng biến trên (−∞; −1) và (1; +∞).
Câu 25:
Hàm số y = x3 – 3x2 + 2 nghịch biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Ta có y’ =3x2 – 6x = 0
Bảng biến thiên:
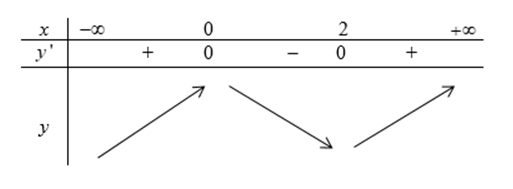
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng {0; 2}.
Câu 26:
Khi cộng hai số thập phân, Minh đã viết nhầm dấu phẩy của số hạnh thứ nhất sang bên phải một chữ số nên được tổng là 159,8. Tìm hai số đó biết tổng đúng là 47,3.
 Xem đáp án
Xem đáp án
Khi viết dấu phẩy sang bên phải mổ hàng nghĩa là số đó đã gấp lên 10 lần .
9 lần số hạng thứ nhất là:
159,8 − 47,3 = 112,5
Số hạng thứ nhất là:
112,5 : 9 = 12,5
Số hạng thứ hai là:
47,3 − 13,5 = 33,8
Vậy số hạng cần tìm là 33,8.
Câu 27:
Khi cộng hai số thập phân, một học sinh viết nhầm dấu phẩy của một số hạng bên phải một hàng, do đó được tổng là 49,1. Em hãy tìm hai số đã cho, biết rằng tổng đúng là 27,95.
 Xem đáp án
Xem đáp án
Khi viết nhầm như vậy thì số hạng đó tăng thêm 10 lần.
Vậy tổng sẽ tăng lên một lượng bằng 9 lần số hạng đó.
Lượng tăng là:
49,1 − 27,95 = 21,15
Vậy số hạng đó là:
21,15 : 9 = 2,35
Còn số hạng kia là:
27,95 − 2,35 = 25,6
Đáp số : 2,35 và 25,6
Câu 28:
Một đề trắc nghiệm có 50 câu hỏi gồm 20 câu mức độ nhận biết, 20 câu mức độ vận dụng và 10 câu mức độ vận dụng cao. Xác suất để bạn An làm hết 20 câu mức độ nhận biết là 0,9; 20 câu mức độ vận dụng là 0,8 và 10 câu mức độ vận dụng cao là 0,6. Xác suất để bạn An làm trọn vẹn 50 câu là?
 Xem đáp án
Xem đáp án
Gọi A là biến cố “bạn An làm trọn vẹn 50 câu”
• A1 là biến cố “bạn An làm hết 20 câu nhận biết”
• A2 là biến cố“ bạn An làm hết 20 câu vận dụng”
• A3 là biến cố “bạn An làm hết 10 câu vận dụng cao”
Khi đó: A = A1A2A3. Vì các biến cố A1; A2; A3 là độc lập nhau nên theo quy tắc nhân xác suất ta có:
P(A) = P(A1) . P(A2) . P(A3) = 0,9 . 0,8 . 0,6 = 0,432.
Vậy xác suất để bạn An làm trọn vẹn 50 câu là 0,432.
Câu 29:
Một thí sinh tham gia kì thi THPT Quốc gia. Trong bài thi môn Toán bạn đó làm được chắc chắn đúng 40 câu. Trong 10 câu còn lại chỉ có 3 câu bạn loại trừ được mỗi câu một đáp án chắc chắn sai. Do không còn đủ thời gian nên bạn bắt buộc phải khoanh bừa các câu còn lại. Hỏi xác suất bạn đó được 9 điểm là bao nhiêu?
 Xem đáp án
Xem đáp án
này phải trả lời đúng thêm 5 câu nữa.
Trong 10 câu còn lại chia làm 2 nhóm:
* Nhóm A là 3 câu đã loại trừ được một đáp án chắc chắn sai.
Nên xác suất chọn được phương án trả lời đúng là , xác suất chọn được phương án trả lời sai là .
* Nhóm B là 7 câu còn lại, xác suất chọn được phương án trả lời đúng là , xác suất chọn được phương án trả lời sai là .
Ta có các trường hợp sau:
• Trường hợp 1: Có 3 câu trả lời đúng thuộc nhóm A và 2 câu trả lời đúng thuộc nhóm B.
Xác xuất là
• Trường hợp 2: Có 2 câu trả lời đúng thuộc nhóm A và 3 câu trả lời đúng thuộc nhóm B.
Xác xuất là .
• Trường hợp 3: Có 1 câu trả lời đúng thuộc nhóm A và 4 câu trả lời đúng thuộc nhóm B.
Xác xuất là
• Trường hợp 4: Không có câu trả lời đúng nào thuộc nhóm A và 5 câu trả lời đúng thuộc nhóm B.
Xác xuất là .
Xác suất cần tìm là: .
Vậy xác suất bạn đó được 9 điểm là 0,079.
Câu 30:
Trong kỳ thi THPT Quốc Gia năm 2016 có môn thi bắt buộc là môn Tiếng Anh. Môn thi này thi dưới hình thức trắc nghiệm với 4 phương án trả lời A, B, C, D. Mỗi câu trả lời đúng được cộng 0,2 điểm và mỗi câu trả lời sai bị trừ đi 0,1 điểm. Bạn Hoa vì học rất kém môn Tiếng Anh nên chọn ngẫu nhiên cả 50 câu trả lời. Tính xác xuất để bạn Hoa đạt được 4 điểm môn Tiếng Anh trong kỳ thi trên.
 Xem đáp án
Xem đáp án
Gọi x là số câu trả lời đúng, suy ra 50 − x là số câu trả lời sai.
Ta có số điểm của Hoa là 0,2 . x − 0,1 . (50 − x) = 4 ⇔ x = 30 .
Do đó bạn Hoa trả lời đúng 30 câu và sai 20 câu.
Không gian mẫu là số phương án trả lời 50 câu hỏi mà bạn Hoa chọn ngẫu nhiên. Mỗi câu có 4 phương án trả lời nên có 450 khả năng.
Suy ra số phần tử của không gian mẫu là | Ω | = 450.
Gọi X là biến cố "Bạn Hoa trả lời đúng 30 câu và sai 20 câu".
Vì mỗi câu đúng có 1 phương án trả lời, mỗi câu sai có 3 phương án trả lời.
Vì vậy có . (3)20 khả năng thuận lợi cho biến cố X.
Suy ra số phần tử của biến cố X là | Ω X | = . (3)20.
Xác suất cần tính .
Vậy xác suất để bạn Hoa đạt được 4 điểm môn Tiếng Anh trong kỳ thi trên là .
Câu 32:
Cho đường thẳng (d): y = x – 1. Tính khoảng cách từ gốc tọa độ đến đường thẳng d.
 Xem đáp án
Xem đáp án
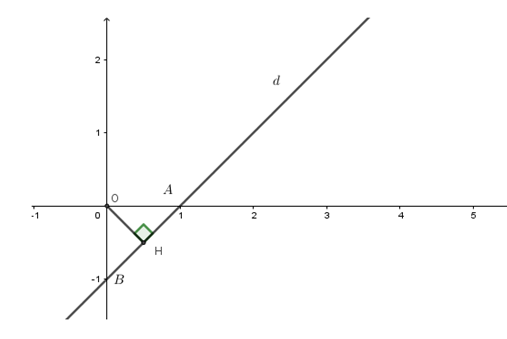
Ta có:
• d ∩ Ox tại A(1; 0) nên OA = 1
• d ∩ Oy tại B(0; −1) nên OB =1
Ta có: OA ⊥ OB
Gọi H là hình chiếu của O trên đường thẳng AB
Áp dụng hệ thức lượng trong tam giác vuông ta có:
Vậy khoảng cách từ gốc tọa độ đến đường thẳng d là .
Câu 33:
Trong mặt phẳng phức, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn .
 Xem đáp án
Xem đáp án
Gọi z = x + yi
Khi đó:
Ta có: ⇔ (x + yi)(x − yi) = 1 ⇔ x2 − (yi)2 = 1 ⇔ x2 + y2 = 1
Vậy tập hợp điểm biểu diễn số phức z là một đường tròn tâm O(0;0) và bán kính R = 1.
Câu 35:
Cho hàm số y = sinx – 3cosx. Tính vi phân của hàm số.
 Xem đáp án
Xem đáp án
Ta có: dy = y’dx = (sinx – 3cosx)’dx = (cosx + 3sinx)dx
Vậy vi phân của hàm số đã cho là (cosx + 3sinx)dx.
Câu 37:
Chú Nam gửi vào ngân hàng 10 triệu đồng với lãi đơn 5%/năm thì sau 5 năm số tiền chú Nam nhận được cả vốn lẫn lãi là bao nhiêu?
 Xem đáp án
Xem đáp án
Số tiền cả gốc lẫn lãi chú Nam nhận được sau 5 năm là:
S5 = 10.(1 + 5.0,05) = 12,5 (triệu đồng).
Đáp số: 12,5 triệu đồng.
Câu 38:
Chị Hằng gửi ngân hàng 3 350 000 đồng, theo phương thức lãi đơn, với lãi suất 0,4% trên nửa năm. Hỏi ít nhất bao lâu chị rút được cả vốn lẫn lãi là 4 020 000 đồng?
 Xem đáp án
Xem đáp án
Gọi n là số chu kỳ gửi ngân hàng, áp dụng công thức lãi đơn ta có:
4 020 000 = 3 350 000(1 + n.0,04)
4 020 000 = 3 350 000 + 134 000.n
670 000 = 134 000.n
Suy ra, n = 5 (chu kỳ)
Mà nửa năm = 6 tháng
Thời gian ít nhất chị rút được cả vốn lẫn lãi là 4 020 000 đồng là:
5.6 = 30 (tháng)
Đáp số: 30 tháng
Câu 39:
Cho hàm số y = x3 + 3x2 + 1 có đồ thị (C). Gọi d là tiếp tuyến của đồ thị hàm số tại điểm A(1;5) và B là giao điểm thứ hai của d với (C). Tính diện tích tam giác OAB?
 Xem đáp án
Xem đáp án
Hàm số y = x3 + 3x2 + 1
Xét đạo hàm: y′ = 3x2 + 6x
⇒ y′(1) = 9
Phương trình tiếp tuyến của đồ thị hàm số tại điểm A(1;5) là:
y = 9(x − 1) + 5 = 9x – 4 ⇔ 9x – y – 4 = 0 (d) hay y = 9x – 4
Xét phương trình hoành độ giao điểm:
x3 + 3x2 + 1 = 9x – 4
Û x3 + 3x2 – 9x + 5 = 0
Do đó giao điểm thứ hai của d với (C) là B(–5; –49).
Vậy .
Câu 40:
Tìm m để có tập xác định D = R.
 Xem đáp án
Xem đáp án
Trường hợp 1: m + 1 ³ 0 Û m ³ −1
Hàm số xác định trên R Û 3x2 – 2x + m > 0,
Trường hợp 2: m + 1 < 0 Û m < −1
Hàm số xác định trên R Û 3x2 – 2x + m > 0,
Điều này không xảy ra vì hàm số y = Û 3x2 – 2x + m có a = 3 > 0 nên không thể luôn âm trên R.
Câu 41:
Chứng minh đồ thị hàm số y = 2x2 đi qua điểm A(–1; 2)
 Xem đáp án
Xem đáp án
Thay x = −1 vào y = 2x2, ta được:
y = 2.(−1)2 = 2
Þ Đồ thị hàm số y = 2x2 đi qua điểm (−1;2).
Vậy đồ thị hàm số y = 2x2 đi qua điểm (−1;2).
Câu 42:
Điểm N(1; 4) có thuộc đồ thị hàm số y = –2x không?
 Xem đáp án
Xem đáp án
Thay toạ độ điểm N(1; 4) vào đồ thị hàm số y = –2x ta có:
y = –2x = –2.1 = –2 ¹ 4
Vậy điểm N(1; 4) không thuộc đồ thị hàm số y = –2x.
Câu 44:
Gọi A, B là giao điểm của đồ thị hàm số và đường thẳng y = −x − 1. Tính AB.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
⇔ 2x + 1 = −x2 − 2x – 1
⇔ x2 + 4x + 2 = 0
Gọi x1, x2 là 2 nghiệm của phương trình trên.
Theo Vi-ét, ta có: x1 + x2 = −4 và x1x2 = 2
Tọa độ các điểm A(x1; y1), B(x2; y2)
Độ dài đoạn AB là:
.
Vậy AB = 4.
Câu 45:
Biết tổng các hệ của khai triển (x² + 1)n bằng 1024. Hãy tìm hệ số của x¹² trong khai triển trên.
 Xem đáp án
Xem đáp án
.
Do tổng các hệ của khai triển bằng 1024.
Þ (1 + 1)n = 1024 Û 2n = 210 Û n = 10
.
Hệ số của x12 tương ứng với 2k = 12 Û k = 6.
Hệ số của x12 là: .
Vậy hệ số của x12 là .
Câu 46:
Tìm hệ số của x12 trong khai triển nhị thức Niu-tơn (2x − x2)10.
 Xem đáp án
Xem đáp án
Ta có:
Hệ số của x12 tương ứng với 10 + k = 12 Û k = 2
Do đó hệ số của x12 là .
Câu 47:
Với sự phát triển của khoa học kỹ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng. Chi phí sản để sản xuất ra một chiếc xe lăn là 2 500 000 đồng. Gía bán ra mỗi chiếc là 3 000 000 đồng. Viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn ban đầu và chi phí sản xuất) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.
 Xem đáp án
Xem đáp án
Tổng chi phí vốn cố định và vốn sản xuất ra x chiếc xe lăn (đơn vị triệu đồng): y = 500 + 2,5x.
Hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn là: y = 3x.
Vậy hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn ban đầu và chi phí sản xuất) là y = 500 + 2,5x và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn là y = 3x.
Câu 48:
Giải phương trình: .
 Xem đáp án
Xem đáp án
Điều kiện: x ≥ 6
Dễ thấy
Þ x – 9 = 0
Û x = 9 (TM)
Vậy x = 9.
Câu 49:
Giải phương trình: .
 Xem đáp án
Xem đáp án
Điều kiện: x2 + 2x + 3 ≥ 0
Đặt ; b = 2x +1, phương trình trở thành:
a2 + 2b = ab + 4
⇔ a2 − 4− ab + 2b = 0
⇔ (a − 2)(a + 2) − b(a − 2) = 0
⇔ (a − 2)(a – b + 2) = 0
.
• Với a = 2
Û x2 + 2x – 1 = 0
• Với a – b = −2
⇔ x2 + 2x+ 3 = 4x2 − 4x + 1
⇔3x2 − 6x − 2 =0
Vậy tập hợp giá trị x thỏa mãn là: .
Câu 50:
Bác Kim gửi một số tiền vào ngân hàng với lãi suất là 7% và kì hạn là một năm. Sau một năm bác Kim tới ngân hàng rút cả vốn lẫn lãi được 128 400 000 đồng. Hỏi lúc đầu bác Kim gửi vào ngân hàng bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Gọi số tiền bác Kim gửi vào ngân hàng là x (đồng) (![]() )
)
Số tiền lãi sau một năm là:
x.7% = 0,07x (đồng)
Sau một năm bác tới ngân hàng rút là 128 400 000 nên ta có phương trình là:
x + 0,07x = 128 400 000
⇔1,07x = 128 400 000
⇔ x = 120 000 000 (TM)
Đáp số: 120 000 000 đồng.
Câu 51:
Bà Mai vay ngân hàng 200 triệu trong thời gian 2 năm để mở một cửa hàng chuyên sản xuất và bán quà lưu niệm. Theo hợp đồng vay vốn, lãi suất vay trong một năm là 10%. Sau 1 năm, tiền lãi của năm đầu sẽ được cộng vào vốn của năm sau. Hỏi sau 2 năm, Bà Mai phải trả ngân hàng bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Số tiền lãi bà Mai phải trả năm đầu là:
200. 10 : 100 = 20 (triệu đồng)
Số tiền bà phải trả cả gốc lẫn lãi năm đầu là:
200 + 20 = 220 (triệu đồng)
Số tiền lãi năm 2 bà Mai phải trả là:
220. 10 : 100 = 22 (triệu đồng)
Số tiền bà Mai phải trả trong 2 năm là:
220 + 22 = 242 (triệu đồng)
Đáp số: 242 triệu đồng.
Câu 52:
Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang là?
 Xem đáp án
Xem đáp án
Vì có 10 ghế nên bạn thứ nhất có 10 cách xếp.
• Bạn thứ hai có 9 cách xếp.
• Bạn thứ ba có 8 cách xếp.
• Bạn thứ tư có 7 cách xếp.
• Bạn thứ năm có 6 cách xếp.
• Bạn thứ sáu có 5 cách xếp.
Như vậy có: 10 . 9 . 8 . 7 . 6 . 5 = (cách xếp).
Vậy có cách xếp.
Câu 53:
Khai triển đa thức P(x) = (2x – 1)1000 ta được P(x) = a1000 x1000 + a999 x999 + … + a1x + a0.
 Xem đáp án
Xem đáp án
Ta có
P(x) = a1000 x1000 + a999 x999 + … + a1x + a0
Cho x = 1 ta được
P(1) = a1000 + a999 + … + a1 + a0
Mặt khác
P(x) = (2x – 1)1000
Do đó P(1) = (2 . 1 – 1)1000 = 1
Từ đó suy ra P(1) = a1000 + a999 + … + a1 + a0 = 1
Do đó a1000 + a999 + … + a1 = 1 – a0
Mà là số hàng không chứa x trong khai triển P(x) = (2x – 1)1000
Nên .
Vậy a1000 + a999 + … + a1 = 0.
Câu 54:
Tìm giá trị thực của tham số m để đường thẳng d: y = (2m − 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 1.
 Xem đáp án
Xem đáp án
Tập xác định: D = R
Ta có: y′ = 3x2 − 6x = 0
Do đó A(0;1) và B(2; −3) là hai điểm cực trị của đồ thị hàm số đã cho.
Phương trình đường thẳng đi qua hai điểm cực trị là:
⇔ −2x = y – 1 ⇔ y = −2x + 1 (d′)
Vì d ⊥ d′ ⇒ (2m − 1).(−2) = −1
Vậy .
Câu 55:
Tìm m để đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1.
 Xem đáp án
Xem đáp án
Vì đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1 nên ta có:
Vậy với m = 3 thì đường thẳng y = 2m – 1x + 3 song song với đường thẳng y = 5x – 1.
Câu 56:
Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số cắt đường thẳng (d’): y = 2x + 1 tại điểm có hoành độ bằng –2.
 Xem đáp án
Xem đáp án
Để đường thẳng (d) cắt đường thẳng (d’) thì 2k – 1 ¹ 2 hay
Thay x = –2 vào hàm số y = 2x + 1
Û y = 2. (–2) + 1 = –3
Gọi A(–2; –3)
Do đường thẳng (d) và (d’) cắt nhau tại A nên:
–3 = (2k – 1)( –2) + 3 – k
Û –4k + 2 + 3 – k + 3 = 0
Û –5k + 8 = 0
(TMĐK)
Vậy giá trị k thỏa mãn là .
Câu 57:
Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m):y = 0,5x – 3.
 Xem đáp án
Xem đáp án
Để đường thẳng (d) // (m) thì:
Vậy giá trị k thỏa mãn là .
Câu 58:
Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các chữ số đó bằng 7?
 Xem đáp án
Xem đáp án
Gọi số cần tì có dạng
• Trường hợp 1: Trong 4 chữ số a, b, c, d có 3 chữ số bằng 0
Þ b = c = d = 0, a = 7
Do đó có 1 số thỏa mãn.
• Trường hợp 2: Trong 4 chữ số a, b, c, d có 2 chữ số bằng 0.
Chọn vị trí cho 2 chữ số 0 có (cách).
Tổng hai chữ số còn lại là 7, ta có:
7 = 6 + 1 = 5 + 2 = 4 + 3 = 3 + 4 = 2 + 5 = 1 + 6
Nên có 6 cách chọn 2 chữ số còn lại.
Do đó trường hợp này có 18 số.
• Trường hợp 3: Trong 4 chữ số a, b, c, d có 1 chữ số bằng 0.
Chọn vị trí cho 1 chữ số 0 có (cách).
Tổng ba chữ số còn lại là 7, ta có
7 = 1 + 1 + 5 = 1 + 2 + 4 = 1 + 3 + 3 = 2 + 2 + 3
Với bộ số (1; 2; 4) có 3! = 6 cách chon 3 chữ số còn lại.
Với 3 bộ số còn lại có cách chọn 3 chữ số còn lại.
Do đó trường hợp này có 3 . (6 + 3 . 3) = 45 (số).
• Trường hợp 4: Trong 4 chữ số a, b, c, d không có chữ số bằng 0
Ta có:
+) Với bộ số(1; 1; 1; 4) có cách chọn 4 chữ số a, b, c, d.
+) Với bộ số(1; 1; 2; 3) có cách chọn 4 chữ số a, b, c, d.
Với bộ số(1; 2; 2; 2) có cách chọn 4 chữ số a, b, c, d.
Do đó trường hợp này có 4 + 12 + 4 = 20 số thỏa mãn.
Vậy có tất cả: 1 + 18 + 45 + 20 = 84 số.
Câu 59:
Một cửa hàng sách hạ giá 10% giá sách nhân ngày Quốc tế thiếu nhi 1 – 6. Tuy vậy, cửa hàng vẫn còn lãi 8%. Hỏi ngày thường thì cửa hàng được lãi bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Do hạ giá 10% nên giá bán mới bằng 90% giá ngày thường
Coi giá vốn là 100% thì giá bán mới bằng 108% giá vốn
Như vậy giá vốn bằng giá ngày thường
Giá ngày thường so với giá vốn là:
Ngày thường thì cửa hàng được lãi là:
120% – 100% = 20%
Đáp số: 20%
Câu 60:
Sau khi giảm giá 20% thì giá của một quyển sách là 9 600 đồng. Hỏi lúc đầu gái của quyển sách là bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Coi giá ban đầu là 100% thì giá sách sau khi giảm đi 20% là:
100% – 20% = 80%
Vậy lúc đầu giá của cuốn sách đó là:
9600 : 80 × 100 = 12 000 (đồng)
Đáp số: 12000 đồng
Câu 61:
 Xem đáp án
Xem đáp án
Điều kiện xác định x2 + 5x – 6 > 0
Þ (–¥; –6) È (1; +¥)
Câu 62:
Tìm tập xác định D của hàm số y = log2(x3 − 8)1000.
 Xem đáp án
Xem đáp án
Điều kiện (x3 − 8)1000 > 0 ⇔ x ≠ 2
Tập xác định D = R∖{2}
Câu 64:
Xếp 4 bạn nam và 2 bạn nữ thành một hàng ngang. Xác xuất để 2 bạn nữ không ngồi cạnh nhau là?
 Xem đáp án
Xem đáp án
Xếp 4 bạn nam và 2 bạn nữ thành 1 hàng ngang
Þ n(W) = 6! = 720.
Gọi A là biến cố: “ 2 bạn nữ không ngồi cạnh nhau”.
Xếp 4 bạn nam có 4! cách, khi đó sẽ tạo ra 5khaongr trống giữa 4 bạn nam, xếp 2 bạn nữ vào 2 trong 5 khoảng trống nay có ![]() cách.
cách.
.
Vậy .
Câu 65:
Xếp 5 nam và 2 nữ vào một bàn dài gồm 7 chỗ ngồi. Tính xác suất để 2 nữ không ngồi cạnh nhau.
 Xem đáp án
Xem đáp án
Xếp 7 bạn vào 7 vị trí có n(Ω) = 7! = 5 040 (cách)
Gọi A là biến cố 2 bạn nữ ngồi cạnh nhau.
Chọn 2 bạn từ 2 bạn nữ có 1 cách
Coi 2 bạn nữ đó là một ẩn, xếp 6 vào 6 vị trí có 6! cách
Xếp 2 bạn nữ đảo chỗ cho nhau có 2 cách
Do đó số cách xếp 2 bạn ngồi cạnh nhau là:
n(A) = 1.6!.2 = 1440 (cách)
Xác suất xếp 2 bạn nữ ngồi cạnh nhau là:
.
Xác suất xếp 2 bạn nữ không ngồi cạnh nhau là: .
Câu 66:
Trong mặt phẳng Oxy, cho điểm B (−3; 6). Tìm tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay (−90º).
 Xem đáp án
Xem đáp án
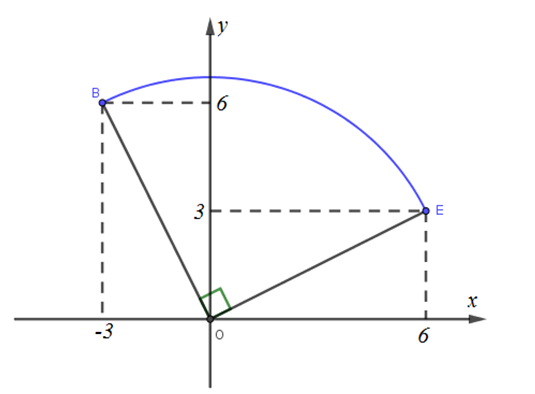
Tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay (−90º).
Khi đó, tọa độ cần tìm là E(3; 6).