- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 58)
-
12365 lượt thi
-
51 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
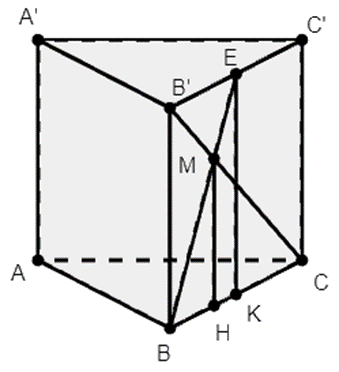
Kẻ MH ⊥ BC, EK ⊥ BC.
Ta có: (g.g)
\( \Rightarrow \frac{{ME}}{{MB}} = \frac{{B'E}}{{CB}} = \frac{1}{2}\).
(g.g)
\( \Rightarrow \frac{{MH}}{{KE}} = \frac{{BM}}{{BE}} = \frac{2}{3}\)
\( \Rightarrow MH = \frac{2}{3}EK = \frac{2}{3}.6a = 4a\)
\(V = \frac{1}{3}MH.{S_{\Delta ABC}} = \frac{1}{3}.4a.\left( {\frac{1}{2}.3a.3a} \right) = 6{a^3}\).
Câu 2:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
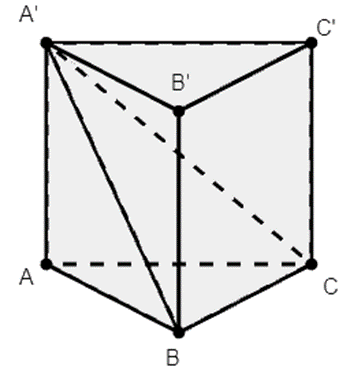
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot \left( {A'BA} \right) \Rightarrow \widehat {A'BA} = 30^\circ \)
Khi đó \(AA' = AB.\tan 30^\circ = \frac{{2a}}{{\sqrt 3 }}\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \frac{{4{a^2}}}{2}.\frac{{2a}}{{\sqrt 3 }} = \frac{{4{a^3}\sqrt 3 }}{3}\)
Câu 3:
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và \(\widehat {ABC} = 120^\circ \). Các cạnh AA', A'B, A'D cùng tạo với đáy một góc 60°. Tính theo a thể tích V của khối lăng trụ đã cho.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
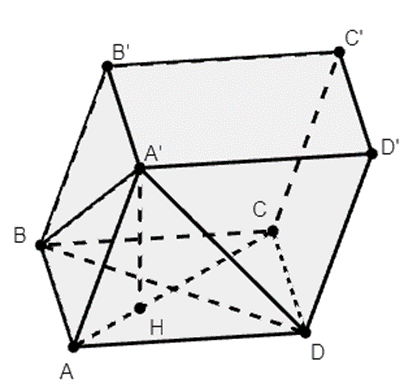
Ta có: \(\widehat {ABC} = 120^\circ \Rightarrow \widehat {BAD} = 60^\circ \) suy ra tam giác ABD là tam giác đều cạnh a.
Khi đó A’.ABD là chóp đều cạnh đáy bằng a.
Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tam tam giác ABD.
Ta có: \(A'H = HA.\tan 60^\circ = \frac{{a\sqrt 3 }}{3}.\sqrt 3 = a\)
\( \Rightarrow {V_{A'.ABD}} = \frac{1}{3}A'H.{S_{ABC}} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Do đó \({V_{ABCD.A'B'C'D'}} = 3.{V_{A'.ABCD}} = 6.{V_{A'.ABD}} = \frac{{{a^3}\sqrt 3 }}{2}\).
Câu 4:
Quãng đường AB gồm một đoạn lên dốc dài 4 km và một đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
 Xem đáp án
Xem đáp án
Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4 km và đoạn xuống dốc dài 5 km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là \(\frac{4}{x}\) (h), thời gian xuống dốc là: \(\frac{5}{y}\) (h)
Theo đầu bài thời gian đi A đến B là 40 phút \( = \frac{2}{3}\) (h) nên:
\(\frac{4}{x} + \frac{5}{y} = \frac{2}{3}\) (1)
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là \(\frac{5}{x}\) (h), thời gian xuống dốc là: \(\frac{4}{y}\) (h)
Theo đầu bài thời gian đi A đến B là 41 phút \( = \frac{{41}}{{60}}\) (h) nên:
\(\frac{5}{x} + \frac{4}{y} = \frac{{41}}{{60}}\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}\frac{4}{x} + \frac{5}{y} = \frac{2}{3}\\\frac{5}{x} + \frac{4}{y} = \frac{{41}}{{60}}\end{array} \right.\)
Đăth \(X = \frac{1}{x};Y = \frac{1}{y}\) khi đó hệ phương trình trên trở thành:
\(\left\{ \begin{array}{l}4X + 5Y = \frac{2}{3}\\5X + 4Y = \frac{{41}}{{60}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}X = \frac{1}{{12}}\\Y = \frac{1}{{15}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 12\\y = 15\end{array} \right.\) (TMĐK)
Vậy tốc độ lúc lên dốc là 12 km/h, vận tốc lúc xuông dốc là 15 km/h.
Câu 5:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
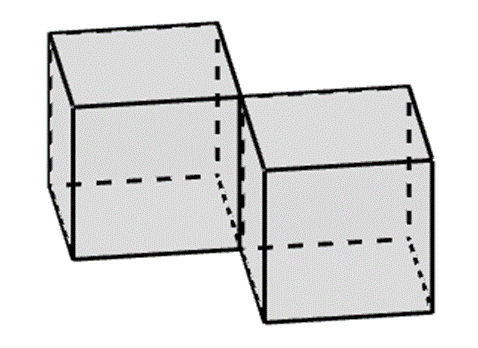
Lắp ghép 2 khối hộp chưa chắc được 1 khối đa diện lồi.
Câu 6:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Không thể tồn tại khối chóp tứ giác đều là khối đa diện đều.
Câu 7:
Tìm một số tự nhiên có hai chữ số,biết rằng nếu viết thêm chữ số 6 vào bên trái số đó ta được một số lớn gấp 13 lần số đã cho.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi số phải tìm là: \(\overline {ab} \). Viết thêm chữ số 9 vào bên trai ta được số \(\overline {9ab} \).
Theo đề bài, ta có:
\(6\overline {ab} = \overline {ab} \times 13\)
\(600 + \overline {ab} = \overline {ab} \times 13\)
\(600 = \overline {ab} \times 13 - \overline {ab} \)
\(600 = \overline {ab} \left( {13 - 1} \right)\)
\(600 = 12 \times \overline {ab} \)
\(\overline {ab} = 600:12 = 50\)
Vậy số cần tìm là 50.
Câu 8:
Cho phương trình (m + 1).16x − 2( 2m − 3) .4x + 6m + 5 = 0 với m là tham số thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng (a; b). Tính P = a.b.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đặt t = 4x > 0
Phương trình trở thành:
(m + 1).t2 – 2(2m – 3)t + 6m + 5 = 0 (*)
Phương trình đã cho có hai nghiệm thỏa mãn x1 < 0 < x2
\( \Rightarrow 0 < {4^{{x_1}}} < {4^0} < {4^{{x_2}}}\)
Suy ra: 0 < t1 < 1 < t2
YCBT trở thành:
Phương trình (*) có hai nghiệm t1; t2 thỏa mãn
0 < t1 < 1 < t2 \( \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 0\\\left( {m + 1} \right)f(1) < 0\\\left( {m + 1} \right)f(0) > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 0\\\left( {m + 1} \right)\left( {3m + 12} \right) < 0\\\left( {m + 1} \right)\left( {6m + 5} \right) > 0\end{array} \right.\)
⇔ −4 < m < −1
\( \Rightarrow \left\{ \begin{array}{l}a = - 4\\b = - 1\end{array} \right. \Rightarrow P = 4\)
Vậy P = 4.
Câu 9:
Tìm tất cả các giá trị thực của tham số m để phương trình mx – m = 0 vô nghiệm.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: mx – m = 0 vô nghiệm
\( \Leftrightarrow \left\{ \begin{array}{l}m = 0\\m \ne 0\end{array} \right. \Leftrightarrow m \in \emptyset \)
Vậy không tồn tại m để phương trình đã cho vô nghiệm hay m ∈ ∅.
Câu 10:
Tìm tất cả các giá trị thực của tham số m để phương trình (m2 – 4)x = 3m + 6 vô nghiệm.
 Xem đáp án
Xem đáp án
Ta có: (m2 – 4)x = 3m + 6 ⇔ (m2 – 4)x – 3m – 6 = 0 vô nghiệm
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4 = 0\\ - 3m - 6 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\\m \ne - 2\end{array} \right. \Leftrightarrow m = 2\)
Vậy với m = 2 thỏa mãn yêu cầu bài toán.
Câu 11:
Cho một khối chóp có thể tích bằng V. Khi giảm chiều cao của hình chóp xuống 2 lần và tăng diện tích đáy lên 4 lần thì thể tích khối chóp lúc đó bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi V,h,S lần lượt là thể tích, chiều cao, và diện tích đáy của hình chóp ban đầu.
V′, h′, S′ lần lượt là thể tích, chiều cao, và diện tích đáy của hình chóp khi đã thay đổi kích thước.
Theo giả thiết: \(h' = \frac{h}{2}\), S’ = 4S.
Ta có: \(V' = \frac{1}{3}.S'.h' = \frac{1}{3}.4S.\frac{h}{2} = 2.\left( {\frac{1}{3}.S.h} \right) = 2V\).
Câu 12:
Phương trình \(2{\sin ^2}x + \sqrt 3 \sin 2x = 3\) có nghiệm là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(2{\sin ^2}x + \sqrt 3 \sin 2x = 3\)
\( \Leftrightarrow 2{\sin ^2}x - 1 + \sqrt 3 \sin 2x = 2\)
\( \Leftrightarrow - \left( {1 - 2{{\sin }^2}x} \right) + \sqrt 3 \sin 2x = 2\)
\( \Leftrightarrow - \cos 2x + \sqrt 3 \sin 2x = 2\)
\( \Leftrightarrow \sqrt 3 \sin 2x - \cos 2x = 2\)
\( \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin 2x - \frac{1}{2}\cos 2x = 1\)
\( \Leftrightarrow \cos \frac{\pi }{6}.\sin 2x - \sin \frac{\pi }{6}.\cos 2x = 1\)
\( \Leftrightarrow \sin \left( {2x - \frac{\pi }{6}} \right) = 1\)
\( \Leftrightarrow 2x - \frac{\pi }{6} = \frac{\pi }{2} + k2\pi \), k ∈ ℤ
\( \Leftrightarrow x = \frac{\pi }{3} + k\pi \), k ∈ ℤ.
Vậy phương trình có họ nghiệm là: \(x = \frac{\pi }{3} + k\pi \), k ∈ ℤ.
Câu 13:
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét hình lăng trụ như hình vẽ:
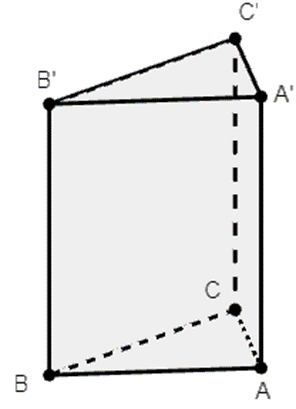
Tam giác ABC đều nên có diện tích \({S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\).
Chiều cao của khối lăng trụ là AA’ = 2a suy ra thể tích của khối lăng trụ tam giác đều ABC.A’B’C’ là \(V = AA'.{S_{ABC}} = \frac{{{a^3}\sqrt 3 }}{2}\) (đvtt)
Câu 14:
Thể tích của khối lăng trụ đứng tam giác đều có cạnh bên bằng a, cạnh đáy bằng 2a bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thể tích của khối lăng trụ đứng tam giác đều có cạnh bên bằng a, cạnh đáy bằng 2a là:
\(V = a{\left( {2a} \right)^2}.\frac{{\sqrt 3 }}{4} = {a^3}\sqrt 3 \).
Câu 15:
Cho hàm số y = log2x2. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
TXĐ: D = ℝ \ {0}
Ta có: y = log2x2
\( \Rightarrow y' = \frac{{{{\left( {{x^2}} \right)}^\prime }}}{{{x^2}\ln 2}} = \frac{{2x}}{{{x^2}\ln 2}}\)
Ta thấy y’ > 0 ⇔ x > 0 nên hàm số đồng biến trên (0; +∞)
y’ < 0 ⇔ x < 0 nên hàm số nghịch biến trên (−∞; 0)
Lại có: \(\mathop {\lim }\limits_{x \to \, \pm \,\infty } y = + \infty \) nên hàm số đã cho không có tiệm cận ngang
Đồ thị hàm số có một tiệm cận đúng là x = 0.
Vậy đáp án C là khẳng định sai.
Câu 16:
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình 2f(x2 – 1) – 5 = 0 là:
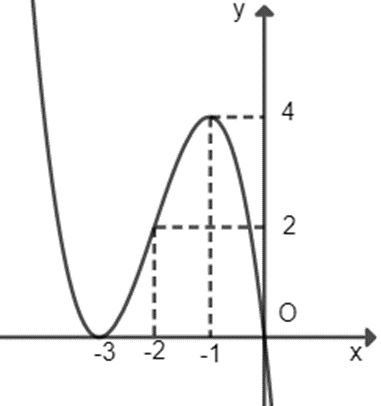
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
2f(x2 – 1) – 5 = 0
Đặt t = x2 – 1 (t ≥ −1)
Phương trình (1) trở thành
2f(t) – 5 = 0
\( \Leftrightarrow \left( t \right) = \frac{5}{2}\)
\( \Leftrightarrow \left[ \begin{array}{l}t = a(a < - 3)\\t = b\left( {b \in \left\{ { - 2; - 1} \right\}} \right)\\t = c\left( {c \in \left\{ { - 1;0} \right\}} \right)\end{array} \right.\)
Ta có t = c (thỏa mãn)
⇒ c = x2 – 1 \( \Leftrightarrow x = \pm \sqrt {c + 1} \)
Vậy số nghiệm thực của phương trình (1) là 2.
Câu 17:
Cho tứ giác ABCD có a là góc nhọn tạo bởi hai đường chéo. Chứng minh rằng \({S_{ABCD}} = \frac{1}{2}.AC.BD.\sin a\).
 Xem đáp án
Xem đáp án
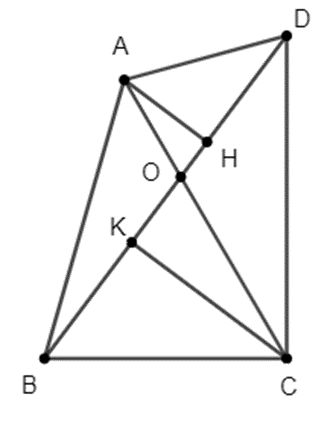
Gọi O là giao điểm hai đường chéo AC và BD và \(\widehat {AOD} = \widehat {BOC} = a < 90^\circ \)
Kẻ AH và CK vuông góc với BD. Ta có:
\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}} = \frac{1}{2}.BD.AH + \frac{1}{2}.BD.CK\)
\( = \frac{1}{2}.BD.\left( {AH + CK} \right)\) (1)
Lại có AH = OA.sina; CK = OC.sina
Do đo AH + CK = (OA + OC).sina = AC.sina (2)
Từ (1) và (2) suy ra \({S_{ABCD}} = \frac{1}{2}.AC.BD.\sin a\)
Câu 18:
Giá trị của tan30° + cot30° bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: tan30° + cot30° \( = \frac{1}{{\sqrt 3 }} + \sqrt 3 = \frac{1}{{\sqrt 3 }} + \frac{3}{{\sqrt 3 }} = \frac{4}{{\sqrt 3 }}\).
Câu 19:
Tập nghiệm của phương trình \({5^x}{.8^{\frac{{x - 1}}{x}}} = 500\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
\({5^x}{.8^{\frac{{x - 1}}{x}}} = 500 = {2^2}{.5^3}\)
\( \Leftrightarrow {5^x}{.2^{\frac{{3\left( {x - 1} \right)}}{x}}} = {2^2}{.5^3}\)
\( \Leftrightarrow {2^{\frac{{3\left( {x - 1} \right)}}{x} - 2}} = {5^{x - 3}}\)
\( \Leftrightarrow {\log _2}{2^{\frac{{x - 3}}{x}}} = {\log _2}{5^{3 - x}}\)
\( \Leftrightarrow \frac{{x - 3}}{x} = \left( {3 - x} \right){\log _2}5\)
\( \Leftrightarrow \left( {x - 3} \right)\left( {\frac{1}{x} + {{\log }_2}5} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\\frac{1}{x} + {\log _2}5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \frac{{ - 1}}{{{{\log }_2}5}} = - {\log _5}2\end{array} \right.\).
Vậy phương trình đã cho có nghiệm là x = 3 hoặc x = −log52.
Câu 20:
Giải phương trình \(\sin 3x - \frac{2}{{\sqrt 3 }}{\sin ^2}x = 2\sin x.\cos 2x\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
\(\sin 3x - \frac{2}{{\sqrt 3 }}{\sin ^2}x = 2\sin x.\cos 2x\)
\( \Leftrightarrow \sqrt 3 \sin 3x - 2{\sin ^2}x = \sqrt 3 \left( {\sin 3x - \sin x} \right)\)
\( \Leftrightarrow \sqrt 3 \sin 3x - 2{\sin ^2}x = \sqrt 3 \sin 3x - \sqrt 3 \sin x\)
\( \Leftrightarrow \sin x\left( {2\sin x - \sqrt 3 } \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\sin x = \frac{{\sqrt 3 }}{2}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)
Vậy phương trình đã cho có các họ nghiệm là: x = kp; \(x = \frac{\pi }{3} + k2\pi \); \(x = \frac{{2\pi }}{3} + k2\pi \) (k ∈ ℤ).
Câu 21:
Cho hàm số y = f(x) có bảng biến thiên như sau:
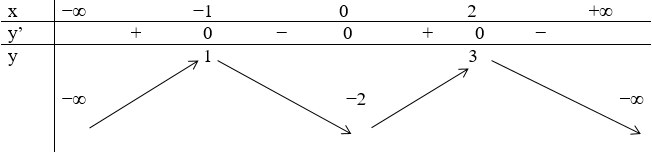
Số nghiệm thực của phương trình 2f(x) + 5 = 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Số nghiệm của phương trình 2f(x) + 5 = 0 \( \Leftrightarrow f(x) = - \frac{5}{2}\) là số giao điểm của đường thẳng \(y = - \frac{5}{2}\) và đồ thị hàm số y = f(x)
Ta có BBT:
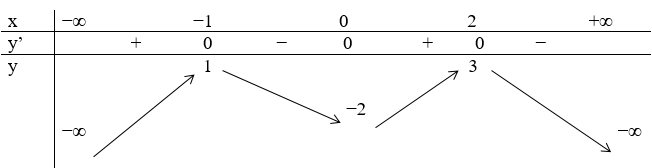
Dựa vào BBT ta thấy đường thẳng \(y = - \frac{5}{2}\) cắt đồ thị hàm số y = f(x) tại hai điểm phân biệt.
Do đó 2f(x) + 5 = 0 có hai nghiệm phân biệt.
Câu 22:
Tổng các nghiệm của phương trình 4x – 3.2x+2 + 32 = 0 bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
4x – 3.2x+2 + 32 = 0
⇔ (2x)2 – 12.2x + 32 = 0
⇔ (2x – 8)(2x – 4) = 0
\( \Leftrightarrow \left[ \begin{array}{l}{2^x} = 8\\{2^x} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\end{array} \right.\)
Vậy tập nghiệm của phương trình là: S = {3; 2}
Vậy tổng các nghiệm của phương trình là 3 + 2 = 5.
Câu 23:
Tập nghiệm của bất phương trình 4x – 3.2x+2 + 32 ≤ 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đặt t = 2x > 0. Khi đó bất phương trình trở thành:
t2 – 12t + 32 ≤ 0
⇔ 4 ≤ t ≤ 8
⇒ 4 ≤ 2x ≤ 8
⇔ 2 ≤ x ≤ 3
Vậy tập nghiệm của bất phương trình đã cho là: [2; 3].
Câu 24:
Chọn mệnh đề sai trong các mệnh đề dưới đây:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Không thể tồn tại khối chóp tứ giác đều là khối đa diện đều.
Vậy mệnh đề sai là mệnh đề B.
Câu 25:
Giải bất phương trình sau: \({\log _{\frac{1}{2}}}\left( {{4^x} + 4} \right) \ge {\log _{\frac{1}{2}}}\left( {{2^{2x + 1}} - {{3.2}^x}} \right)\).
 Xem đáp án
Xem đáp án
\({\log _{\frac{1}{2}}}\left( {{4^x} + 4} \right) \ge {\log _{\frac{1}{2}}}\left( {{2^{2x + 1}} - {{3.2}^x}} \right)\)
⇔ 4x – 3.2x – 4 ≥ 0
\( \Leftrightarrow \left[ \begin{array}{l}{2^x} \le - 1\\{2^x} \ge 4\end{array} \right.\)
⇔ 2x ≥ 4
⇔ x ≥ 2.
Vậy bất phương trình đã cho có tập nghiệm là [2; +∞)
Câu 26:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
5x + 251-x = 6
⇔ 5x + 52(1-x) = 6
\( \Leftrightarrow {5^x} + \frac{{{5^2}}}{{{5^{2x}}}} = 6\)
⇔ 53x + 25 = 6.52x
Đặt t = 5x > 0
Khi đó phương trình trở thành:
t3 – 6t2 + 25 = 0
⇔ (t – 5)(t2 – t – 5) = 0
\( \Leftrightarrow \left[ \begin{array}{l}t = 5\\t = \frac{{1 + \sqrt {21} }}{2}\\t = \frac{{1 - \sqrt {21} }}{2}\end{array} \right.\)
Vì t > 0 nên ta có: \(\left[ \begin{array}{l}t = 5\\t = \frac{{1 + \sqrt {21} }}{2}\end{array} \right.\)
Với t = 5 ⇒ 5x = 5 ⇔ x = 1
Với \(t = \frac{{1 + \sqrt {21} }}{2} \Rightarrow {5^x} = \frac{{1 + \sqrt {21} }}{2} \Leftrightarrow x = {\log _5}\left( {\frac{{1 + \sqrt {21} }}{2}} \right)\)
Vậy tích các nghiệm của phương trình bằng: \({\log _5}\left( {\frac{{1 + \sqrt {21} }}{2}} \right)\).
Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với \(AB = 2a\sqrt 3 \); BC = 2a. Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với mặt phẳng đáy (ABCD) một góc 60°. Khoảng cách từ D đến (SBC) tính theo a bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
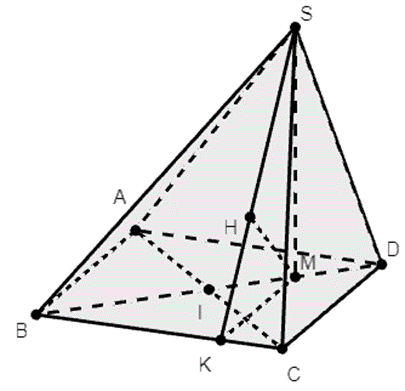
Ta có SB tạo với mp (ABCD) là: \(\widehat {SBM} = 60^\circ \)
\(BM = \frac{3}{4}BD = 3a\)
\(SM = BM.\tan 60^\circ = 3\sqrt 3 a\)
\(d\left( {D,\left( {SBC} \right)} \right) = \frac{4}{3}d\left( {M,\left( {SBC} \right)} \right) = \frac{4}{3}MH\)
Xét ∆SMK vuông tại M có:
\(\frac{1}{{M{H^2}}} = \frac{1}{{M{K^2}}} + \frac{1}{{M{S^2}}}\)
\( = \frac{1}{{{{\left( {\frac{3}{4}.2\sqrt 3 a} \right)}^2}}} + \frac{1}{{{{\left( {3\sqrt 3 a} \right)}^2}}} = \frac{5}{{27{a^2}}}\)
\( \Rightarrow MH = \sqrt {\frac{{27}}{5}} a\)
Vậy \(d\left( {D,\left( {SBC} \right)} \right) = \frac{3}{4}MH = \frac{{4\sqrt {15} a}}{5}\).
Câu 28:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên (SBC) là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
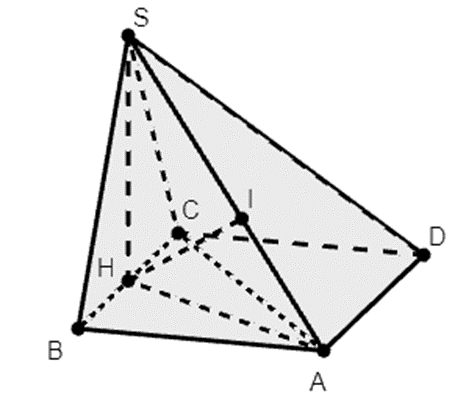
Gọi H là trung điểm của BC. Khi đó SH ⊥ (ABCD).
Do tam giác ABC vuông cân tại A nên AH ⊥ BC và \(AH = \frac{a}{2}\).
Dựng điểm D sao cho ABCD là hình bình hành.
Khi đó d(SA, BC) = d(BC, (SAD)) = d(H, (SAD)).
Kẻ HI ⊥ SA.
Khi đó d(H, (SAD)) = HI \( = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{a}{2}}}{a} = \frac{{a\sqrt 3 }}{4}\).
Câu 29:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
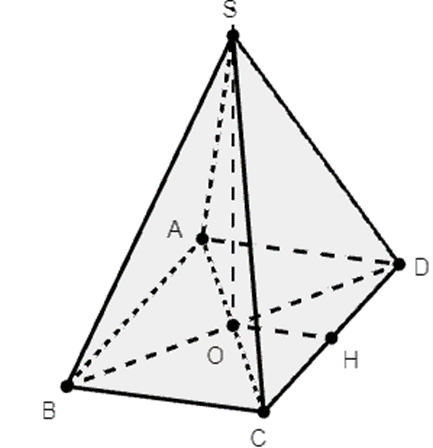
Ta có \(R = OH = \frac{a}{2}\)
\(SH = \sqrt {S{O^2} + O{H^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {17} }}{2}\)
Vậy \({S_{xq}} = \pi .\frac{a}{2}.\frac{{a\sqrt {17} }}{2} = \frac{{\pi {a^2}\sqrt {17} }}{4}\)
Câu 30:
Tìm nghiệm của phương trình 3x – 1 = 9.
 Xem đáp án
Xem đáp án
3x – 1 = 9
⇔ 3x – 1 = 32
⇔ x – 1 = 2
⇔ x = 3
Vậy x = 3 là nghiệm của phương trình.
Câu 31:
Gọi S là nghiệm của phương trình ln(3ex – 2) = 2x. Số tập con của S bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có ln(3ex – 2) = 2x
⇔ 3ex – 2 = e2x
⇔ e2x – 3ex + 2 = 0
\( \Leftrightarrow \left[ \begin{array}{l}{e^x} = 1\\{e^x} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \ln 2\end{array} \right.\)
Vậy S có 2 phần tử nên có tất cả 22 = 4 tập con.
Câu 32:
Tập nghiệm của bất phương trình ln(1 – x) < 0:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: ln(1 – x) < 0
⇔ 0 < 1 – x < e0
⇔ 0 < x < 1
Vậy tập nghiệm của bất phương trình là (0; 1)
Câu 33:
Với các chữ số 0; 1; 2; 3; 4; 5 có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Gọi số lẻ đang xét có dạng \(\overline {abcd} \)
Ta có:
d ∈ {1; 3; 5}
a ∈ {1; 2; 3; 4; 5}
b và c ∈ {0; 1; 2; 3; 4; 5}
Khi đó ta có:
• d có 3 cách chọn
• a có 4 cách chọn
• b có 4 cách chọn
• c có 3 cách chọn
Vậy các số lẻ có thể lập được là 3.4.4.3 = 144.
Câu 34:
Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 ta lập được bao nhiêu số tự nhiên gồm 10 chữ số đôi một khác nhau?
 Xem đáp án
Xem đáp án
Xét số tự nhiên có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}{a_8}{a_9}{a_{10}}} \).
TH1: a1 có thể bằng 0 hoặc khác 0.
Với a1 có thể bằng 0 hoặc khác 0, mỗi số có dạng trên là một hoán vị của 10 chữ số đã cho.
Do đó, số các số có thể lập được trong trường hợp 1 là:
P10 = 10! (số).
Trường hợp 2: a1 = 0.
Vì a1 = 0 cố định nên 9 chữ số sau a1 đều khác 0 và chỉ có 9 chữ số đó thay đổi.
Suy ra, mỗi số có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}{a_8}{a_9}{a_{10}}} \) là một hoán vị của 9 chữ số khác 0 đã cho.
Do đó, số các số có thể lập được trong trường hợp 2 là:
P9 = 9! (số).
Vậy số các số tự nhiên có 10 chữ số đôi một khác nhau có thể lập được là:
10! – 9! = 3 265 920 (số).
Câu 35:
Cho hai đường tròn bằng nhau (O; R) và (O’; R’) phân biệt. Có bao nhiêu phép vị tự biến (O; R) thành (O’; R’)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì O và O’ riêng biệt, R = R’
Suy ra chỉ có duy nhất 1 phép vị tự biến (O; R) thành (O’; R’).
Câu 36:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc \(\widehat {BAD} = 60^\circ \); \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi a là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
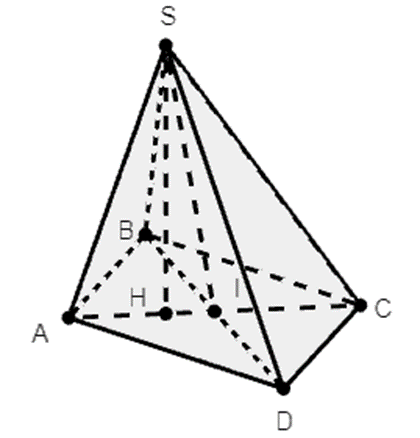
Từ giả thiết suay ra tam giác ABD đều cạnh a.
Gọi H là hình chiếu của S trên mặt phẳng (ABCD).
Do SA = SB = SC nên suy ra H cách đều các đỉnh của tam giác ABD hay H là tâm của tam giác đều ABD.
Suy ra \(HI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{6}\) và \(SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{6}\)
Vì ABCD là hình thoi nên HI ⊥ BD
Tam giác SBD cân tại S nên SI ⊥ BD
Do đó \(\widehat {\left( {\left( {SBD} \right),\,\,\left( {ABCD} \right)} \right)} = \widehat {\left( {SI,\,\,AI} \right)} = \widehat {SIH}\)
Trong tam giác vuông SHI, có \(\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \sqrt 5 \).
Câu 37:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
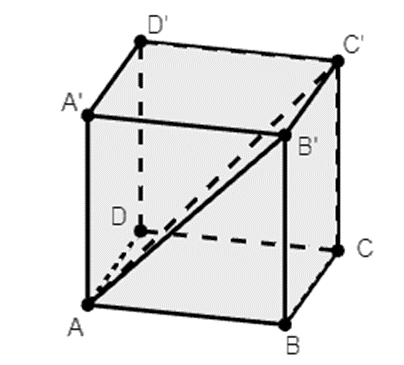
Ta có: C’B ⊥ (ABB’A’) nên suy ra ∆AB’C’ vuông tại B’.
(AB’)2 = a2 + c2
Khi đó ta có: \(AC' = \sqrt {{{(AB')}^2} + {{(B'C')}^2}} \)
\( = \sqrt {{a^2} + {c^2} + {b^2}} \).
Câu 38:
 Xem đáp án
Xem đáp án
Ta có: n3 + 5n = n3 – n + 6n = n(n2 – 1) + 6n
= n(n – 1)(n + 1) + 6n
Vì n là số nguyên dương nên suy ra:
Tích của ba số nguyên dương liên tiếp: n – 1; n; n + 1 chia hết cho 2 và 3
Nên n.(n – 1)(n + 1) chia hết cho 6.
Mà 6n chia hết cho 6 nên suy ra:
n(n – 1)(n + 1) + 6n chia hết cho 6.
Suy ra với mọi số nguyên dương ta luôn có n3 + 5n chia hết cho 6 (đpcm)
Câu 39:
Cho x là số thực dương, số hạng không chứa x trong khai triển nhị thức \({\left( {x + \frac{2}{{\sqrt x }}} \right)^{30}}\) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \({\left( {x + \frac{2}{{\sqrt x }}} \right)^{30}} = \sum\limits_{k = 0}^{30} {C_{30}^k{{\left( x \right)}^{30 - k}}.{{\left( {\frac{2}{{\sqrt x }}} \right)}^k}} \)
\( = \sum\limits_{k = 0}^{30} {C_{30}^k.{{\left( 2 \right)}^k}.{{\left( x \right)}^{\frac{{60 - 3k}}{2}}}} \)
Số hạng không chứa x tương ứng \(\frac{{60 - 3k}}{2} = 0 \Leftrightarrow k = 20\)
Vậy số hạng không chứa x là: \({2^{20}}\,.\,C_{30}^{20} = {2^{20}}\,.\,C_{30}^{10}\).
Câu 40:
Giá trị lớn nhất của hàm số y = x4 – 4x2 + 9 trên đoạn [−2; 3] bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hàm số đã cho xác định và liên tục trên đoạn [−2; 3]
Ta có y¢ = 4x3 – 8x
\(y' = 0 \Leftrightarrow 4{x^3} - 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\)
Ta có: f(−2) = 9; f(3) = 54; f(0) = 9; \(f\left( { - \sqrt 2 } \right) = 5\); \(f\left( {\sqrt 2 } \right) = 5\)
Vậy giá trị lớn nhất của hàm số trên đoạn [−2; 3] bằng f(3) = 54.
Câu 41:
Giá trị lớn nhất của hàm số y = −x3 + 3x2 + 24x – 7 trên đoạn [−3; 3] bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: y¢ = −3x2 + 6x + 24 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = - 2 \in [ - 3;3]\\x = 4 \notin [ - 3;3]\end{array} \right.\)
y(−3) = −25; y(−2) = −35; y(3) = 65.
Vậy giá trị cần tìm là 65.
Câu 42:
Giá trị nhỏ nhất của hàm số y = x3 + 2x2 – 7x trên đoạn [0; 4] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
TXĐ: D = ℝ
Hàm số liên tục trên đoạn [0; 4]
Ta có: y¢ = 3x2 + 4x – 7 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 1 \in [0;4]\\x = - \frac{7}{3} \notin [0;4]\end{array} \right.\)
Khi đó y(0) = 0; y(1) = −4; y(4) = 68
Vậy giá trị nhỏ nhất cần tìm là: −4.
Câu 43:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(\widehat {ABC} = 120^\circ \); ∆SAB đều và nằm trong mặt phẳng vuôn góc với mặt đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
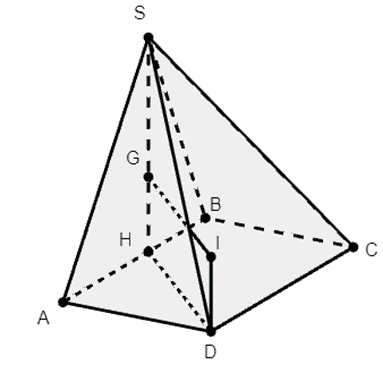
Gọi H là trung điểm của AB, khi đó SH ⊥ AB
Lại có (SAB) ⊥ (ABCD) suy ra SH ⊥ (ABCD)
Ta có: \(\widehat {ABC} = 120^\circ \Rightarrow \widehat {BAD} = \widehat {BCD} = 60^\circ \)
Suy ra, tam giác BAD; BCD là tam giác đều.
Do đó DA = DB = DC.
Khi đó, D là tâm đường tròn ngoại tiếp tam giác ABC.
Vì tam giác SAB; ABD là tam giác đều nên DH ⊥ (SAB)
Trục đường tròn ngoại tiếp tam giác SAB cắt đường thẳng Dt (Dt // SH) tại I nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Ta có: \(DH = \frac{{a\sqrt 3 }}{2} = IG\); \(SG = \frac{2}{3}SH = \frac{{a\sqrt 3 }}{3}\)
\( \Rightarrow R = \sqrt {I{G^2} + S{G^2}} = \frac{{a\sqrt {39} }}{6}\).
Câu 44:
Một hộp chứa 5 bi xạnh, 7 bi đỏ và 8 bi vàng. Lấy ngẫu nhiên 8 viên bi từ hộp. Tính xác suất để 8 viên bi lấy ra có đủ cả 3 màu.
 Xem đáp án
Xem đáp án
Lẫy ngẫu nhiên 8 bi từ hộp, không gian mẫu có: \[\left| \Omega \right| = C_{20}^8 = 125\,\,970\].
Số cách chọn 8 bi không có đủ cả 3 màu:
TH1: Chọn 8 bi chỉ có 1 màu (chỉ chọn được màu vàng): \(C_8^8 = 1\)
TH2: Chọn 8 bi có 2 màu: \(C_{12}^8 + C_{13}^8 + C_{15}^8 - 2C_8^8 = 8215\)
Gọi A là biến cố chọn 8 bi không đủ 3 màu
\( \Rightarrow \left| {{\Omega _A}} \right| = 8215 + 1 = 8216\)
Xác suất
\(P\left( A \right) = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}} = \frac{{8216}}{{C_{20}^8}} = \frac{{316}}{{4845}}\)
Gọi B là biến cố 8 bi được chọn có đủ cả 3 màu
\( \Rightarrow B = \overline A \)
Vậy xác suất: \(P\left( B \right) = 1 - P\left( A \right) = \frac{{4529}}{{4845}}\).
Câu 45:
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (A) 4x – 3y – 7z + 3 = 0 và điểm I(1; −1; 2). Phương trình mặt phẳng đối xứng với (A) qua I là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Do (B) đối xứng với (A) qua O nên (B) // (A)
Suy ra (B): 4x – 3y – 7z + D = 0 với D ≠ 3.
Chọn M(0; 1; 0) ∈ (A)
Suy ra tọa độ điểm N đối xứng với M qua I là: N(2; −3; 2) ∈ (B)
Thay toạn độ điểm N vào phương trình (B) ta được: D = 11
Vậy phương trình mặt phẳng (B) là: 4x – 3y – 7z + 11 = 0.
Câu 46:
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): mx + y – 2z – 2 = 0 và (Q): x – 3y + mz + 5 = 0. Tìm tất cả các giá trị thực của m để hai mặt phẳng đã cho vuông góc với nhau.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có (P) ⊥ (Q) khi và chỉ khi \(\overrightarrow {{n_{\left( P \right)}}} \,.\,\overrightarrow {{n_{\left( Q \right)}}} = 0\)
⇔ m.1 + 1(−3) + (−2).m = 0
⇔ −m – 3 = 0
⇔ m = −3
Vậy với m = −3 thỏa mãn yêu cầu bài toán.
Câu 47:
Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4 cm.
 Xem đáp án
Xem đáp án
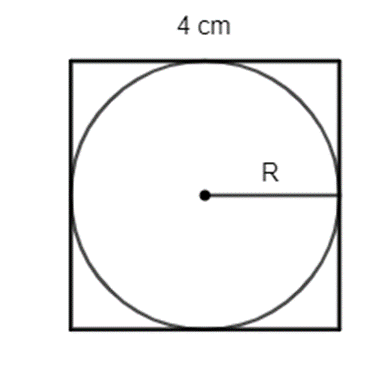
Hình tròn nội tiếp hình vuông có cạnh 4 cm thì có R = 2 cm.
Vậy diện tích hình tròn là: pR2 = 4p (cm2)
Câu 48:
Phân tích đa thức thành nhân tử:
a) x2 – 4x + 4;
b) x3 + 9x2 + 27x + 27.
 Xem đáp án
Xem đáp án
a) x2 – 4x + 4 = x2 – 2.x.2 + 22 = (x – 2)2.
b) x3 + 9x2 + 27x + 27 = x3 + 3.x2 . 3 + 3.x.32 + 33 = (x + 3)3.
Câu 49:
Tập xác định của hàm số y = log3(x2 + 2x) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hàm số đã cho xác định khi:
x2 + 2x > 0
\( \Leftrightarrow \left[ \begin{array}{l}x > 0\\x < - 2\end{array} \right.\)
Vậy D = (−∞; −2) È (0; +∞).
Câu 50:
Cho tập hợp A = {0; 1; 2; 3; 4} và B = {x ∈ ℕ| x < 5}. Trong các kết luận sau, kết luận nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \(\left\{ \begin{array}{l}x \in \mathbb{N}\\x < 5\end{array} \right.\) ⇒ x ∈ {0; 1; 2; 3; 4}
⇒ B = {0; 1; 2; 3; 4} ⇒ A = B.
Câu 51:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Số cách xếp ngẫu nhiên là 10!.
Ta tìm số cách xếp thoả mãn:
Đánh số hàng từ 1 đến 10. Có hai khả năng:
• 5 nam xếp vị trí lẻ và 5 nữ xếp vị trí chẵn có 5! . 5! = 1202
• 5 nam xếp vị trí chẵn và 5 nữ xếp vị trí lẻ có 5! . 5! = 1202
Theo quy tắc cộng ta có: 1202 + 1202 = 2 . 1202 cách sắp xếp thỏa mãn.
Vậy xác suất cần tính: \(\frac{{2{{(5!)}^2}}}{{10!}} = \frac{1}{{126}}\).
