Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
A. 6a3;
B. \(\frac{{4{a^3}\sqrt 3 }}{9}\);
C. \(4{a^3}\sqrt 3 \);
D. \(\frac{{4{a^3}\sqrt 3 }}{3}\).
Giải bởi Vietjack
Đáp án đúng là: D
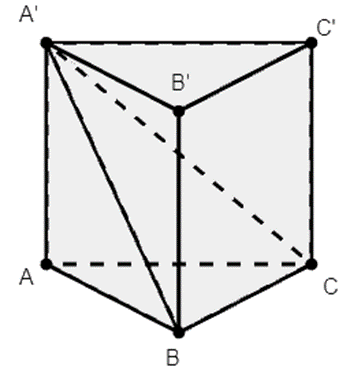
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot \left( {A'BA} \right) \Rightarrow \widehat {A'BA} = 30^\circ \)
Khi đó \(AA' = AB.\tan 30^\circ = \frac{{2a}}{{\sqrt 3 }}\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \frac{{4{a^2}}}{2}.\frac{{2a}}{{\sqrt 3 }} = \frac{{4{a^3}\sqrt 3 }}{3}\)
Cho tứ giác ABCD có a là góc nhọn tạo bởi hai đường chéo. Chứng minh rằng \({S_{ABCD}} = \frac{1}{2}.AC.BD.\sin a\).
Giá trị nhỏ nhất của hàm số y = x3 + 2x2 – 7x trên đoạn [0; 4] bằng
Quãng đường AB gồm một đoạn lên dốc dài 4 km và một đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
Tập nghiệm của phương trình \({5^x}{.8^{\frac{{x - 1}}{x}}} = 500\) là
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(\widehat {ABC} = 120^\circ \); ∆SAB đều và nằm trong mặt phẳng vuôn góc với mặt đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là:
Tìm một số tự nhiên có hai chữ số,biết rằng nếu viết thêm chữ số 6 vào bên trái số đó ta được một số lớn gấp 13 lần số đã cho.
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a bằng:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
Cho phương trình (m + 1).16x − 2( 2m − 3) .4x + 6m + 5 = 0 với m là tham số thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng (a; b). Tính P = a.b.
