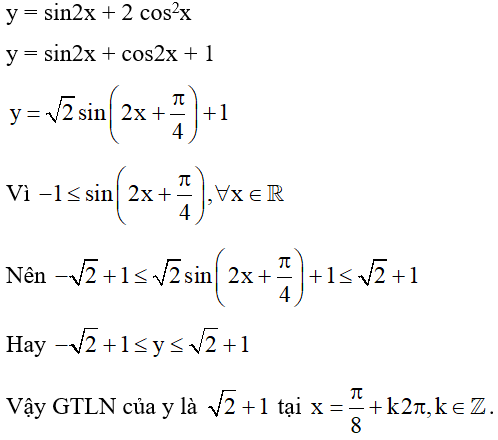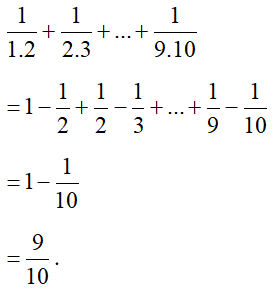- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 96)
-
12968 lượt thi
-
94 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Tìm x biết: x3 + 27 + (x + 3)(x – 9) = 0.
 Xem đáp án
Xem đáp án
Ta có: x3 + 27 + (x + 3)(x – 9) = 0
(x + 3)(x2 – 3x + 9) + (x + 3)(x – 9) = 0
(x + 3)(x2 – 3x + 9 + x – 9) = 0
(x + 3)(x2 – 2x) = 0
(x + 3).x.(x – 2) = 0
Suy ra x = 0 hoặc x = – 3 hoặc x = 2.
Vậy x ∈ {-3; 0; 2}.
Câu 2:
Tìm x biết: x3 + 27 + (x + 3)(x – 9) = 0.
 Xem đáp án
Xem đáp án
Ta có: x3 + 27 + (x + 3)(x – 9) = 0
(x + 3)(x2 – 3x + 9) + (x + 3)(x – 9) = 0
(x + 3)(x2 – 3x + 9 + x – 9) = 0
(x + 3)(x2 – 2x) = 0
(x + 3).x.(x – 2) = 0
Suy ra x = 0 hoặc x = – 3 hoặc x = 2.
Vậy x ∈ {-3; 0; 2}.
Câu 3:
 Xem đáp án
Xem đáp án
x3 – y3 + x – y
= (x3 – y3) + (x – y)
= (x – y)(x2 + xy + y2) + (x – y)
= (x – y)(x2 + xy + y2 + 1).
Câu 4:
Cho x + y = 3 và xy = 2. Tính x3 + y3.
 Xem đáp án
Xem đáp án
Ta có: x3 + y3
= (x + y)(x2 – xy + y2)
= (x + y)[(x2 + 2xy + y2) – 3xy]
= (x + y)[(x2 + 2xy + y2) – 3xy]
= (x + y)[(x + y)2 – 3xy]
Thay x + y = 3 và xy = 2 vào đa thức trên ta có:
x3 + y3 = 3.(32 – 3.2) = 3.(9 – 6) = 3.3 = 9.
Câu 5:
Phân tích đa thức thành nhân tử: x3 + y3 + 2x2 – 2xy + 2y2.
 Xem đáp án
Xem đáp án
x3 + y3 + 2x2 – 2xy + 2y2
= (x3 + y3) + (2x2 – 2xy + 2y2)
= (x + y)(x2 – xy + y2) + 2(x2 – xy + y2)
= (x + y + 2)(x2 – xy + y2).
Câu 6:
Phân tích đa thức thành nhân tử: x4 – 25x2 + 20x – 4.
 Xem đáp án
Xem đáp án
x4 – 25x2 + 20x – 4
= x4 – 5x3 + 2x2 + 5x3 – 25x2 + 10x – 2x2 + 10x – 4
= x2(x2 – 5x + 2) + 5x(x2 – 5x + 2) – 2(x2 – 5x + 2)
= (x2 – 5x + 2)(x2 + 5x – 2).
Câu 7:
Phân tích đa thức thành nhân tử: x4 + 6x3 – 11x2 + 6x + 1.
 Xem đáp án
Xem đáp án
x4 + 6x3 – 11x2 + 6x + 1
= (x4 + 1) + (6x3 + 6x) – 11x2
= (x2 + 1)2 – 2x2 + 6x(x2 + 1) - 11x2
= (x2 + 1 + 3x)2 -
=
.
Câu 8:
Cho hàm số y = x4 + mx3 – 2x2 – 3mx + 1. Xác định m để hàm số có 2 cực tiểu.
 Xem đáp án
Xem đáp án
Ta có: y’ = 4x3 + 3mx2 – 4x – 3m
Xét y’ = 0
⇔ 4x3 + 3mx2 – 4x – 3m = 0
⇔ (x – 1)[4x2 + (4 + 3m)x + 3m] = 0
⇔
Hàm số có 2 cực tiểu ⇔ y có 3 cực trị ⇔ y′ = 0 có 3 nghiệm phân biệt
Suy ra: (2) có 2 nghiệm phân biệt khác 1
Vậy khi thì hàm số có 2 cực tiểu.
Câu 9:
Phân tích đa thức x8 + x4 + 1 thành nhân tử ta được?
 Xem đáp án
Xem đáp án
x8 + x4 + 1
= x8 + 2x4 + 1 – x4
= (x8 + 2x4 + 1) – x4
= [(x4)2 + 2.x4.1 + 12] – x4
= (x4 + 1)2 – (x2)2
= (x4 + 1 – x2)(x4 + 1 + x2)
= (x4 – x2 + 1)(x4 + 2x2 – x2 + 1)
= (x4 – x2 + 1)[((x2)2 + 2.1.x2 + 1) – x2]
= (x4 – x2 + 1)[(x2 + 1)2 – x2]
= (x4 – x2 + 1)(x2 + 1 – x)(x2 + 1 + x)
= (x4 – x2 + 1)(x2 – x + 1)(x2 + x + 1).
Câu 11:
 Xem đáp án
Xem đáp án
x – 3 = (3 - x)2
⇔ x – 3 = 9 – 6x + x2
⇔ x2 – 7x + 12 = 0
⇔ x2 – 3x – 4x + 12 = 0
⇔ x(x – 3) – 4(x – 3) = 0
⇔ (x – 3)(x – 4) = 0
⇔
Vậy x = 3 hoặc x = 4.
Câu 14:
 Xem đáp án
Xem đáp án
A = n3 + (n + 1)3 + (n + 2)3
= n3 + n3 + 3n2 + 3n + 1 + n3 + 6n2 + 12n + 8
= 3n3 + 9n2 + 15n + 9
= 3n2 (n + 1) + 6n ( n + 1) + 9 (n +1)
= 3 (n + 1)(n2 + 2n + 3)
=3(n + 1)[n (n + 2) + 3]
= 3n (n + 1)(n + 2) + 9( n + 1)
Ta có: n; n + 1; n + 2 là 3 số tự nhiên liên tiếp
⇒ 3n(n + 1)(n + 2) ⋮ 9
Mặc khác: 9(n + 1) ⋮ 9
⇒ A = 3n (n + 1)(n + 2) + 9(n + 1) ⋮ 9.
Vậy A = n3 + (n + 1)3 + (n + 2)3 ⋮ 9.
Câu 15:
Cho p, q là số nguyên tố và phương trình x2 − px + q = 0 có nghiệm nguyên dương. Tìm p, q.
 Xem đáp án
Xem đáp án
Để phương trình đã cho có nghiệm nguyên dương thì Δ = p2 − 4q là số chính phương.
Đặt p2 − 4q = k2
⇔ 4q = (p − k)(p + k) với k là số tự nhiên.
Do p − k, p + k cùng tính chẵn, lẻ mà tích của chúng chẵn nên hai số này cùng chẵn.
Mặt khác p − k < p + k và q là số nguyên tố nên:
p − k = 2 và p + k = 2q hoặc p − k = 4 và p + k = q
Nếu p − k = 4 và p + k = q thì q chẵn do đó q = 2 (vô lí vì p + k > p − k).
Nếu p − k = 2 và p + k = 2q thì 2p = 2q + 2 tức p = q + 1.
Do đó q chẵn tức q = 2. Suy ra p = 3.
Thử lại ta thấy phương trình: x2 − 3x + 2= 0 có nghiệm nguyên dương x = 1 và x = 2.
Vậy p = 3; q = 2.
Câu 16:
Nếu , và g(x) > 0, ∀x ≠ x0 thì có kết quả nào sau đây?
A. -∞.
B. -5.
C. 0.
D. 5.
 Xem đáp án
Xem đáp án
Đáp án A
.
Câu 17:
 Xem đáp án
Xem đáp án
⇔ 168n + 84 = 167n + 334
⇔ n = 250
Vậy số là số hạng thứ 250 của dãy số.
Câu 19:
Cho hàm số y = (m - 3)x + 3. Tìm các giá trị của m để hàm số nghịch biến trên ℝ.
 Xem đáp án
Xem đáp án
Để hàm số nghịch biến trên ℝ thì m – 3 < 0
Hay m < 3.
Vậy m < 3 thì hàm số nghịch biến trên ℝ.
Câu 20:
Tìm GTLN và GTNN của hàm số .
 Xem đáp án
Xem đáp án
TXĐ: 2cosx – sinx + 4 ≠ 0 ⇒ x ∈ ℝ
Khi đó: y(2cosx – sinx + 4) = 2sinx + cosx + 3
⇔ (2y – 1)cosx – (y + 2)sinx = 3 – 4y (*)
Để (*) có nghiệm thì:
(3 – 4y)2 ≤ (2y – 1)2 + [-(y + 2)]2
⇔
Từ đây suy ra .
Câu 25:
 Xem đáp án
Xem đáp án
Ta có:
Bảng biến thiên:
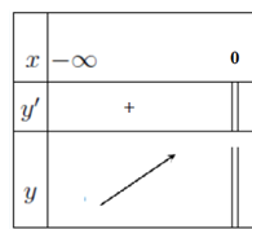
Vậy hàm số đồng biến trên mỗi khoảng (-∞; 0).
Câu 26:
Tìm x, y nguyên biết xy + 3x – y = 6.
 Xem đáp án
Xem đáp án
Ta có: xy + 3x – y = 6
⇔ x(y + 3) – (y + 3) = 6 – 3
⇔ (x – 1)(y + 3) = 3
Suy ra: x – 1 và y + 3 thuộc Ư(3)
Ta có bảng sau:
|
x – 1 |
1 |
–1 |
3 |
–3 |
|
y + 3 |
3 |
–3 |
1 |
–1 |
|
x |
2 |
0 |
4 |
–2 |
|
y |
0 |
–6 |
–2 |
–4 |
Vậy (x; y) ∈ {(2; 0), (0; –6), (4; –2), (–2; –4)}.
Câu 27:
Xác định tọa độ đỉnh của parabol y = ax2 + bx + c (a ≠ 0).
 Xem đáp án
Xem đáp án
Ta có: y = ax2 + bx + c
Xét ∆ = b2 – 4ac
Đỉnh của parobol có hoành độ
Khi đó:
Vậy tọa độ đỉnh của parabol là .
Câu 28:
Tìm x biết x ∈ BC(15, 45) và x < 200.
 Xem đáp án
Xem đáp án
Vì 15 = 3.5
45 = 32 .5
⇒ BCNN(15, 45) = 32.5 = 45
⇒ x ∈ B(45) = {0; 45; 90; 135; 180; 225; .....}
Mà x < 200 nên x ∈ {0; 45; 90; 135; 180}.
Vậy x ∈ {0; 45; 90; 135; 180}.
Câu 29:
Cho các tập hợp A = {x ∈ ℝ|x < 3}, B = {x ∈ ℝ |1 < x ≤ 5}, C = {x ∈ ℝ|−2 ≤ x ≤ 4}. Xác định (B ∪ C)\(A ∩ C).
 Xem đáp án
Xem đáp án
A = (−∞; 3), B = (1; 5], C = [−2; 4]
(B ∪ C)\(A ∩ C) = {(1; 5] ∪ [−2; 4]} \ {(−∞; 3) ∩ [−2; 4]}
= [−2; 5] \ [−2; 3)
= [3; 5].
Câu 30:
Tìm x biết: x + (x + 2) + (x + 4) + ... + (x + 100) = 2601.
 Xem đáp án
Xem đáp án
x + (x + 2) + (x + 4) + ... + (x + 100) = 2601
(x + x + ... + x) + (2 + 4 + ... + 100) = 2601
51x + 2550 = 2601
51x = 51
x = 1
Vậy x = 1.
Câu 31:
 Xem đáp án
Xem đáp án
x2 – 6x – y2 + 9
= (x2 – 6x + 9) – y2
= (x – 3)2 – y2
= (x – 3 + y)(x – 3 – y).
Câu 32:
Tìm x biết: x2 – 6x – 7 = 0.
 Xem đáp án
Xem đáp án
x2 – 6x – 7 = 0
⇔ x2 – 7x + x – 7 = 0
⇔ x(x – 7) + (x – 7) = 0
⇔ (x – 7)(x + 1) = 0
⇔
Vậy x = 7 hoặc x = -1.
Câu 33:
Phân tích đa thức thành nhân tử: x3 – 2x2 + 2x – 1.
 Xem đáp án
Xem đáp án
x3 – 2x2 + 2x – 1
= (x3 – 1) – 2x(x – 1)
= (x – 1)(x2 + x + 1) - 2x(x – 1)
= (x – 1)(x2 + x + 1 – 2x)
= (x – 1)(x2 – x + 1).
Câu 34:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N là trung điểm của SA và SB. Tìm giao tuyến (OMN) với (ABCD).
 Xem đáp án
Xem đáp án
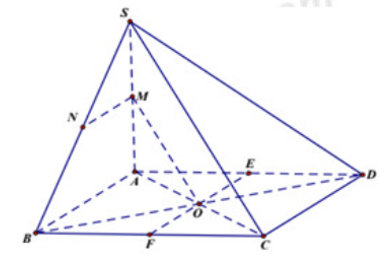
Xét tam giác SAB có MN là đường trung bình, nên MN // AB.
Hai mặt phẳng (OMN) và (ABCD) có điểm chung là O và lần lượt chứa hai đường thẳng song song MN và AB nên giao tuyến của chúng là đường thẳng đi qua O là song song với AB cắt AD, BC lần lượt tại E, F là các trung điểm của các cạnh AD, BC.
Vậy giao tuyến của (OMN) và (ABCD) là EF.
Câu 35:
Tìm x biết x : 9 = 1325 dư 8.
 Xem đáp án
Xem đáp án
x : 9 = 1325 dư 8
⇔ x – 8 = 1325 . 9
⇔ x – 8 = 11925
⇔ x = 11925 + 8
⇔ x = 11933
Vậy x = 11933.
Câu 36:
Tìm x biết x ⋮ 5 và 13 < x ≤ 78.
 Xem đáp án
Xem đáp án
x ⋮ 5 và 13 < x ≤ 78
Vì x ⋮ 5 nên x ∈ B(5) do đó x ∈ {0; 5; 10; 15; 20; 25; 30; 35; 40; ...}
Mặt khác 13 < x ≤ 78
Nên x ∈ {15; 20; 25; 30; 35; 40; 45; 50; 55; 60; 65; 70; 75}.
Câu 37:
Tìm x nhỏ nhất biết x chia hết cho 28; x chia hết cho 56; x chia hết cho 70 và 500 < x < 600.
 Xem đáp án
Xem đáp án
x ⋮ 28, x ⋮ 56, x ⋮ 70
⇒ x ∈ BC(28, 56, 70)
Ta có:
28 = 22.7
56 = 23.7
70 = 2.5.7
BCNN(28, 56, 70) = 23.5.7 = 280
BC(28, 56, 70) = B(280) = {0; 280; 560; 840;…}
Mà 500 < x < 600 nên x = 560.
Vậy x = 560.
Câu 38:
Phân tích các đa thức thành nhân tử:
a) 3x2 − 12x + 12.
b) x2 + 7x + 7y − y2.
 Xem đáp án
Xem đáp án
a) 3x2 − 12x + 12 = 3(x2 – 4x + 4) = 3(x – 2)2 = 3(x – 2)(x – 2) = (3x – 6)(x – 2)
b) x2 + 7x + 7y − y2
= (x – y)(x + y) + 7(x + y)
= (x + y)(x – y + 7)
Câu 39:
Tìm x biết x thuộc B (4) và 16 ≤ x ≤ 28 (x ∈ ℕ).
 Xem đáp án
Xem đáp án
x ∈ ℕ
x ∈ B(4)
⇒ x ∈{0; 4; 8; 12; 16; 20; 24; 28;...}
Mà 16 ≤ x ≤ 28
⇒ x ∈ {16; 20; 24; 28}
Vậy x ∈ {16; 20; 24; 28}.
Câu 40:
Với giá trị nào của m thì cặp số (2; -1) là 1 nghiệm của bất phương trình
2x − (m − 2)y > 3?
 Xem đáp án
Xem đáp án
Thay x = 2, y = -1 vào bất phương trình ta có:
2.2 – (m – 2).(-1) > 3
⇔ 4 + m – 2 > 3
⇔ m > 1
Vậy m ∈ (1; +∞) thì cặp số (2; −1) là nghiệm của bất phương trình 2x − (m − 2)y > 3.
Câu 41:
Tìm m để phương trình sau có nghiệm: 2cosx + 1 – m = 0.
 Xem đáp án
Xem đáp án
2cosx + 1 – m = 0
⇔
Vì -1 ≤ cosx ≤ 1 nên để phương trình có nghiệm thì
Vậy -1 ≤ m ≤ 3 thì phương trình có nghiệm.
Câu 42:
Cho hàm số y = (m + 5)x + 2m - 10. Với giá trị nào của m thì y là hàm số bậc nhất?
 Xem đáp án
Xem đáp án
Ta thấy hàm số bậc nhất có dạng y = ax + b (a ≠ 0)
Để y là hàm số bậc nhất thì m + 5 ≠ 0 tức m ≠ -5
Vậy với m ≠ -5 thì hàm số đã cho là hàm số bậc nhất.
Câu 43:
Chứng minh với mọi n ∈ ℕ* thì 2n + 1 là số lẻ.
 Xem đáp án
Xem đáp án
+ Nếu n là số chẵn thì 2n là số chẵn
⇒ 2n + 1 là số lẻ
+ Nếu n là số lẻ thì 2n là số chẵn
⇒ 2n + 1 là số lẻ
Vậy với mọi n ∈ ℕ* thì 2n + 1 là số lẻ.
Câu 44:
Vòng chung kết bóng đá tiểu học 2014, có 5 đội tuyển của 5 trường tham gia thi đấu theo thể thức vòng tròn 1 lượt. Đội thắng được 2 điểm, thua 0 điểm và nếu trận đấu có kết quả hòa thì mỗi đội được 1 điểm. Sau khi thi đấu người ta thấy tổng điểm của 5 đội là 21. Tính số điểm đội vô địch?
 Xem đáp án
Xem đáp án
Với 5 đội tuyển thì có số trận thi đấu là:
5.4 : 2 = 10 (trận)
Giả dụ các trận đều hòa thì tổng số điểm của hai đội mỗi trận bằng 2 nên tổng số điểm của các đội là:
2.10 = 20 (điểm)
Nhưng đề ra tổng số điểm của 5 đội là 21 điểm, mà mỗi trận không hòa thì tổng điểm của hai đội là 3 điểm, chênh lệch 1 điểm so với trận hòa. Vì vậy mà phải đổi một trận hòa với 1 trận không hòa
⇒ 10 trận thì có 9 trận hòa, 1 trận không hòa. Đội giành vô địch là đội đã thắng trong trận không hòa.
Từ đó, ta thấy đội vô địch thi đấu 4 trận thì chỉ thắng 1 trận, hòa 3 trận nên số điểm họ có là: 1.3 + 3.1 = 6 (điểm).
Câu 45:
 Xem đáp án
Xem đáp án
Lũy thừa bậc n của một số tự nhiên a, kí hiệu an, là tích của n thừa số a (n là số tự nhiên lớn hơn 1).
Nhân hai lũy thừa cùng cơ số: am . an = am+n
Chia hai lũy thừa cùng cơ số: am : an = am-n (a ≠ 0; m ≥ n).
Câu 46:
Phát biểu và viết dạng tổng quát hai tính chất chia hết của một tổng. Phát biểu các dấu hiệu chia hết cho 2, cho 3, cho 5, cho 9.
 Xem đáp án
Xem đáp án
- Tính chất 1: a ⋮ m và b ⋮ m ⇒ (a + b) ⋮ m
Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
a ⋮ m, b ⋮ m và c ⋮ m ⇒ (a + b + c) ⋮ m
- Tính chất 2: a :/. m và b ⋮ m ⇒ (a + b) :/. m
Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
a :/. m, b ⋮ m và c ⋮ m ⇒ (a + b + c) :/. m
- Dấu hiệu chia hết cho 2: Các số có chữ số tận cùng là chữ số chẵn thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
- Dấu hiệu chia hết cho 3: Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
- Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
- Dấu hiệu chia hết cho 9: Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Câu 48:
Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số y = sin2x + 2cos2x.
 Xem đáp án
Xem đáp án
Ta có: y = sin2x + 2cos2x = (sin2x + cos2x) + cos2x = 1 + cos2x
Do −1≤ cosx ≤ 1
Nên: 0 ≤ cos2x ≤ 1
Suy ra: 1 ≤ cos2x + 1 ≤ =2
Vậy GTLN của M là 2 khi cos2x = 1 ⇔ cosx = ±1 ⇔
GTNN của M là 1 khi cosx = 0 ⇔ .
Câu 49:
 Xem đáp án
Xem đáp án
Chia 6 cho lần lượt các số tự nhiên từ 1 đến 6.
6 chia hết cho 1; 2; 3; 6 nên Ư(6) = {1; 2; 3; 6}.
Tương tự như vậy Ư(9) = {1; 3; 9}
ƯC(6, 9) = Ư(6) ∩ Ư(9) = {1; 3}.
Câu 51:
Tìm các ước tự nhiên của 24.
 Xem đáp án
Xem đáp án
Các ước tự nhiên của 24 là: 1; 2; 3; 4; 6; 8; 12; 24.
Câu 52:
Tìm ước chung lớn nhất của 77 và 126.
 Xem đáp án
Xem đáp án
Ta có: 77 = 7.11; 126 = 2.32.7
ƯCLN(77, 126) = 7
Câu 53:
Bạn Kí đánh số trang sách bằng các số tự nhiên từ 1 đến 216. Bạn Kí phải viết tất cả bao nhiêu chữ số?
 Xem đáp án
Xem đáp án
Số chữ số để dùng đánh số trang từ 1 đến 9 là: (9 - 1) : 1 + 1 = 9 (chữ số).
Số chữ số để dánh số trang từ 10 đến 99 là: [(99 - 10) : 1 + 1] . 2 = 180 (chữ số).
Số chữ số để dánh số trang từ 100 đến 216 là : [(216 - 100) : 1 +1] . 3 = 351 (chữ số).
Từ 1 đến 216 là : 9 + 180 + 351 = 540 (chữ số).
Câu 54:
Từ ba tấm gỗ có độ dài 56 dm, 48 dm và 40 dm, bác thợ mộc muốn cắt thành các thanh gỗ có độ dài như nhau mà không để thừa mẩu gỗ nào. Hỏi bác cắt như thế nào để được các thanh gỗ có độ dài lớn nhất có thể?
 Xem đáp án
Xem đáp án
Độ dài lớn nhất của thanh gỗ chính là ƯCLN(56; 48; 40).
Mà ƯCLN(56; 48; 40) = 8 nên bác sẽ cắt thành các thanh gỗ có độ dài lớn nhất là 8 dm.
Câu 55:
Cho các mệnh đề P: “a và b chia hết cho c”;
Q: “a + b chia hết cho c”.
a) Hãy phát biểu định lý P ⇒ Q. Nêu giả thiết và kết luận của định lí và phát biểu định lí dưới dạng điều kiện cần, điều kiện đủ.
b) Hãy phát biểu mệnh đề đảo của mệnh đề P ⇒ Q rồi xác định tính đúng sai của mệnh đề đảo này.
 Xem đáp án
Xem đáp án
a) Định lí P ⇒ Q được phát biểu như sau:
Nếu a và b chia hết cho c thì a + b chia hết cho c.
Giả thiết của định lí là: a và b chia hết cho c;
Kết luận của định lí là: a + b chia hết cho c.
Định lý P ⇒ Q được phát biểu dưới dạng điều kiện cần và đủ là:
a và b chia hết cho c là điều kiện đủ để a + b chia hết cho c.
a + b chia hết cho c là điều kiện cần để a và b chia hết cho c.
b) Mệnh đề đảo của mệnh đề P ⇒ Q được phát biểu như sau:
Nếu a + b chia hết cho c thì a và b chia hết cho c.
Ví dụ: a = 10, b = 2, c = 3
Ta có: a + b = 10 + 2 = 12 chia hết cho 3 nhưng a = 10 không chia hết cho 3 và b = 2 cũng không chia hết cho 3. Do đó mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề sai.
Câu 56:
Từ các chữ số 3, 1, 7 hãy viết tất cả các số có ba chữ số, mỗi số có cả ba chữ số đó rồi xếp các số theo thứ tự từ bé đến lớn.
 Xem đáp án
Xem đáp án
Tất cả các số có 3 chữ số lập từ 3, 1, 7 là:
317, 371 ,173, 137 ,713, 731
Sắp xếp theo thứ tự từ bé đến lớn: 137, 173, 317, 371 ,713, 731.
Câu 57:
Từ bốn chữ số 3; 4; 5; 0 hãy ghép thành các số tự nhiên có 3 chữ số khác nhau thỏa mãn:
a) Chia hết cho 3;
b) Chia hết cho 3 nhưng không chia hết cho 9.
 Xem đáp án
Xem đáp án
a) Tìm bộ ba số có tổng chia hết cho 3, ta được: (3; 4; 5); (4; 5; 0). Từ đó ta có các số chia hết cho 3 là: 345; 354; 453; 435; 543; 534; 450; 405; 540; 504.
b) Tìm bộ ba số chia hết cho 3 nhưng không chia hết cho 9. Từ đó ta có các số thỏa mãn: 345; 354; 453; 435; 543; 534.
Câu 60:
Trong hộp có 45 quả bóng gồm 20 quả màu đỏ, 15 quả màu xanh và 10 quả màu vàng. Bạn lấy bao nhiêu quả bóng để chắc chắn có 3 quả bóng:
a. Màu đỏ.
b. Cùng màu.
c. Khác màu.
 Xem đáp án
Xem đáp án
a) 28 quả
Vì nếu ta lấy ra 15 quả màu xanh và 10 quả màu vàng tức là không có màu đỏ thì ta tiếp tục lấy 3 quả nữa mới được 3 quả màu đỏ.
Mà 15 + 10 + 3 = 28.
b) 5 quả
Lúc đầu chúng ta lấy một quả xanh và một quả đỏ thì chúng ta phải lấy ít nhất 2 quả xanh hoặc 2 quả đỏ hoặc 3 quả. Tương tự các trường hợp khác cũng vậy
c) 36 quả
Lúc đầu chúng ta lấy 20 quả màu đỏ, rồi lại lấy đúng 15 quả màu xanh thì chúng ta phải lấy thêm 1 quả màu xanh nữa thì mới có 3 quả khác màu.
Vậy lấy: 20 + 15 + 1 = 36 (quả).
Câu 61:
Trong ngày đại hội thể dục thể thao, số học sinh của một trường khi xếp thành 12 hàng, 18 hàng và 21 hàng đều thừa 1 học sinh. Hỏi trường đó có bao nhiêu học sinh? (Biết số học sinh trong khoảng từ 500 đến 600).
 Xem đáp án
Xem đáp án
Gọi x (học sinh) là số học sinh của trường (x ∈ ℕ*; 500 < x < 600).
Theo bài ra, số học sinh của một trường khi xếp thành 12 hàng, 18 hàng, 21 hàng đều thừa 1 học sinh nên x – 1 chia hết cho 12; 18; 21
Hay x – 1 là ƯC(12, 18, 21).
Ta có: 12 = 22.3; 18 = 2.32; 21 = 3.7.
BCNN(12, 18, 21) = 22.32.7 = 252
x – 1 = 252k (k ∈ ℕ*)
x = 252k +1
Mà 500 < x < 600
500 < 252k + 1 < 600
1,98 < k < 2,38
k = 2
Do đó x = 2.252 + 1
x = 505
Vậy số học sinh của trường là 505.
Câu 62:
Trung bình cộng của 10 số lẻ liên tiếp là 100. Tìm số lẻ lớn nhất trong 10 số lẻ đó.
 Xem đáp án
Xem đáp án
10 số lẻ liên tiếp lập thành 1 cấp số cộng với số hạng đầu là u1; công sai d = 2 vì các số lẻ liên tiếp hơn kém nhau 2 đơn vị
Số lẻ đầu tiên là u1; thì số lẻ thứ 10 là u1 + 9d
Tổng 10 số lẻ là: (u1 + u1 + 9d).10 : 2 = 100
⇔ (2u1 + 9.2) = 100.2 : 10
⇔ u1 = 1
Số lẻ lớn nhất là số lẻ cuối cùng, là số lẻ thứ 10
Số lẻ lớn nhất là: 1 + 9.2 = 19.
Câu 63:
Trường hợp nào sau đây chỉ tập hợp số tự nhiên?
A. {1; 2; 3; 4; …}.
B. {0; 1; 2; 3; 4; …}.
C. {0; 1; 2; 3; 4; …}.
D. {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
 Xem đáp án
Xem đáp án
Các số 0, 1, 2, 3, 4 … là các số tự nhiên.
Tập hợp các số tự nhiên được kí hiệu là ℕ, tức là ℕ = {0; 1; 2; 3; 4; …}.
Chọn đáp án B.
Câu 64:
Trục số là gì? Trục số dùng để làm gì?
 Xem đáp án
Xem đáp án
Trục số là một đường thẳng có các số nguyên âm được biểu diễn trên tia đối của tia số và có các số −1; −2; −3; ...; -1; -2; -3; ...
Dùng để:
- Tính toán phép tính gần cộng trừ đơn giản
- Tính số âm
- Đôi khi biểu diễn nhiệt độ
Ví dụ hình ảnh trục số:

Câu 65:
Trong không gian cho đường thẳng a chứa trong mặt phẳng (P) và đường thẳng b song song với mặt phẳng (P) . Mệnh đề nào sau đây là đúng?
A. a // b.
B. a, b không có điểm chung.
C. a, b cắt nhau.
D. a, b chéo nhau.
 Xem đáp án
Xem đáp án
Vì a ⊂ (P) và b//(P) nên a, b không có điểm chung.
Chỉ có thể suy ra a, b chéo nhau.
Chưa thể kết luận được a//b.
Nếu kết luận a//b sẽ sai vì b//(P) thì b // c ⊂ (P) nên chưa chắc b // a
Chọn D.
Câu 67:
Trong 1 lớp học có 40 học sinh trong đó có 30 học sinh đạt học sinh giỏi môn toán 25 học sinh đạt học sinh giỏi môn văn biết rằng chỉ có 5 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả 2 môn toán và văn hỏi có bao nhiêu học sinh chỉ học giỏi 1 trong 2 môn toán hoặc văn.
 Xem đáp án
Xem đáp án
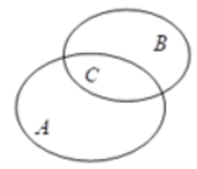
Gọi A là tập hợp các học sinh đạt học sinh giỏi môn Toán.
B là tập hợp các học sinh đạt học sinh giỏi môn Văn.
C là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
Số học sinh đạt học sinh giỏi môn Toán, Văn của lớp là: 40 – 5 = 35 (học sinh).
Theo sơ đồ Ven ta có: A + B – C = 35. ⇔ 30 + 25 – C = 35 ⇔ C = 20.
Do vậy ta có:
Số học sinh chỉ giỏi môn Toán là: A – C = 30 – 20 = 10 (học sinh).
Số học sinh chỉ giỏi môn Văn là: B – C = 25 – 20 = 5 (học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là: 10 + 5 = 15 (học sinh).
Câu 68:
Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.
 Xem đáp án
Xem đáp án
Tổng quát: a = b . q + r (0 ≤ r < b)
Gọi số chia và thương lần lượt là: b, q
Ta có: 200 = b . q + 13 (r ≠ 0)
⇒ 200 - 13 = b . q
⇒ 187 = b . q
Ta có: 187 = 1. 187 = 17 . 11
Mà số dư bao giờ nhỏ hơn số chia
⇒ Số chia là 17 và thương là 11.
Câu 69:
Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.
 Xem đáp án
Xem đáp án
Tổng quát: a = b . q + r (0 ≤ r < b)
Gọi số chia và thương lần lượt là: b, q
Ta có: 200 = b . q + 13 (r ≠ 0)
⇒ 200 - 13 = b . q
⇒ 187 = b . q
Ta có: 187 = 1. 187 = 17 . 11
Mà số dư bao giờ nhỏ hơn số chia
⇒ Số chia là 17 và thương là 11.
Câu 70:
Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.
 Xem đáp án
Xem đáp án
Tổng quát: a = b . q + r (0 ≤ r < b)
Gọi số chia và thương lần lượt là: b, q
Ta có: 200 = b . q + 13 (r ≠ 0)
⇒ 200 - 13 = b . q
⇒ 187 = b . q
Ta có: 187 = 1. 187 = 17 . 11
Mà số dư bao giờ nhỏ hơn số chia
⇒ Số chia là 17 và thương là 11.
Câu 71:
Chứng minh rằng trong n + 1 số bất kỳ thuộc tập hợp {1; 2; 3; …; 2n} luôn chọn được 2 số mà số này là bội của số kia.
 Xem đáp án
Xem đáp án
Viết n + 1 số đã cho dưới dạng : ![]()
Trong đó b1,b2,...,bn+1 là các số lẻ.
Ta có: 1 ≤ b1,b2,...,bn+1 ≤ 2n – 1
Mà trong khoảng từ 1 đến 2n – 1 có n số lẻ nên tồn tại 2 số p khác q sao cho bp = bq
Khi đó ap và aq có 1 số là bội của số kia.
Vậy trong n + 1 số bất kỳ thuộc tập hợp {1; 2; 3; …; 2n} luôn chọn được 2 số mà số này là bội của số kia.
Câu 72:
Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn 40 học sinh lớp 11 của trường THPT X thực hiện kế hoạch quyên góp như sau: Ngày đầu tiên mỗi bạn quyên góp 2000đ, từ ngày thứ hai trở đi mỗi bạn quyên góp hơn ngày liền trước là 500đ. Hỏi sau bao nhiêu ngày thì số tiền quyên góp được là 9800000đ.
 Xem đáp án
Xem đáp án
Số tiền mà học sinh lớp 11 trường X quyên góp vào ngày đầu tiên là:
2000.40 = 80000 (đồng)
Vì cứ mỗi ngày mỗi bạn đều quyên góp hơn ngày trước là 500 đồng nên chênh lệch giữa số tiền quyên góp giữa ngày đầu tiên và ngày thứ hai là 500.40 = 20000 đồng.
Xem số tiền quyên góp của học sinh lớp 11 trường X là một cấp số cộng với:
u1 = 8 + 2d (nghìn đồng)
Lúc này ta có số tiền mà các bạn quyên góp được sau n ngày là:
⇔ 2n2 + 14n – 1960 = 0
⇔ (2n – 56)(n + 35) = 0
⇔
Vậy sau 28 ngày thì 40 học sinh quyên góp đủ số tiền 9,8 triệu đồng.
Câu 73:
Trong 1 hội nghị có 100 đại biểu tham dự, mỗi đại biểu nói được một hoặc hai trong ba thứ tiếng: Nga, Anh hoặc Pháp. Có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?
 Xem đáp án
Xem đáp án
Số đại biểu nói được tiếng Pháp hoặc tiếng Nga là:
100 - 39 = 61 (đại biểu)
Số đại biểu nói được tiếng Nga mà lại không nói được tiếng Pháp là:
61 - 35 = 26 (đại biểu)
Số đại biểu chỉ nói được tiếng Nga là:
26 - 8 = 18 (đại biểu)
Đáp số: 18 đại biểu.
Câu 74:
Một lô hàng có 10 sản phẩm, trong đó có 8 chính phẩm và 2 phế phẩm. Lấy tùy ý 6 sản phẩm từ lô hàng đó. Xét biến cố D: “Lấy 6 sản phẩm từ lô hàng và không có quá một phế phẩm”. Số kết quả thuận lợi của biến cố D là?
 Xem đáp án
Xem đáp án
Cách 1:
Trường hợp 1: Lấy 6 sản phẩm từ lô hàng và không có phế phẩm nào.
Chọn 6 sản phẩm trong đó không có phế phẩm tức là 6 chính phẩm trong 8 chính phẩm của lô hàng và không tính đến thứ tự có (cách chọn).
Trường hợp 2: Lấy 6 sản phẩm từ lô hàng và có 1 phế phẩm.
⦁ Số cách chọn 1 phế phẩm trong 2 phế phẩm là: (cách chọn).
⦁ Số cách chọn 5 sản phẩm còn lại trong 8 chính phẩm của lô hàng và không tính đến thứ tự là: (cách chọn).
Theo quy tắc nhân, ta có tất cả cách chọn 6 sản phẩm từ lô hàng, trong đó có 1 phế phẩm.
Trong cả hai trường hợp, ta có số kết quả thuận lợi cho biến cố A là:
Vậy số kết quả thuận lợi cho biến cố A là 140.
Do đó ta chọn phương án C.
Cách 2:
Lấy 6 sản phẩm từ lô hàng có 10 sản phẩm nên tổng số kết quả có thể xảy ra là .
Xét biến cố B: “Lấy 6 sản phẩm từ lô hàng và có 2 phế phẩm”.
• Số cách chọn 2 phế phẩm trong 2 phế phẩm là: (cách chọn).
⦁ Số cách chọn 4 sản phẩm còn lại trong lô hàng và không tính đến thứ tự là: (cách chọn).
Theo quy tắc nhân, ta có tất cả cách chọn 6 sản phẩm từ lô hàng, trong đó có 2 phế phẩm.
Số kết quả thuận lợi cho biến cố B là
Vậy số kết quả thuận lợi cho biến cố A là .
Câu 75:
Chứng tỏ rằng: Trong ba số tự nhiên liên tiếp, có một số chia hết cho 3.
 Xem đáp án
Xem đáp án
Gọi ba số tự nhiên liên tiếp là a, a + 1, a + 2
Nếu a chia hết cho 3 thì bài toán được chứng minh
Nếu a không chia hết cho 3 thì a = 3k + 1 hoặc a = 3k + 2 (k ∈ N)
Nếu a = 3k + 1 thì a + 2 = 3k + 1 + 2 = 3k + 3 ⋮ 3
(vì 3k ⋮ 3 và 3 ⋮ 3 nên 3k + 3 ⋮ 3)
Nếu a = 3k + 2 thì a + 1 = 3k + 2 + 1 = 3k + 3 ⋮ 3
(vì 3k ⋮ 3 và 3 ⋮ 3 nên 3k + 3 ⋮ 3)
Vậy trong ba số tự nhiên liên tiếp, có một số chia hết cho 3.
Câu 76:
Trong buổi học kỹ năng sống ở Sóc Sơn, các bạn lớp 7A đã được hướng dẫn cách dựng lều chữ A (dạng hình lăng trụ đứng có đáy là tam giác đều) từ một tấm vải bạt cho trước.
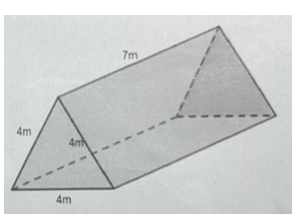
a) Tính diện tích vải bạt cần sử dụng để làm hai mái và trải đáy của lều, biết kích thước lều như trên hình vẽ.
 Xem đáp án
Xem đáp án
a) Diện tích xung quanh hình lăng trụ chính là diện tích vải bạt cần sử dụng (vì đề chỉ yêu cầu vải bạt sử dụng làm 2 mái và trải đáy nên ta không tính diện tích 2 mặt đáy)
Chu vi tam giác đáy là: 4.3 = 12 (m)
Diện tích xung quanh hình lăng trụ hay diện tích vải bạt là:
12.7 = 84 (m2)
Câu 77:
b) Nếu giáo viên lớp chuẩn bị được tấm vải bạt dài 15m rộng 7m thì tấm vải bạt cần thêm diện tích là bao nhiêu đủ để làm hai mái và trải đáy của lều?
 Xem đáp án
Xem đáp án
b) Diện tích vải bạt giáo viên chuẩn bị là:
15.7 = 105 (m2)
Vậy diện tích tấm bạt đã đủ để làm hai mái và trải đáy.
Câu 78:
Trong các hàm số sau hàm số nào là hàm số chẵn:
A. y = sin2x.
B. y = cos3x.
C. y = cot4x.
D. y = tan5x.
 Xem đáp án
Xem đáp án
Chọn B
Xét hàm số y = f(x) = cos3x
TXĐ: D = ℝ
Với mọi x ∈ ℝ ta có – x ∈ ℝ và f(-x) = cos(3(-x)) = cos3x = f(x)
Nên y = cos3x là hàm số chẵn trên ℝ
Câu 79:
Trong các hàm số sau hàm số nào là hàm số chẵn:
A. y = -sinx.
B. y = cosx – sinx.
C. y = cosx + sin2x.
D. y = cosx.sinx.
 Xem đáp án
Xem đáp án
Chọn đáp án C
Tất các các hàm số đều có TXĐ: D = R
Do đó ∀x ∈ D ⇒ − x ∈ D.
Bây giờ ta kiểm tra f(x) = f(-x) hoặc f(-x) = - f(x).
· Với y = f(x) = - sinx.
Ta có f(-x)= - sin (-x) = sinx = - (- sinx) ⇒ f(−x)=−f(x)
Suy ra hàm số y = -sinx là hàm số lẻ.
· Với y = f(x) = cosx –sinx.
Ta có f(−x) = cos(−x) − sin(−x) = cosx + sinx ⇒ f(−x) ≠ −f(x) và f(x)
Suy ra hàm số y = cosx - sinx không chẵn không lẻ.
· Với y = f(x) = cosx + sin2x
Ta có f(−x) = cos(−x) + sin2(−x) = cos(−x) + [sin(−x)]2 = cosx+[−sinx]2 = cosx + sin2x
⇒ f(−x) = f(x)
Suy ra hàm số y = cosx + sin2x là hàm số chẵn.
· Với y = f(x) = cosxsinx.
Ta có f(−x) = cos(−x).sin(−x) = −cosxsinx
⇒ f(−x) = −f(x)
Suy ra hàm số y = cosxsinx là hàm số lẻ.
Câu 80:
Trong các phát biểu sau, phát biểu nào về khối tròn xoay là không đúng?
A. Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được hình cầu.
B. Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình trụ.
C. Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được hình tròn.
D. Khi quay hình tam giác vuông một vòng quanh một góc vuông cố định, ta được hình nón.
 Xem đáp án
Xem đáp án
Chọn đáp án D.
Khi quay nửa hình tròn một vòng quanh đường kính cố định, ta được hình tròn.
Câu 81:
Trong một phép chia có số bị chia là 200, số dư là 13. Tìm số chia và số bị chia.
 Xem đáp án
Xem đáp án
Tổng quát: a = b . q + r (0 ≤ r < b)
Gọi số chia và thương lần lượt là: b, q
Ta có: 200 = b . q + 13 (r ≠ 0)
⇒ 200 - 13 = b . q
⇒ 187 = b . q
Ta có: 187 = 1. 187 = 17 . 11
Mà số dư bao giờ nhỏ hơn số chia
⇒ Số chia là 17 và thương là 11.
Câu 82:
Trong hộp có 100 viên bi,an và nam chơi trò chơi như sau mỗi lần chơi được bốc k viên bi ( 0 < k < 11). Người bốc bi ở lượt chơi cuối cùng là người thắng cuộc. Chứng minh rằng ai đi trước là người có chiến thuật để dành chiến thắng
 Xem đáp án
Xem đáp án
Ta thấy để người nào đó muốn thắng cuộc thì người đó phải làm sao bốc được viên bi cuối cùng. Suy ra đến lượt người đó lần cuối phải còn 1, 2, … hoặc 10 viên bi.
Như vậy, cứ khi nào còn lại 1, 2, … hoặc 10 viên bi và đến lượt người nào đó chơi thì người đó sẽ thắng.
Vì mỗi lượt bốc ít nhất 1 viên bi và nhiều nhất 10 viên bi, lần lượt mỗi người bốc nên người đi sau luôn có thể bốc để "kiểm soát" sao cho số bi của hai người bốc sau mỗi lượt là bằng 11. Thật vậy nếu người trước bốc 1 thì người sau bốc 10, người trước bốc 2 thì người sau bốc 9,… người trước bốc 9 thì người sau bốc 1.
Giả sử An bốc trước, An sẽ thực hiện bốc như sau:
- Lần 1 An bốc 1 viên, còn lại 99 viên.
- Lúc này đến lượt Nam bốc, Nam bốc bao nhiêu viên thì tiếp theo An bốc bù vào để được hai người bốc 11 viên trong 2 lượt liên tiếp.
Khi đó sau: 99 : 11 = 9 lần nữa thì An sẽ là người bốc cuối cùng, và An thắng cuộc.
Câu 84:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx + 5. Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P):y = x2 tại hai điểm phân biệt có hoành độ lần lượt là x1, x2 với x1 < x2) sao cho |x1| > |x2|.
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của (d) và (P):
x2 = mx + 5
⇔ x2 – mx – 5 = 0
Ta có tích hệ số ac = −5 < 0 nên phương trình hoành độ giao điểm luôn có 2 nghiệm phân biệt với mọi m hay thẳng (d) cắt parabol (P) tại hai điểm phân biệt với mọi m.
Theo hệ thức Vi-ét ta có:
Ta có: |x1| > |x2| ⇔ x12 > x22
⇔ x12 - x22 > 0
⇔ (x1 - x2)(x1 + x2) > 0
Theo giả thiết x1 < x2 nên x1 – x2 < 0
Do đó: x1 + x2 < 0
Hay m < 0
Vậy m < 0.
Câu 85:
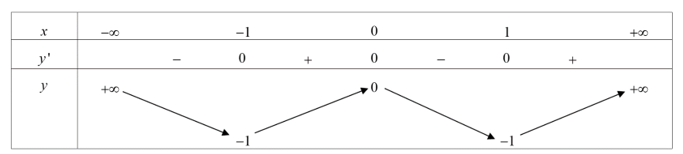
Cho hàm số y = f(x) xác định, liên tục trên Rℝ và có bảng biến thiên sau
Tìm tất cả các giá trị thực của tham số m để phương ctrình f(x) = m vô nghiệm.
 Xem đáp án
Xem đáp án
Ta có : f(x) = m
Dựa vào bảng biến thiên: phương trình vô nghiệm khi: m < -1
Vậy m < -1 thì f(x) = m vô nghiệm.
Câu 87:
Tìm 3 số thập phân x thỏa mãn 35,82 < x < 35,83.
 Xem đáp án
Xem đáp án
35,82 < x < 35,83
x có thể là 35,821; 35,822; 35,823.
Câu 88:
Tổng của hai số là 407 . Biết của số thứ 1 thì bằng của số thứ 2. Tìm 2 số đó.
 Xem đáp án
Xem đáp án
Gọi số thứ 1 là a, số thứ 2 là b
Ta có:
Vậy số thứ nhất là 148, số thứ hai là 259.
Câu 89:
Tính nhanh S = 1 + 4 + 7 + ... + 2008.
 Xem đáp án
Xem đáp án
S = 1 + 4 + 7 + ... + 2008
Mỗi số hạng cách nhau 3 đơn vị
Số số hạng của dãy S là: (2008 – 1) : 3 + 1 = 670
Tổng S = (2008 + 1).670 : 2 = 673015.
Câu 90:
Cho hai tập hợp A = [m - 4; 1], B = (-3; m]. Tính tổng tất cả các giá trị nguyên của m để A ∪ B = B.
 Xem đáp án
Xem đáp án
Để tập hợp A và tập hợp B có nghĩa thì
A ∪ B = B suy ra A ⊂ B
Suy ra:
Vậy 1 < m ≤ 5
Nên m ∈ {2; 3; 4; 5}
Tổng các giá trị của m = 2 + 3 + 4 + 5 = 14.
Câu 91:
Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.
 Xem đáp án
Xem đáp án
Nhận thấy M, N là 2 đoạn cùng có độ dài bằng 6, nên để M ∪ N là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
+) 2m – 1 ≤ m + 1 ≤ 2m + 5 ⟺ m ∈ [−4; 2] (1)
Khi đó: M ∪ N = [2m − 1; m + 7] nên M ∪ N là 1 đoạn có độ dài bằng 10 khi:
(m + 7) − (2m − 1) = 10
⇔ m = −2 (TM (1))
+) 2m – 1 ≤ m + 7 ≤ 2m + 5
⟺ m ∈ [2; 8] (2)
Khi đó: M ∪ N = [m + 1; 2m + 5] nên M ∪ N là 1 đoạn có độ dài bằng 10 khi:
(2m + 5) − (m + 1) = 10
⇔ m = 6 (TM (2))
Vậy tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10 là –2 + 6 = 4.
Câu 92:
Tính tổng tất cả các số có ba chữ số khác nhau mà các chữ số đều lẻ.
 Xem đáp án
Xem đáp án
Các chữ số đều lẻ được viết từ các số: 1, 3, 5, 7, 9 vì các số có 3 chữ số khác nhau nên ta có: hàng trăm có 5, hàng chục còn 4 cách chọn, hàng đơn vị còn 3 cách chọn
⇒ số các số có 3 chữ số khác nhau mà các chữ số đều lẻ là: 5.4.3 = 60 (số)
Từ hàng trăm, hàng chục, hàng đơn vị, mổi chữ số từ các số 1, 3, 5, 7, 9 xuất hiện:
60 : 5 = 12 (lần)
⇒ Tổng tất cả các số có 3 chữ số khác nhau mà các chữ số đều lẻ là:
12.(1 + 3 + 5 + 7 + 9).100 + 12.(1 + 3 + 5 + 7 + 9).10 + 12(1 + 3 + 5 + 7 + 9)
= 12.25.100 + 12.25.10 + 12.25
= 30000 + 3000 + 300
= 33300.
Câu 93:
Một hộp có 5 viên bi đỏ, 4 viên bi trắng. Chọn ngẫu nhiên 2 viên bi. Xác suất 2 viên bi được chọn có đủ hai màu là?
 Xem đáp án
Xem đáp án
Số phần tử không gian mẫu: n(Ω) =
(vì có 9 viên bi chọn ngẫu nhiên ra 2 viên bi).
Gọi A là biến cố: “hai viên bi được chọn có đủ hai màu”.
Vì chọn ngẫu nhiên 2 viên bi có đủ hai màu nên ta chọn chọn 1 bi đen từ 5 bi đen, chọn 1 bi trắng từ 4 bi trắng.
Khi đó số phần tử của biến cố A là n(A)
Xác suất của biến cố A là: .