- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 95)
-
12966 lượt thi
-
91 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Một cửa hàng ngày thứ nhất bán được 102 tạ gạo và nhiều hơn ngày thứ hai 7 tạ gạo nhưng lại ít hơn ngày thứ ba 15 tạ gạo. Hỏi cả ba ngày cửa hàng bán được bao nhiêu gạo?
 Xem đáp án
Xem đáp án
Ngày thứ 2 bán được:
102 – 7 = 95 (tạ)
Ngày thứ 3 bán được:
102 + 15 = 117 (tạ)
Cả 3 ngày bán được:
102 + 95 + 117 = 314 (tạ)
Đáp số: 314 tạ.
Câu 2:
1 cửa hàng trong 3 ngày bán được có 2 tấn đường. Ngày đầu bán được 800 kg. Ngày thứ hai bán được bằng số đường bán được ngày ban đầu . Hỏi ngày thứ ba bán được bao nhiêu kg đường?
 Xem đáp án
Xem đáp án
Đổi 2 tấn = 2000kg
Ngày thứ hai bán được là:
800 . 4 : 5 = 640 (kg)
Ngày thứ ba bán được là:
2000 – 800 – 640 = 560 (kg)
Đáp số: 560 kg đường.
Câu 3:
Một cuốn sách được đánh số trang từ 3 và có 120 trang. Hỏi phải dùng bao nhiêu số 1 để đánh số trang cuốn sách đó?
 Xem đáp án
Xem đáp án
Những trang có chữ số 1 ở hàng trăm: 100; 101; 102; 103; …; 120.
⇒ Có: (120 - 100).1 + 1 = 3 (chữ số 1)
Những trang có chữ số 1 ở hàng chục: 10; 11; 12; …; 19; 110; 111; 112; …; 119.
⇒ Có 10 + 10 = 20 (chữ số 1)
Những trang có chữ số 1 ở hàng đơn vị: 11; 21; …111.
⇒ Có (111 – 11) : 10 + 1 = 11 (chữ số 1).
Phải dùng tất cả: 21 + 20 + 11 = 52 (chữ số 1).
Câu 4:
Một ô tô đi 54 km cần có 6 lít xăng. Hỏi ô tô đó đi hết quãng đường dài 216 km thì cần có bao nhiêu lít xăng?
 Xem đáp án
Xem đáp án
216km gấp 54km số lần là:
216 : 54 = 4 (lần)
Số lít xăng cần có để ô tô đi hết quãng đường dài 216km là:
6 . 4 = 24 (lít)
Đáp số: 24 lít xăng.
Câu 5:
Một đội 12 người làm xong một cái khối trong 10 ngày hỏi muốn làm xong công việc đó trong 8 ngày thì cần bao nhiêu công nhân?
 Xem đáp án
Xem đáp án
1 người làm được trong số ngày là:
12.10 = 120 (ngày)
Trong 8 ngày thì cần số công nhân là:
120 : 8 = 15 (công nhân)
Đáp số: 15 công nhân.
Câu 6:
 Xem đáp án
Xem đáp án
Sau 2 tuần lễ đầu thì đội công nhân cần sửa thêm số % là:
100% - 40 % - 30 %= 30%
Tuần lễ thứ ba sửa được số % quãng đường là:
50% : 2 = 25%
Tuần thứ tư sửa được số % quãng đường là:
100% - 25 % - 40% - 30% = 5%
Đổi 4km 200m = 4200 m
Đội đó đã sửa được quãng đường dài số m là:
4200 : 5 . 100 = 84000(m)
Đổi 84000m = 84 km.
Đáp số: 84 km.
Câu 7:
Một đội công nhân có 77 người nhận sửa xong một quãng đường trong 9 ngày. Hỏi muốn làm xong quãng đường đó trong 7 ngày thì cần thêm bao nhiêu người ? (mức làm của mỗi người như nhau).
 Xem đáp án
Xem đáp án
Nếu muốn sửa xong quãng đường trong 1 ngày thì cần số người là:
77 . 9 = 693 (người)
Muốn làm xong quảng đường đó trong 7 ngày thì số người là:
693 : 7 = 99 (người)
Cần thêm số người là:
99 – 77 = 22 (người)
Đáp số: 22 người.
Câu 8:
Một đội sinh viên tình nguyện có 54 nam và 45 nữ. Có thể chia đội nhiều nhất thành mấy tổ để được số nam và nữ chia đều cho các tổ?
 Xem đáp án
Xem đáp án
Gọi số tổ có thể chia được là x (x > 1)
Vì số nam nữ được chia đều vào các tổ nên 54 ⋮ x; 45 ⋮ x
Hay x ∈ ƯCLN(54, 45)
Mà: 54 = 2.33; 45 = 5.32
Nên ƯCLN(54, 45) = 32 = 9
Vậy có thể chia đội nhiều nhất thành 9 tổ
Khi đó mỗi tổ sẽ có: 6 nam (54 : 9 = 6) và 5 nữ (45 : 9 = 5).
Câu 10:
1 giá sách có 2 ngăn, ngăn A và ngăn B. Số sách ngăn A bằng số sách ngăn B. Nếu chuyển 3 quyển từ A sang ngăn B thì số sách ngăn A bằng số sách ngăn B. Tính tổng số sách 2 ngăn?
 Xem đáp án
Xem đáp án
Gọi số sách ngăn A và ngăn B lần lượt là a, b:
Theo đề, ta có:
Vậy ngăn A có 12 quyển; ngăn B có 18 quyển.
Tổng số sách của 2 ngăn là: 12 + 18 = 30 (quyển).
Câu 11:
Một hình chóp có tất cả 2022 cạnh thì số đỉnh là?
 Xem đáp án
Xem đáp án
Một hình chóp có tất cả 2022 cạnh tức là hình chóp có đáy có: cạnh.
Tức là đáy có 1011 điểm ở đáy
Kết hợp với 1 đỉnh
Vậy hình chóp có: 1011 + 1 = 1012 (đỉnh).
Câu 12:
Một hình chữ nhật có chiều dài bằng 16cm; diện tích bằng a. Tính chiều rộng của hình chữ nhật (là một số tự nhiên) nếu biết a là một số tự nhiên từ 220 đến 228.
 Xem đáp án
Xem đáp án
Giả sử chiều rộng của hình chữ nhật là b (cm, b > 0).
Diện tích của hình chữ nhật là: a = 16. b
Mà theo bài toán a là một số tự nhiên từ 220 đến 228 nên hay . Do đó:
Phép chia 220: 16 = 13 (dư 12)
Phép chia 228: 16 = 14 (dư 4)
Vì nên suy ra b = 14 cm.
Vậy chiều rộng của hình chữ nhật là 14cm.
Câu 13:
Một kho hàng cần đến 70 xe ô tô vận chuyển liên tục trong 30 ngày mới hết. Sau khi vận chuyển được 6 ngày thì 10 xe phải sửa chữa. Hỏi số xe còn lại phải vận chuyển hết số hàng còn lại trong bao nhiêu ngày. Biết sức vận chuyển của mỗi xe trong một ngày là như nhau.
 Xem đáp án
Xem đáp án
30 ngày chở hết số hàng:
70.30 = 2100 (hàng)
6 ngày chở hết số hàng:
70.6 = 420 (hàng)
Số hàng còn lại:
2100 – 420 = 1680 (hàng)
Số hàng còn lại chở trong số ngày:
1680 : (70 - 10) = 28 (ngày)
Số xe còn lại phải vận chuyển hết số hàng còn lại trong bao có số ngày:
28 - (30 - 4) = 4 (ngày)
Đáp số: 4 ngày.
Câu 14:
Một khu vườn hình chữ nhật có chiều dài 15m và chiều rộng 8m. Người ta muốn làm hàng rào xung quanh vườn bằng lưới sắt và đề cổng ra vào rộng 2m. Biết chiều cao của lưới sắt là 1m và giá mỗi m2 lưới sắt là 20 000 đồng. Hỏi người ta phải chi phí bao nhiêu tiền để mua lưới sắt?
 Xem đáp án
Xem đáp án
Chu vi khu vườn là:
(15 + 8).2 = 46 (m)
Hàng rào dài số mét là:
46 – 2 = 44 (m)
Diện tích hàng rào là:
44.1 = 44 (m2)
Tổng chi phí mua lưới sắt là:
44 . 20000 = 880000 (đồng).
Câu 15:
Một khu vườn hình chữ nhật có chu vi 140m, chiều rộng bằng chiều dài. Tính diện tích của khu vườn hình chữ nhật đó?
 Xem đáp án
Xem đáp án
Nửa chu vi của khu vườn hình chữ nhật là:
140 : 2 = 70 (m)
Ta có sơ đồ sau:
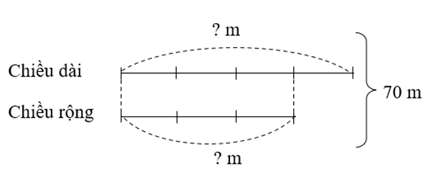
Theo sơ đồ, tổng số phần bằng nhau là:
3 + 4 = 7 (phần)
Chiều rộng của khu vườn là:
70 : 7 × 3 = 30 (m)
Chiều dài của khu vườn là:
70 – 30 = 40 (m)
Diện tích của khu vườn là:
30 × 40 = 1200 (m2)
Đáp số: 1200 m2.
Câu 16:
Một mảnh đất hình chữ nhật có chiều dài 8m chiều rộng 6m. Người ta xây lối đi xung quanh mảnh đất 1m phần còn lại để trồng rau. Tính chu vi và diện tích mảnh vườn. Tính diện tích trồng rau và diện tích để làm lối đi.
 Xem đáp án
Xem đáp án
Diện tích mảnh đất là:
8.6 = 48 (m2)
Diện tích lối đi là:
1.8 = 8 (m2)
Diện tích trồng rau là:
48 – 8 = 40 (m2).
Câu 17:
Một hộ được chia một diện tích đất nhất định nếu lấy mảnh hình chữ nhật rộng 3m thì chiều dài là 14m hỏi nếu hộ gia đình đó lấy mảnh đất hình chữ nhật rộng 6m thì chiều dài là bao nhiêu mét?
 Xem đáp án
Xem đáp án
Diện tích mảnh đất được chia là:
14 . 3 = 42 (m²)
Chiều dài mảnh đất nếu chiều rộng là 6m là:
42 : 6 = 7 (m)
Đáp số: 7m.
Câu 18:
Một học sinh đặt kế hoạch cho mình tháng này phải đạt tổng số 180 điểm. Do cố gắng bạn đó đã đạt được 207 điểm. Hỏi:
a) Bạn đó đạt bao nhiêu phần trăm kế hoạch.
 Xem đáp án
Xem đáp án
a) Bạn đó đạt số phần trăm kế hoạch là:
207 : 180 = 1,15 = 115%
Câu 19:
b) Bạn đó vượt mức bao nhiêu phần trăm so với kế hoạch.
 Xem đáp án
Xem đáp án
b) Bạn đó vượt mức số phần trăm so với kế hoạch là:
115 - 100 = 15 %.
Câu 20:
Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc X và Y để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại X là 250 nghìn đồng, giá một bao loại Y là 200 nghìn đồng. Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc X và Y sao cho hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C.
A. 1,95 triệu đồng.
B. 4,5 triệu đồng.
C. 1,85 triệu đồng.
D. 1,7 triệu đồng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi số bao loại X và số bao loại Y lần lượt là x bao và y bao (x, y ∈ ℕ).
Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C nên x bao loại X chứa 2x đơn vị chất dinh dưỡng A, 2x đơn vị chất dinh dưỡng B và 2x đơn vị chất dinh dưỡng C.
Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C nên y bao loại Y chứa y đơn vị chất dinh dưỡng A, 9y đơn vị chất dinh dưỡng B và 3y đơn vị chất dinh dưỡng C.
Hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C nên 2x + y ≥ 12; 2x + 9y ≥ 36; 2x + 3y ≥ 24.
Khi đó ta có hệ bất phương trình sau:
F(x; y) = 250x + 200y (triệu đồng).
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(5; 5) ∉ d1 và thay vào biểu thức x ta được 5 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(5; 5).
• Đường thẳng d2: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(5; 5) ∉ d2 và thay vào biểu thức y ta được 5 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d2 chứa điểm I(5; 5).
• Vẽ đường thẳng d3: 2x + y = 12 bằng cách vẽ đường thẳng đi qua hai điểm (6; 0) và (5; 2).
Chọn điểm I(5; 5) ∉ d3 và thay vào biểu thức 2x + y ta được 2 . 5 + 5 = 15 > 12.
Suy ra miền nghiệm của bất phương trình 2x + y ≥ 12 là nửa mặt phẳng bờ d3 chứa điểm I(5; 5).
• Vẽ đường thẳng d4: 2x + 9y = 36 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4,5; 3).
Chọn điểm I(5; 5) ∉ d4 và thay vào biểu thức 2x + 9y ta được 2 . 5 + 9 . 5 = 55 > 36.
Suy ra miền nghiệm của bất phương trình 2x + 9y ≥ 36 là nửa mặt phẳng bờ d4 chứa điểm I(5; 5).
• Vẽ đường thẳng d5: 2x + 3y = 24 bằng cách vẽ đường thẳng đi qua hai điểm (3; 6) và (6; 4).
Chọn điểm I(5; 5) ∉ d5 và thay vào biểu thức 2x + 3y ta được 2 . 5 + 3 . 5 = 25 > 24.
Suy ra miền nghiệm của bất phương trình 2x + 3y ≥ 24 là nửa mặt phẳng bờ d5 chứa điểm I(5; 5).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
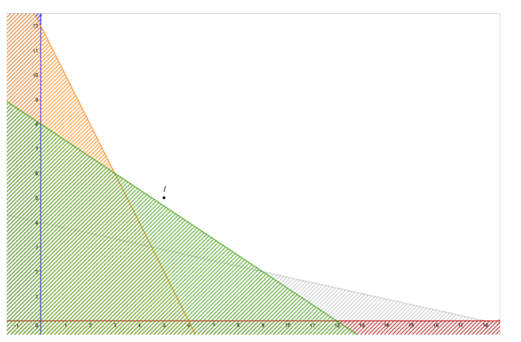
Miền nghiệm của hệ được giới hạn bởi các điểm (0; 12); (3; 6); (9; 2); (18; 0).
Ta có:
F(0; 12) = 250 . 0 + 200 . 12 = 2 400;
F(3; 6) = 250 . 3 + 200 . 6 = 1 950;
F(9; 2) = 250 . 9 + 200 . 2 = 2 650;
F(18; 0) = 250 . 18 + 200 . 0 = 4 500.
Khi đó ta thấy F(x; y) đạt giá trị nhỏ nhất bằng 1 950 tại x = 3; y = 6.
Vậy chi phí nhỏ nhất để mua hai loại thức ăn là 1,95 triệu đồng.
Câu 21:
Một lớp học có 25 học sinh chơi bóng đá; 23 học sinh chơi bóng bàn; 14 học sinh chơi bóng đá và bóng bàn và 6 học sinh không chơi môn nào cả. Số học sinh của cả lớp là?
 Xem đáp án
Xem đáp án

Số học sinh chỉ chơi bóng đá là: 25 – 14 = 11 (học sinh)
Số học sinh chỉ chơi bóng bàn là: 23 – 14 = 9 (học sinh)
Số học sinh của cả lớp là: 11 + 9 +14 + 6 = 40 (học sinh).
Câu 22:
Một lớp học có 28 nam và 24 nữ. Có bao nhiêu cách chia đều số học sinh vào các tổ với số tổ nhiều hơn sao cho số nam trong các tổ bằng nhau và số nữ trong các tổ bằng nhau? Cách chia nào để mỗi tổ có ít học sinh nhất?
 Xem đáp án
Xem đáp án
Gọi số tổ chia được nhiều nhất là x (x là số tự nhiên)
Chia 28 học sinh nữ vào x tổ nên 28 chia hết cho x
Chia 24 học sinh nam vào x tổ nên 24 chia hết cho x
Suy ra x là ước chung của 24 và 28
Mà số tổ chia được là lớn nhất nên x = ƯCLN(24, 28)
Ta có: 24 = 23.3; 28 = 22.7
⇒ ƯCLN(24, 28) = 22 = 4
Suy ra: x ∈ Ư(4) = {1; 2; 4}
Để mỗi tổ có ít học sinh nhất thì x lớn nhất. Nên x = 4.
Vậy có thể chia được nhiều nhất thành 4 tổ.
Khi đó mỗi tổ có 7 học sinh nữ và 6 học sinh nam.
Câu 24:
Một mảnh đất hình chữ nhật có chu vi 96 m, chiều dài bằng chiều rộng. Người ta đã sử dụng diện tích mảnh đất để xây nhà. Tính diện tích phần đất xây nhà.
 Xem đáp án
Xem đáp án
Nửa chu vi của mảnh đất là: 96 : 2 = 48 (m).
Tổng số phần bằng nhau là: 5 + 3 = 8 (phần)
Chiều dài của mảnh đất là: 48 : 8 . 5 = 30 (m).
Chiều rộng của mảnh đất là: 48 – 30 = 18 (m).
Diện tích mảnh đất là: 30 . 18 = 540 (m2).
Diện tích phần đất xây nhà là: (m2).
Đáp số: 45m2.
Câu 25:
1 thửa ruộng hình chữ nhật có nửa chu vi là 250m. Chiều dài bằng chiều rộng. Trên thửa ruộng đó người ta cấy lúa cứ 100 mét vuông thu hoạch được 65 kg thóc. Hỏi thửa ruộng đó thu hoạch được tất cả bao nhiêu kg thóc?
 Xem đáp án
Xem đáp án
Chiều dài của thửa ruộng là:
250 : (3 + 2) . 3 = 150 (m)
Chiều rộng của thửa ruộng đó là:
250 – 150 = 100 (m)
Diện tích của thửa ruộng đó là:
150.100 = 15000 (m2)
Trên thửa ruộng đó thu hoạch được:
65 . (15000 : 100) = 9750 (kg)
Đáp số: 9750 kg thóc.
Câu 27:
Một người có 200 triệu đồng muốn đi gửi tiết kiệm.
a) Nếu người đó gửi tiền ở ngân hàng A thì được nhận lãi suất 7% một năm. Hỏi sau một năm thì người đó nhận về được bao nhiêu tiền? (cả số tiền gốc và số tiền lãi)
 Xem đáp án
Xem đáp án
a) Sau 1 năm thì người đó nhận được số tiền ở ngân hàng A là:
200.(100% + 7%) = 214 (triệu đồng)
Câu 28:
b) Nếu người đó gửi tiến ở ngân hàng B thì được nhận lãi suất 6% một năm và được nhận ngay 3 triệu đồng. Hỏi người đó nên gửi tiền ở ngân hàng nào để có số tiền nhận được sau một năm nhiều hơn?
 Xem đáp án
Xem đáp án
b) Sau 1 năm thì người đó nhận được số tiền ở ngân hàng B là:
200.(100% + 6%) + 3 = 215 (triệu đồng)
Ta có: 215 triệu > 214 triệu
Suy ra: Người đó nên gửi tiền ở ngân hàng B để có số tiền nhận về nhiều hơn sau một năm.
Câu 29:
Một người gửi 100 triệu đồng vào ngân hàng với lãi suất 0,4%/ tháng. Biết rằng nếu không rút tiền ta khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được lập vào vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau 6 tháng, người đó được lĩnh số tiền (cả vốn ban đầu và lãi) gần nhất với số tiền nào dưới đây, nếu trong khoảng thời gian này người đó không rút tiền ra và lãi xuất không thay đổi?
 Xem đáp án
Xem đáp án
Sau 6 tháng, người đó được lĩnh số tiền là:
100000000.(1 + 0,4%)6 ≈ 102424000 (đồng).
Câu 30:
Xay một tạ thóc thì được 73 kg gạo. Một người xay lần thứ nhất 25 tạ thóc, lần thứ hai xay 20,2 tạ thóc. Hỏi trong cả hai lần, người đó thu được bao nhiêu tạ gạo?
 Xem đáp án
Xem đáp án
Đổi: 73kg = 0,73 tạ
Cả 2 lần xay số tạ gạo là:
25 + 20,2 = 45,2 (tạ)
Cả 2 lần thu được số tạ gạo là:
45,2 . 0,73 = 32,99 (tạ).
Câu 31:
Một nhà máy lên kế hoạch dự định sản xuất hai loại sản phẩm A và B. Các sản phẩm này được chế tạo từ ba loại nguyên liệu I, II, III. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại cần dùng để sản xuất 1 kg sản phẩm được cho trong bảng sau :
|
Loại nguyên liệu |
Số kilôgam nguyên liệu dự trữ |
Số kilôgam nguyên liệu cần dùng sản xuất 1 kg sản phẩm |
|
|
A |
B |
||
|
I |
8 |
2 |
1 |
|
II |
24 |
4 |
4 |
|
III |
8 |
1 |
2 |
Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất ? Biết rằng, mỗi kilogam sản phẩm loại A lãi 30 triệu đồng, mỗi sản phẩm loại B lãi 50 triệu đồng.
 Xem đáp án
Xem đáp án
Gọi x (kg) là khối lượng sản phẩm A, y (kg) là khối lượng sản phẩm B mà công ty sản xuất.
Hiển nhiên x ≥ 0 và y ≥ 0.
Số nguyên liệu loại I cần dùng để sản xuất ra x kg sản phẩm A là 2x (kg).
Số nguyên liệu loại I cần dùng để sản xuất ra y kg sản phẩm B là y (kg).
Tổng nguyên liệu loại I cần dùng là 2x + y (kg).
Mặt khác, số nguyên liệu dự trữ loại I là 8 kg, nên ta có bất phương trình : 2x + y ≤ 8.
Tương tự,
Số nguyên liệu loại II cần dùng để sản xuất ra x kg sản phẩm A là 4x (kg).
Số nguyên liệu loại II cần dùng để sản xuất ra y kg sản phẩm B là 4y (kg).
Tổng nguyên liệu loại II cần dùng là 4x + 4y (kg).
Số nguyên liệu dự trữ loại II là 24 kg, nên ta có bất phương trình : 4x + 4y ≤ 24, tức là x + y ≤ 6.
Số nguyên liệu loại III cần dùng để sản xuất ra x kg sản phẩm A là x (kg).
Số nguyên liệu loại III cần dùng để sản xuất ra y kg sản phẩm B là 2y (kg).
Tổng nguyên liệu loại III cần dùng là x + 2y (kg).
Số nguyên liệu dự trữ loại III là 8 kg, nên ta có bất phương trình : x + 2y ≤ 8.
Vậy ta có hệ bất phương trình sau :
Biểu diễn miền nghiệm của hệ này trên mặt phẳng tọa độ Oxy ta được hình sau :
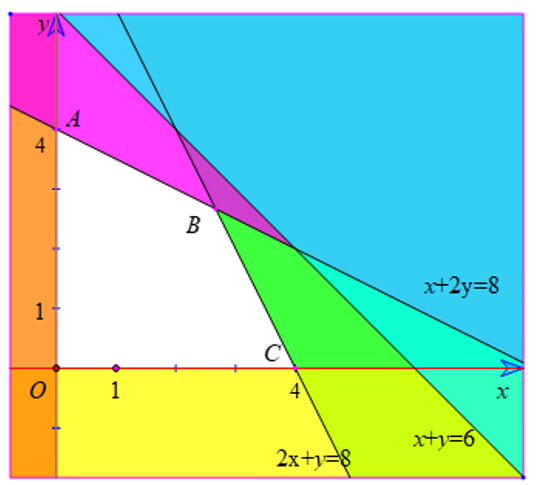
Miền nghiệm của hệ là miền tứ giác OABC (bao gồm các cạnh) với các đỉnh O(0 ; 0) ; A (0 ; 4); ; C(4 ; 0).
Gọi F là số tiền lãi thu được (đơn vị: triệu đồng), ta có:
Tiền lãi thu được từ x kg sản phẩm loại A là: 30x (triệu đồng)
Tiền lãi thu được từ y kg sản phẩm loại B là: 50y (triệu đồng).
Khi đó F = 30x + 50y
Tính giá trị của F tại các đỉnh của tứ giác OABC:
Tại O(0; 0) : F = 30.0 +50.0 = 0;
Tại A(0; 4) : F = 30 . 0 + 50 . 4 = 200;
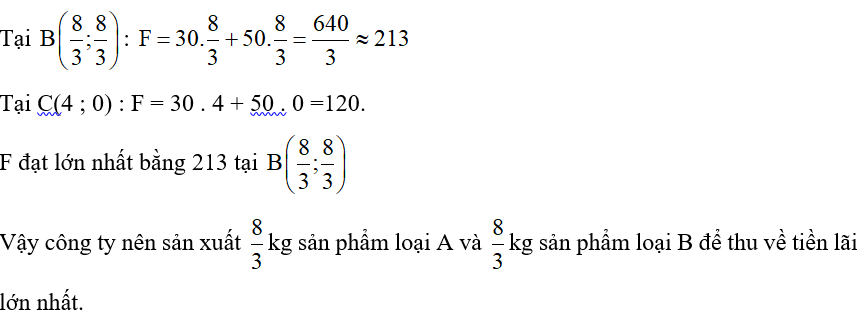
Câu 32:
 Xem đáp án
Xem đáp án
Công thức của phép tính cộng: a + b = Tổng
Trong đó a và b là số hạng. Giá trị của tổng sẽ bằng kết quả của phép tính a + b
Dạng bài một phép cộng có tổng bằng một số hạng nghĩa là Tổng = a hoặc bằng b.
Một số ví dụ của dạng bài toán này:
2 + 0 = 2
15 + 0 = 15
0 + 20 = 15
0 + 1 = 1
Câu 33:
Có bao nhiêu số tự nhiên có 4 chữ số mà tổng tất cả các chữ số của số đó bằng 7.
 Xem đáp án
Xem đáp án
Gọi số cần tìm có dạng
TH1: Trong 4 chữ số a, b, c, d có 3 chữ số bằng 0 ⇒ b = c = d = 0, a = 7
Do đó có 1 số thỏa mãn.
TH2: Trong 4 chữ số a, b, c, d có 2 chữ số bằng 0.
- Chọn vị trí cho 2 chữ số 0 có cách.
- Tổng hai chữ số còn lại là 7, ta có
7 = 6 + 1 = 5 + 2 = 4 + 3 = 3 + 4 = 2 + 5 = 1 + 6
nên có 6 cách chọn 2 chữ số còn lại.
Do đó trường hợp này có 18 số.
TH3: Trong 4 chữ số a, b, c, d có 1 chữ số bằng 0.
- Chọn vị trí cho 1 chữ số 0 có cách.
- Tổng 3 chữ số còn lại bằng 7, ta có:
7 = 1 + 1 + 5 = 1 + 2 + 4 = 1 + 3 + 3 = 2 + 2 + 3
+ Với bộ số (1;2;4) có 3! = 6 cách chọn 3 chữ số còn lại.
+ Với 3 bộ số còn lại có: cách chọn 3 chữ số còn lại.
Do đó trường hợp này có: 3.(6 + 3.3) = 45 số.
TH4: Trong 4 chữ số a, b, c, d không có chữ số nằm bằng 0.
Ta có: 7 = 1 + 1 + 1 + 4
7 = 1 + 1 + 2 + 3
7 = 1 + 2 + 2 + 2
+ Với bộ số (1; 1; 1; 4), có 4! 3! = 4 cách chọn 4 chữ số a, b, c, d.
+ Với bộ số (1; 1; 2; 3), có 4! 2! = 12 cách chọn 4 chữ số a, b, c, d.
+ Với bộ số (1; 2; 2; 2), có 4! 3! = 4 cách chọn 4 chữ số a, b, c, d.
Do đó trường hợp này có 4 + 12 + 4 = 20 số thỏa mãn.
Vậy có tất cả: 1 + 18 + 45 + 20 = 84 số.
Câu 34:
Một số học sinh của lớp 6A và 6B cùng tham gia trồng cây. Mỗi học sinh đều trồng được số cây như nhau. Biết rằng lớp 6A trồng được 45 cây, lớp 6B trồng được 48 cây. Hỏi mỗi lớp có bao nhiêu học sinh tham gia lao động trồng cây?
 Xem đáp án
Xem đáp án
Gọi số cây trồng được là a (cây, a ∈ ℕ*).
Vì lớp 6A trồng được 45 cây, lớp 6B trồng được 48 cây.
⇒ 45 ⋮ a; 48 ⋮ a
Ta có: 45 = 3² . 5
48 = 24 . 3
ƯCLN (45, 48 ) = 3
a ∈ Ư(3) = {1, 3}
+ Trường hợp mỗi bạn trồng 1 cây:
Lớp 6A có số học sinh tham gia lao động trồng cây là: 45 : 1 = 45 (học sinh).
Lớp 6B có số học sinh tham gia lao động trồng cây là: 48 : 1 = 48 (học sinh).
+ Trường hợp mỗi bạn trồng 3 cây:
Lớp 6A có số học sinh tham gia trồng cây là: 45 : 3 = 15 (học sinh).
Lớp 6B có số học sinh tham gia trồng cây là: 48 : 3 = 16 (học sinh).
Câu 35:
Số khi chia cho 6 dư 4 khi chia cho 7 dư 6 chia cho 11 dư 3. Tìm số dư trong phép chia số đó cho 462.
 Xem đáp án
Xem đáp án
Gọi số đó là a
* a chia cho 6 dư 4
⇒ a - 4 chia hết cho 6
⇒ a - 4 + 12 chia hết cho 6
⇒ a + 8 chia hết cho 6
* a chia cho 7 dư 6
⇒ a - 6 chia hết cho 7
⇒ a - 6 + 14 chia hết cho 7
⇒ a + 8 chia hết cho 7
* a chia cho 11 dư 3
⇒ a - 3 chia hết cho 11
⇒ a - 3 + 11 chia hết cho 11
⇒ a + 8 chia hết cho 11
Vậy a + 8 chia hết cho 6;7;11
⇒ a + 8 chia hết cho BCNN(6, 7, 11)
Ta có: 6 = 2.3; 7 = 7; 11 = 11
BCNN(6, 7, 11) = 2.3.7.11 = 462
⇒ a + 8 chia hết cho 462.
Tức là a chia 462 dư 8.
Câu 36:
Một thửa ruộng hình chữ nhật có chiều dài là 75m. Chiều rộng bằng chiều dài. Tính diện tích thửa ruộng?
 Xem đáp án
Xem đáp án
Chiều rộng thửa ruộng hình chữ nhật là:
Diện tích thửa ruộng là:
75.45 = 3375 (m2).
Câu 37:
Một thửa ruộng hình chữ nhật có chiều dài là 150m, chiều rộng bằng chiều dài người ta cấy lúa ở đó tính ra cứ 10 mét vuông thu hoạch được 5 kg thóc hỏi đã thu hoạch được ở thửa ruộng được bao nhiêu tạ thóc?
 Xem đáp án
Xem đáp án
Chiều rộng thửa ruộng là:
150 : 5 = 30 (m)
Diện tích thửa ruộng là:
30 . 150 = 4500 (m2)
Số kg thóc thu hoạch được là:
4500 : 10 . 5 = 2250 (kg) = 22,5 tạ.
Câu 39:
1 thửa ruộng hình chữ nhật có nửa chu vi là 150m, chiều rộng kém chiều dài 62m. Tính diện tích thửa ruộng hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chiều rộng thửa ruộng là:
(150 - 62 ) : 2 = 44 (m)
Chiều dài thửa ruộng là:
150 - 44 = 106 (m)
Diện tích thửa ruộng là:
44 . 106 = 4664 (m2)
Câu 40:
Một trường học có 476 học sinh nam. Số học sinh nam nhiều hơn số học sinh nữ là 43 học sinh. Hỏi trường đó có bao nhiêu học sinh nữ?
 Xem đáp án
Xem đáp án
Số học sinh nữ là: 476 − 43 = 433 học sinh.
Đáp số: 433 học sinh nữ.
Câu 41:
Mua 1kg đường hết 22000 đồng. Hỏi mua đường hết bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Mua đường hết số tiền là:
22000. (đồng).
Câu 42:
Mua 3 túi xà phòng và 2m vải thì hết 64 000 đồng. Nếu mua 2 túi xà phòng và 3m vải như vậy thì hết 71 000 đồng. Tính giá tiền 1 túi xà phòng và 1m vải?
 Xem đáp án
Xem đáp án
Tổng 5 túi xà phòng và 1m vải hết số tiền là:
64000 + 71000 = 135000 (đồng)
Tổng 1 túi xà phòng và 1m vải hết số tiền là:
135000 : 5 = 27000 (đồng)
Tiền mua 1m vải nhiều hơn tiền mua 1 túi xà phòng là:
71000 – 64000 = 7000 (đồng)
Giá tiền 1 túi xà phòng là:
(27000 − 7000) : 2 = 10000 (đồng)
Giá tiền 1m vải là:
27000 – 10000 = 17000 (đồng)
Vậy giá tiền 1 túi xà phòng: 10000 đồng; giá tiền 1m vải: 17000 đồng.
Câu 43:
 Xem đáp án
Xem đáp án
Với p = 2 ta có 2p + p2 = 12 không là số nguyên tố
Với p = 2 ta có 2p + p2 = 17 là số nguyên tố
Với p > 3 ta có p2 + 2p = (p2 – 1) + (2p + 1 )
Vì p lẽ và p không chia hết cho 3 nên p2 – 1 chia hết cho 3 và 2p + 1 chia hết cho 3. Do đó 2p + p2 là hợp số
Vậy với p = 3 thì 2p + p2 là số nguyên tố.
Câu 47:
Có bao nhiêu giá trị nguyên của tham số m để phương trình: có nghiệm thực?
 Xem đáp án
Xem đáp án
⇔
⇔ 3sin22x – 6sin2x – m – 4 = 0
⇔ 3sin22x – 6sin2x – 4 = m
Đặt t = sin2x (-1 ≤ m ≤ 1)
Khi đó: 3t2 – 6t – 4 = m
Xét sự biến thiên hàm số f(t) = 3t2 – 6t – 4
f’(t) = 6t – 6
f’(t) = 0 thì 6t – 6 = 0 ⇔ t = 1
Khi đó f (1) = −7 và f (−1) = 5
Vậy PT có nghiệm khi −7 ≤ m ≤ 5
Kết luận: Có 13 giá trị nguyên của m.
Câu 48:
So sánh 333444 và 444333
 Xem đáp án
Xem đáp án
333444 = 3334.111 = (3334)111
444333 = (4443)111
Ta so sánh 3334 và 4443
3334 = (3.111)4 = 34.1114 = 81.1114
4443 = 1113.43 = 64.1113
Mà 81.1114 > 64.1113 nên 3334 > 4443
⇒ (3334)111 > (4443)111
Vậy 333444 > 444333.
Câu 50:
Thực hiện phép tính rồi tìm giá trị nhỏ nhất của biểu thức
A = (9xy2 – 6x2y) : (-3xy) + (6x2y + 2x4) : (2x2).
 Xem đáp án
Xem đáp án
A = (9xy2 – 6x2y) : (-3xy) + (6x2y + 2x4) : (2x2)
A = 3xy(3y – 2x) : (-3xy) + (3y + x2)
A = 2x – 3y + 3y + x2
A = x2 + 2x
A = (x + 1)2 – 1
Vì (x + 1)2 ≥ 0 với mọi x nên (x + 1)2 – 1 ≥ -1 với mọi x
Vậy GTNN của A là -1 khi x = -1.
Câu 51:
Tìm GTLN của y = sin9x + cos12x.
 Xem đáp án
Xem đáp án
Do
Suy ra: y = sin9x + cos12x ≤ sin2x + cos2x = 1
Vậy ymax = 1 khi .
Câu 52:
 Xem đáp án
Xem đáp án
x5 + y2 = xy2 + 1
⇔ x5 – 1 = xy2 – y2
⇔ (x – 1)(x4 + x3 + x2 + x + 1) = y2(x – 1)
⇔ (x - 1)(x4 + x3 + x2 + x + 1 – y2) = 0
⇔
Với (1) ta thu được mọi y ∈ ℤ đều thỏa mãn
Vậy (x; y) = (1; y) (y ∈ ℤ)
Với (2):
Phương trình tương đương: 4y2 = 4x4 + 4x3 + 4x2 + 4x + 4
Dùng phương pháp kẹp ta có: (2x2 + x + 2)2 ≥ (2y)2 ≥ (2x2 + x)2
Do đó:
⇔
Vậy ta có cặp (x; y) = (0; 1), (0; -1).
Câu 53:
 Xem đáp án
Xem đáp án
+ Nếu y = 0 thì x2 – 5x + 7 = 1
⇔ x2 – 5x + 6 = 0
⇔
+ Nếu y = 1 thì x2 – 5x + 7 = 3
⇔ x2 – 5x + 4 = 0
⇔
+ Nếu y > 1 thì 3y = (x – 2)(x – 3) + 1
Suy ra: x ≡ 1 (mod 3)
Hay x = 3k + 1 (k ∈ ℕ)
Thay vào ta có: 9k2 – 9k + 3 = 3y
⇔ 3k2 – 3k + 1 = 3y-1
Nhận thấy 3y-1 chia hết cho 3 mà 3k2 – 3k + 1 ≡ 1 (mod 3)
Nên vô lý
Vậy (x;y) ∈ {(2;0), (3;0), (1;1), (4;1)}.
Câu 54:
Tìm chữ số tận cùng của 172002.
 Xem đáp án
Xem đáp án
172002 = 172000.172 = (174)500.289 = (…..1). 289 = (…..9)
Vậy chữ số tận cùng của 172002 là 9.
Câu 56:
Tìm GTLN của A = 5 – 2x2 – 4y2 + 4xy – 8x – 12y.
 Xem đáp án
Xem đáp án
A = 5 – 2x2 – 4y2 + 4xy – 8x – 12y
A = 5 – [(x2 – 4xy + 4y2) + (-6x + 12y) + (x2 + 14x + 49) – 49]
A = 5 – [(x – 2y)2 – 6(x – 2y) + (x + 7)2 – 49]
A = 5 – [(x – 2y + 3)2 + (x + 7)2] + 58
A = 63 - [(x – 2y + 3)2 + (x + 7)2]
Vì (x – 2y + 3)2 + (x + 7)2 ≥ 0 với mọi x, y nên 63 - [(x – 2y + 3)2 + (x + 7)2] ≤ 63 với mọi x, y.
Hay A ≤ 63
Vậy GTLN của A là 63 khi .
Câu 58:
Tìm m để đồ thị hàm số y = x3 – 2mx2 + (m + 2)x cắt trục hoành tại 3 điểm phân biệt.
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm:
x3 – 2mx2 + (m + 2)x = 0
⇔ x(x2 – 2mx + m + 2) = 0
⇔
Phương trình có 3 nghiệm phân biệt khi (*) có 2 nghiệm phân biệt khác 0
Suy ra: .
Câu 59:
Tìm m để đường thẳng y = m(x + 1) – 2 cắt đồ thị hàm số y = x3 + 3x2 – 4 tại ba điểm phân biệt.
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm:
m(x + 1) – 2 = x3 + 3x2 – 4
⇔ x3 + 3x2 – mx – m – 2 = 0
⇔ (x + 1)(x2 + 2x - m – 2) = 0
⇔
Phương trình có 3 nghiệm phân biệt khi x2 + 2x – m – 2 = 0 có 2 nghiệm phân biệt khác -1.
Suy ra:
Vậy m > -3.
Câu 60:
Tìm m để phương trình x3 + 2x2 + (m + 1)x + 2(m + 1) = 0 có ba nghiệm lập thành cấp số nhân.
 Xem đáp án
Xem đáp án
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số nhân, khi đó:
Từ x1 + x2 + x3 = -2 nên x1 + x3 = -2 – x2
Ta có: x1x2 + x2x3 + x3x1 = m + 1
⇔ x2(-2 – x2) + x22 = m + 1
⇔ -2x2 = m + 1
⇔
Thay vào phương trình ta có:
Giải phương trình trên ta được: m = -1; m = 3; m = -4.
+ Ngược lại: Với m = -1 thay vào phương trình đã cho ta được:
x3 + 2x2 = 0 ⇔
Ba nghiệm này lập thành cấp số nhân với công bội q = 0 (thỏa mãn)
+ Với m = 3 thay vào phương trình đã cho ta được: x3 + 2x2 + 4x + 8 = 0
⇔ x = -2 (loại)
+ Với m = - 4 thay vào phương trình đã cho ta được: x3 + 2x2 – 3x - 6 = 0
⇔ (không thỏa mãn)
Vậy m = -1.
Câu 61:
Tìm n để 2n + 9 là số chính phương.
 Xem đáp án
Xem đáp án
Nếu n = 2k + 1
⇒ 9 +22k+1 = 2.4k + 9 chia 3 dư 2 nên không thể là số chính phương
⇒ n = 2k
Đặt 9 + 22k = x2
⇒ (x − 2k)(x + 2k) = 1.9 = 3.3
Do 0 < x − 2k < x + 2k nên ta có:
Vậy n = 4.
Câu 62:
Tìm số nguyên dương x để 3x + 171 là một số chính phương.
 Xem đáp án
Xem đáp án
Đặt 3x + 171 = y2
Do 171 chia hết cho 3; 3x chia hết cho 3 ⇒ y chia hết cho 3
⇒ y2 chia hết cho 9
Mà 171 cũng chia hết cho 9
⇒ 3x cũng phải chia hết cho 9
⇒ x là số chẵn.
Đặt x = 2a; y = 3b với a, b nguyên dương
32a + 171 = (3b)2
⇔ 32a-2 + 19 = b2
⇔ b2 - 32a-2 = 19
⇔ (b – 3a-1)(b + 3a-1) = 19*
Do b + 3a-1 > b - 3a-1 với mọi a, b nguyên dương nên b - 3a-1 = 1; b + 3a-1 = 19
Suy ra: b = 10; 3a-1 = 9
Khi đó: x = 6; y = 30.
Vậy (x; y) = (6; 30).
Câu 63:
Tìm số tự nhiên n sao cho A = n2 + 10n là số nguyên tố.
 Xem đáp án
Xem đáp án
n2 + 10n = n.n + 10n = n.(n + 10)
Để n(n + 10) là số nguyên tố ⇒ n + 10 là số nguyên số
Mà nếu n + 10 là số nguyên tố thì n(n+10) không nguyên tố
Suy ra: n = 1
Vậy giá trị duy nhất của n là n = 1.
Câu 64:
Tìm tất cả các giá trị của tham số m để hàm số y = -x3 – 3x2 + m đồng biến trên [-1; 1] bằng 0.
 Xem đáp án
Xem đáp án
Ta có: y’ = -3x2 – 6x
Xét y’ = 0
⇔ -3x2 – 6x = 0
⇔
f(-1) = m – 2; f(0) = m; f(1) = m – 4
Ta thấy: m – 4 = min{f(-1); f(0); f(1)}
Suy ra: m – 4 = 0 hay m = 4
Vậy m = 4.
Câu 65:
Tìm tất cả các giá trị của tham số m để hàm số y = mx2 - (m2 + 1)x + 3 đồng biến trên (1; +∞).
 Xem đáp án
Xem đáp án
y = mx2 - (m2 + 1)x + 3
Do a = m > 0 (1)
Hàm số đồng biến trên miền
Để hàm số đồng biến trên (1; +∞) điều kiện là (1; +∞) ⊂
Suy ra:
⇔ m2 + 1 ≤ 2m
⇔ m2 – 2m + 1 ≤ 0
⇔ (m – 1)2 ≤ 0
⇔ m – 1 ≤ 0
⇔ m ≤ 1 (2)
Từ (1) và (2) ta có: 0 < m ≤ 1
Vậy 0 < m ≤ 1.
Câu 66:
Hàm số y = ln(x2 – 2x + m) có tập xác định là ℝ khi
A. m > 1.
B. m ≥ 1.
C. m > 0.
D. m ≥ 0.
 Xem đáp án
Xem đáp án
Đáp án A.
Hàm số xác định trên ℝ
Suy ra: x2 – 2x + m > 0, ∀x ∈ ℝ
⇔ .
Câu 67:
Tìm x biết: x3 – 4x = 0.
 Xem đáp án
Xem đáp án
x3 – 4x = 0
⇔ x(x2 – 4) = 0
⇔ x(x – 2)(x + 2) = 0
⇔
Vậy x ∈ {0; 2; -2}.
Câu 69:
Tìm x biết (x + 2)(x - 1) < 0.
 Xem đáp án
Xem đáp án
Tích của hai số nhỏ hơn 0 khi và chỉ khi hai số đó trái dấu
Mà x + 2 > x – 1
Nên x – 1 < 0 và x + 2 > 0
Suy ra: -2 < x < 1.
Vậy -2 < x < 1.
Câu 70:
 Xem đáp án
Xem đáp án
A = 3 + 32 + 33 + … + 399
3A = 32 + 33 + 34 … + 3100
3A – A = (32 + 33 + 34 … + 3100) – (3 + 32 + 33 + … + 399)
2A = 3100 – 3
.
Câu 71:
Cho là tổng của n số chính phương đầu tiên. Khi đó tổng của 10 số chính phương đầu tiên là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng của 10 số chính phương đầu tiên là: .
Câu 72:
Xét tính tuần hoàn và chu kỳ của y = cos2x – 1.
 Xem đáp án
Xem đáp án
Tập xác định: D = ℝ
Ta có: y = cos2x – 1
Với mọi x ∈ ℝ thì x + π ∈ ℝ
Suy ra hàm số tuần hoàn với chu kì T = π
Vậy hàm số tuần hoàn với chu kì T = π.
Câu 76:
 Xem đáp án
Xem đáp án
x6 – 1
= (x3)2 – 12
= (x3 – 1)(x3 + 1)
= (x – 1)(x2 + x + 1)(x + 1)(x2 – x + 1).
Câu 77:
Cho phương trình: x2 + (2m – 8)x + 8m3 = 0. Tìm m để phương trình có nghiệm thỏa mãn x1 = x22.
 Xem đáp án
Xem đáp án
x2 + (2m – 8)x + 8m3 = 0 (*)
Để (*) có nghiệm thì ∆' ≥ 0 ⇔ (m – 4)2 + 8m3 ≥ 0
Với x1 và x2 là các nghiệm của (*), theo định lý Vi-ét và kết hợp với đề bài, có:
Thay (3) vào (2) ta có: x23 = -8m3
Suy ra: x2 = -2m
⇒ x1 = 4m2
Thay vào (1) ta có: 4m2 – 2m = 8 – 2m
⇔ 4m2 = 8
⇔ m2 = 2
⇔
Vậy .
Câu 79:
Tìm x ∈ ℤ biết x2 + 3 chia hết cho x + 1.
 Xem đáp án
Xem đáp án
Ta có: x2 + 3 = x2 – 1 + 4 = (x – 1)(x + 1) + 4
Vì (x – 1)(x + 1) chia hết cho x + 1
Nên 4 ⋮ (x + 1) hay x + 1 ∈ Ư(4) = {1; 4; -1; -4; 2; -2}.
Vậy x ∈ {0; 3; -2; -5; 1; -3}.
Câu 80:
 Xem đáp án
Xem đáp án
x2 + 4x – 12 = 0
⇔ (x2 + 4x + 4) – 16 = 0
⇔ (x + 2)2 – 42 = 0
⇔ (x + 2 + 4)(x + 2 – 4) = 0
⇔ (x + 6)(x – 2) = 0
⇔
Vậy x = 2 hoặc x = -6.
Câu 81:
Giải phương trình: x2 + 5x + 6 = 0.
 Xem đáp án
Xem đáp án
x2 + 5x + 6 = 0
⇔ x2 + 2x + 3x + 6 = 0
⇔ x(x + 2) + 3(x + 2) = 0
⇔ (x + 2)(x + 3) = 0
⇔
Vậy x = -2 hoặc x = -3.
Câu 82:
Với mọi số x,y. Chứng minh rằng x2 + 5y2 – 4xy + 2x – 6y + 3 > 0.
 Xem đáp án
Xem đáp án
x2 + 5y2 – 4xy + 2x – 6y + 3
= (x2 + 4y2 + 1 – 4xy + 2x – 4y) + (y2 – 2y + 1) + 1
= (x – 2y + 1)2 + (y – 1)2 + 1
Ta thấy (x – 2y + 1)2 + (y – 1)2 ≥ 0 với mọi x, y
Suy ra: x – 2y + 1)2 + (y – 1)2 + 1 ≥ 1 > 0 với mọi x, y
Vậy x2 + 5y2 – 4xy + 2x – 6y + 3 > 0 với mọi x, y.
Câu 83:
Tìm các số tự nhiên x, y thỏa mãn: x2 + x – 89 = 5y.
 Xem đáp án
Xem đáp án
Vì x và y nguyên không âm nên x ≥ 9
+) Với x = 9 thì ta tìm được y = 0
+) Xét x > 9. Khi đó x chia cho 5 có 5 loại số dư là 0, 1, 2, 3, 4
TH1: x chia hết cho 5 hay x có dạng 5k với k là số tự nhiên.
Ta có: x2 + x - 89 = 25k2 + 5k - 89
Dễ thấy 25k2 + 5k chia hết cho 5 còn 89 không chia hết cho 5 nên vế trái không chia hết cho 5 ⇒ không có cặp (x, y) thỏa mãn
TH2: x chia 5 dư 1 hay x = 5k + 1 (k ∈ ℕ)
Ta có: x2 + x - 89 = 25k2 + 10k + 1 + 5k + 1 – 89 = 25k2 + 15k – 87
Dễ thấy 25k2 + 15k chia hết cho 5 còn 87 không chia hết cho 5 nên vế trái không chia hết cho 5 ⇒ không có cặp (x, y) thỏa mãn
TH3: x chia 5 dư 2 hay x = 5k + 2 (k ∈ ℕ)
Ta có: x2 + x - 89 = 25k2 + 20k + 4 + 5k + 2 – 89 = 25k2 + 25k – 83
Dễ thấy 25k2 + 25k chia hết cho 5 còn 83 không chia hết cho 5 nên vế trái không chia hết cho 5 ⇒ không có cặp (x, y) thỏa mãn
TH4: x chia 5 dư 3 hay x = 5k + 3 (k ∈ ℕ)
Ta có: x2 + x - 89 = 25k2 + 30k + 9 + 5k + 3 – 89 = 25k2 + 35k – 77
Dễ thấy 25k2 + 15k chia hết cho 5 còn 87 không chia hết cho 5 nên vế trái không chia hết cho 5 ⇒ không có cặp (x, y) thỏa mãn
TH2: x chia 5 dư 4 hay x = 5k + 4 (k ∈ ℕ)
Ta có: x2 + x - 89 = 25k2 + 40k + 16 + 5k + 14 – 89 = 25k2 + 45k – 59
Dễ thấy 25k2 + 45k chia hết cho 5 còn 59 không chia hết cho 5 nên vế trái không chia hết cho 5 ⇒ không có cặp (x, y) thỏa mãn
Vậy (x;y) = (9;0).
Câu 84:
Cho x2 + y2 + z2 = xy + yz + zx. Chứng minh x = y = z.
 Xem đáp án
Xem đáp án
x2 + y2 + z2 = xy + yz + zx
⇔ 2x2 + 2y2 + 2z2 = 2xy + 2yz + 2zx
⇔ (x2 – 2xy + y2) + (y2 – 2yz + z2) + (z2 – 2xz + x2) = 0
⇔ (x – y)2 + (y – z)2 + (z – x)2 = 0 (*)
Vì (x – y)2 + (y – z)2 + (z – x)2 ≥ 0 với mọi x, y, z nên để (*) xảy ra thì (x – y)2 = (y – z)2 = (z – x)2 = 0
Tức là: .
Câu 85:
Tìm GTNN của A = x2 + y2 + z2 – yz – 4x – 3y + 2030.
 Xem đáp án
Xem đáp án
A = x2 + y2 + z2 – yz – 4x – 3y + 2030
2A = 2x2 + 2y2 + 2z2 – 2yz – 8x – 6y + 4060
2A = 2(x – 2)2 + (y – 3)2 + (y – z)2 + z2 + 4043
Vì 2(x – 2)2 + (y – 3)2 + (y – z)2 + z2 ≥ 0 với mọi x, y, z
Nên 2(x – 2)2 + (y – 3)2 + (y – z)2 + z2 + 4043 ≥ 4043
Suy ra:
Vậy GTNN của A là
Dấu ‘=” xảy ra khi .
Câu 87:
Cho phương trình x2 – (3m + 1)x + 2m2 + m – 1 = 0 (1).
a) Chứng minh (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Gọi x1, x2 là các nghiệm của (1). Tìm m để biểu thức B = x12 + x22 – 3x1x2 đạt GTLN.
 Xem đáp án
Xem đáp án
a) Phương trình có 2 nghiệm phân biệt ∀ m khi :
Δ > 0 ⇔ [- (3m + 1)]² - 4 (2m² + m - 1) > 0
⇔ Δ = 9m² + 6m + 1 - 8m² - 4m + 4
= m² + 2m + 5
= (m + 1)2 + 4 ≥ 4 > 0 ∀m
Vậy (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m
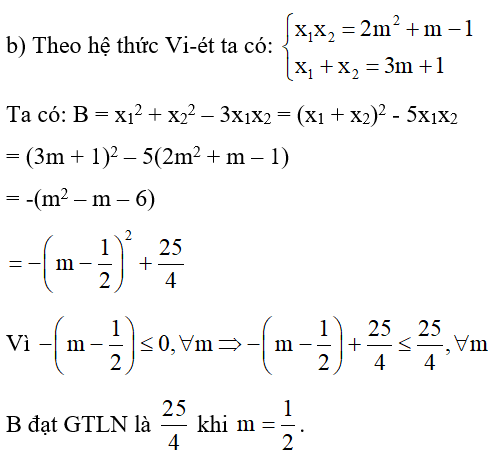
Câu 88:
Tìm x biết: x2(2x – 3) – 12 + 8x = 0
 Xem đáp án
Xem đáp án
x2(2x – 3) – 12 + 8x = 0
⇔ x2(2x – 3) + 4(2x – 3) = 0
⇔ (2x – 3)(x2 + 4) = 0
⇔ 2x – 3 = 0 (vì x2 + 4 > 4)
⇔
Vậy .
Câu 89:
Giải phương trình: x20 – 32x15 = 0.
 Xem đáp án
Xem đáp án
x20 – 32x15 = 0
⇔ x20 – 25.x15 = 0
⇔x15(x5 – 25) = 0
⇔
⇔
Vậy x = 0 hoặc x = 2.
Câu 90:
Phân tích đa thức thành nhân tử: 36 – x2 – 25y2 + 10xy.
 Xem đáp án
Xem đáp án
36 – x2 – 25y2 + 10xy
= 36 – (x2 + 25y2 – 10xy)
= 62 – (x – 5y)2
= (6 – x + 5y)(6 + x – 5y).
Câu 91:
Phân tích đa thức thành nhân tử: x2 – y2 – 4x + 4.
 Xem đáp án
Xem đáp án
x2 – y2 – 4x + 4
= (x2 – 4x + 4) – y2
= (x – 2)2 – y2
= (x – 2 + y)(x – 2 – y).