- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 3)
-
12964 lượt thi
-
76 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Từ điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn (O) (A và B là hai tiếp điểm).
a) Chứng minh tứ giác MAOB nội tiếp.
 Xem đáp án
Xem đáp án
a)
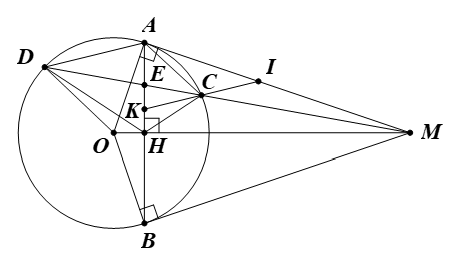
Ta có (MA là tiếp tuyến của (O)).
Suy ra ba điểm M, A, O cùng thuộc đường tròn đường kính OM (1)
Ta có (MB là tiếp tuyến của (O)).
Suy ra ba điểm M, B, O cùng thuộc đường tròn đường kính OM (2)
Từ (1), (2), suy ra tứ giác MAOB nội tiếp đường tròn đường kính OM.
Câu 2:
b) Từ M kẻ cát tuyến MCD với đường tròn (C nằm giữa M và D), tia MD nằm giữa hai tia MA và MO. Tia MO cắt AB tại H. Chứng minh MC.MD = MH.MO.
 Xem đáp án
Xem đáp án
b) Xét ∆MAC và ∆MDA, có:
chung;
(góc tạo bởi tia tiếp tuyến AM và dây cung AC và góc nội tiếp chắn cung AC).
Do đó (g.g).
Suy ra .
Vì vậy MA2 = MC.MD (3)
Ta có OA = OB = R.
Suy ra O nằm trên đường trung trực của đoạn AB (*)
Lại có MA = MB (tính chất hai tiếp tuyến cắt nhau).
Suy ra M nằm trên đường trung trực của đoạn AB (**)
Từ (*), (**), suy ra OM là đường trung trực của đoạn AB.
Mà OM cắt AB tại H.
Do đó OM ⊥ AB tại H.
∆OAM vuông tại A có AH là đường cao: MA2 = MH.MO (4)
Từ (3), (4), suy ra MC.MD = MH.MO.
Câu 3:
c) Qua C kẻ đường thẳng song song với AD cắt AM tại I, cắt AB tại K. Chứng minh C là trung điểm của IK.
 Xem đáp án
Xem đáp án
c) Gọi E là giao điểm của MD và AB.
Xét ∆MCH và ∆MOD, có:
chung;
(MC.MD = MH.MO).
Do đó (g.g).
Suy ra (cặp góc tương ứng) (5)
Vì vậy tứ giác DCHO nội tiếp đường tròn.
Do đó (cùng chắn ) (6)
Ta có OC = OD = R.
Suy ra ∆OCD cân tại O.
Do đó (7)
Từ (5), (6), (7), suy ra .
Mà và .
Suy ra
Do đó HA là đường phân giác trong của ∆CDH.
Lại có AH ⊥ HM tại H.
Suy ra HM là đường phân giác ngoài của ∆CDH.
Áp dụng tính chất đường phân giác, ta được (8)
Ta lại có IK // AD (giả thiết).
Áp dụng định lí Thales, ta được và (9)
Từ (8), (9), suy ra
Do đó CI = CK.
Vậy C là trung điểm của IK.
Câu 4:
Từ điểm M nằm ngoài đường tròn (O), kẻ hai tiếp tuyến MA, MB với đường tròn (O) (A và B là hai tiếp điểm).
a) Chứng minh tứ giác MAOB nội tiếp.
 Xem đáp án
Xem đáp án
a)
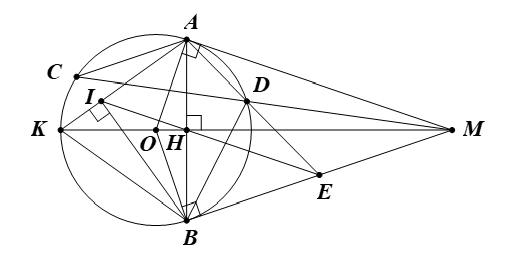
Ta có (MA là tiếp tuyến của (O)).
Suy ra ba điểm M, A, O cùng thuộc đường tròn đường kính OM (1)
Ta có (MB là tiếp tuyến của (O)).
Suy ra ba điểm M, B, O cùng thuộc đường tròn đường kính OM (2)
Từ (1), (2), suy ra tứ giác MAOB nội tiếp đường tròn đường kính OM.
Câu 5:
b) Kẻ dây AC song song với BM. Đường thẳng MC cắt đường tròn (O) tại điểm thứ hai là D (D ≠ C). Gọi E là giao điểm của AD và MB. Chứng minh BE2 = DE.AE và BE = ME.
 Xem đáp án
Xem đáp án
b) Xét ∆EBD và ∆EAB, có:
chung;
(góc tạo bởi tia tiếp tuyến BE và dây cung BD và góc nội tiếp chắn cung BD).
Do đó (g.g).
Suy ra .
Vì vậy BE2 = AE.DE.
Ta có (góc tạo bởi tia tiếp tuyến AM và dây cung AD và góc nội tiếp chắn cung AD).
Mà (ME // AC và cặp góc này là cặp góc so le trong).
Suy ra .
Xét ∆EMD và ∆EAM, có:
chung;
(chứng minh trên).
Do đó (g.g).
Suy ra .
Vì vậy ME2 = AE.DE.
Mà BE2 = AE.DE (chứng minh trên).
Suy ra ME2 = BE2.
Vì vậy ME = BE.
Vậy ta có điều phải chứng minh.
Câu 6:
c) Gọi H và K lần lượt là giao điểm của MO với AB và đường tròn (O) (H nằm giữa M và K), HE cắt AK tại I. Chứng minh AK vuông góc với BI.
 Xem đáp án
Xem đáp án
c) Ta có OA = OB = R.
Suy ra O nằm trên đường trung trực của đoạn AB (*)
Lại có MA = MB (tính chất hai tiếp tuyến cắt nhau).
Suy ra M nằm trên đường trung trực của đoạn AB (**)
Từ (*), (**), suy ra OM là đường trung trực của đoạn AB.
Mà OM cắt AB tại H.
Do đó OM ⊥ AB tại H và H là trung điểm của đoạn AB.
Mà E là trung điểm của đoạn MB (do ME = BE).
Suy ra HE là đường trung bình của ∆ABM.
Do đó HE // AM.
Vì vậy (cặp góc đồng vị).
Mà (góc tạo bởi tia tiếp tuyến AM và dây cung AB và góc nội tiếp chắn cung AB).
Suy ra .
Do đó tứ giác BHIK nội tiếp đường tròn.
Vì vậy (cùng chắn ).
Vậy AK ⊥ BI.
Câu 7:
Cho hai điểm A(–1; –2) và B(–4; 3). Lập phương trình đường thẳng (d) đi qua A, B.
 Xem đáp án
Xem đáp án
Với A(–1; –2) và B(–4; 3) ta có
Đường thẳng (d) đi qua A, B nên nhận làm vectơ chỉ phương, do đó nhận làm vectơ pháp tuyến
Khi đó phương trình đường thẳng (d) là:
5(x + 1) + 3(y + 2) = 0 Û 5x + 3y + 11 = 0.
Câu 8:
Phương trình 4sin22x – 3sin2x.cos2x – cos22x = 0 có bao nhiêu nghiệm trong khoảng (0; π)?
 Xem đáp án
Xem đáp án
Ta có 4sin22x – 3sin2x.cos2x – cos22x = 0 (1)
Trường hợp 1: cos2x = 0.
Phương trình (1) tương đương với: 4sin22x = 0.
⇔ sin2x = 0 (loại vì cos2x = 0).
Trường hợp 2: cos2x ≠ 0.
Chia hai vế của phương trình (1) cho cos22x, ta được: 4tan22x – 3tan2x – 1 = 0.
.
So với điều kiện cos2x ≠ 0, ta nhận .
• Vì x ∈ (0; π) nên
.
Mà k ∈ ℤ, suy ra k ∈ {0; 1}.
Do đó .
• Vì x ∈ (0; π) nên .
.
.
Mà k ∈ ℤ.
Suy ra k ∈ {1; 2}.
Do đó .
Vậy trong (0; π), phương trình đã cho có nghiệm là: .
Do đó ta chọn phương án D.
Câu 9:
Cho đường tròn (O) và dây AB không đi qua tâm, gọi M là trung điểm AB. Qua M vẽ dây CD không trùng AB. Chứng minh rằng M không là trung điểm của CD.
 Xem đáp án
Xem đáp án
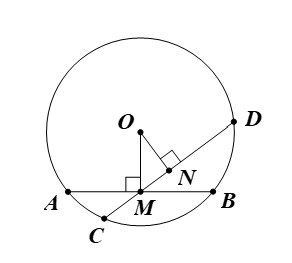
Giả sử M là trung điểm của CD.
Suy ra OM ⊥ CD.
Mà OM ⊥ AB (do M là trung điểm AB).
Khi đó CD trùng với AB (mâu thuẫn với giả thiết).
Vậy M không là trung điểm của CD.
Câu 10:
Khai triển biểu thức lượng giác cos4x theo cosx.
 Xem đáp án
Xem đáp án
Ta có cos4x = 2cos22x – 1
= 2(2cos2x – 1)2 – 1
= 2(4cos4x – 4cos2x + 1) – 1
= 8cos4x – 8cos2x + 2 – 1
= 8cos4x – 8cos2x + 1.
Vậy cos4x = 8cos4x – 8cos2x + 1.
Câu 11:
Cho G là trọng tâm của tam giác ABC. Chứng minh rằng diện tích tam giác GAC bằng diện tích tam giác ABC.
 Xem đáp án
Xem đáp án
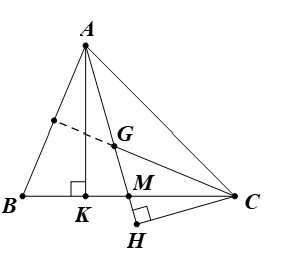
Gọi M là trung điểm BC. Suy ra .
Kẻ CH ⊥ AM.
Tam giác ABC có G là trọng tâm.
Suy ra .
Ta có .
Kẻ AK ⊥ BC.
Ta có .
Vì vậy .
Vậy diện tích tam giác GAC bằng diện tích tam giác ABC.
Câu 12:
Viết số thích hợp vào chỗ chấm:
a) 178 dm = … m … dm;
6789 cm = … m … dm … cm;
375 dam = … km … dam;
1987 m = … km … hm … m.
 Xem đáp án
Xem đáp án
a) 178 dm = 17 m 8 dm;
6789 cm = 67 m 8 dm 9 cm;
375 dam = 3 km 75 dam;
1987 m = 1 km 9 hm 87 m.
Câu 13:
Viết số thích hợp vào chỗ chấm:
b) 245 dag = … kg … g;
318 g = … hg … dag … g;
408 kg = … tạ … kg;
8194 kg = … tấn … tạ … kg.
 Xem đáp án
Xem đáp án
b) 245 dag = 2 kg 450 g;
318 g = 3 hg 1 dag 8 g;
408 kg = 4 tạ 8 kg;
8194 kg = 8 tấn 1 tạ 94 kg.
Câu 14:
Cho hình lập phương ABCD.A’B’C’D’ có diện tích tam giác ACD’ bằng . Tính thể tích V của hình lập phương.
 Xem đáp án
Xem đáp án
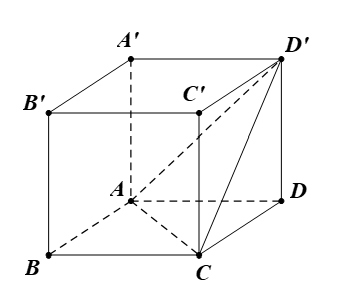
Gọi x là độ dài cạnh của hình lập phương ABCD.A’B’C’D’ (x > 0).
Ta có .
Suy ra ∆ACD’ đều.
Do đó .
Theo đề, ta có .
.
.
⇔ x2 = 2a2.
.
Vậy thể tích của hình lập phương ABCD.A’B’C’D’ là: .
Do đó ta chọn phương án C.
Câu 15:
Cho hình thang vuông ABCD, . Gọi M, N lần lượt là trung điểm của các cạnh BC, AD. Chứng minh:
a) Tam giác MAD là tam giác cân.
 Xem đáp án
Xem đáp án
a)
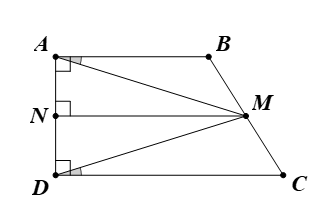
Ta có M, N lần lượt là trung điểm của BC và AD.
Suy ra MN // AB // CD.
Mà BA ⊥ AD (do ).
Do đó MN ⊥ AD.
Mà N là trung điểm của AD (giả thiết).
Vì vậy MN là đường trung trực của đoạn AD.
Suy ra MA = MD.
Vậy ∆MAD cân tại M.
Câu 16:
Chứng minh:
b) .
 Xem đáp án
Xem đáp án
b) Ta có (1)
Lại có (2)
Ta có ∆MAD cân tại M (kết quả câu a).
Suy ra (3)
Từ (1), (2), (3), suy ra .
Câu 17:
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
a) .
 Xem đáp án
Xem đáp án
a)
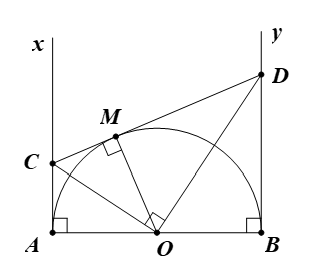
Ta có OA ⊥ Ax, OB ⊥ By (giả thiết).
Suy ra Ax, By là các tiếp tuyến của nửa đường tròn (O) lần lượt tại A và B.
Ta có AC, MC là hai tiếp tuyến của (O) và hai tiếp tuyến này cắt nhau tại C.
Suy ra CM = CA và (theo tính chất hai tiếp tuyến cắt nhau).
Chứng minh tương tự, ta được DM = DB và .
Ta có .
.
.
.
Vậy ta có điều phải chứng minh.
Câu 18:
Chứng minh rằng:
b) CD = AC + BD.
 Xem đáp án
Xem đáp án
b) Ta có CD = CM + MD = AC + BD.
Vậy CD = AC + BD.
Câu 19:
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
 Xem đáp án
Xem đáp án
c) Ta có CD là tiếp tuyến của (O) tại M, suy ra OM ⊥ CD.
∆COD vuông tại O có OM là đường cao nên:
OM2 = CM.CD (hệ thức lượng trong tam giác vuông).
⇔ R2 = AC.BD.
Ta thấy R không đổi khi điểm M di chuyển trên nửa đường tròn (O).
Vậy tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn (O).
Câu 20:
Cho nửa đường tròn tâm O đường kính AB, C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I, K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I). Tia AK cắt nửa đường tròn tâm O tại M, tia BM cắt tia CI tại D. Chứng minh:
a) Các tứ giác ACMD, BCKM nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
a)
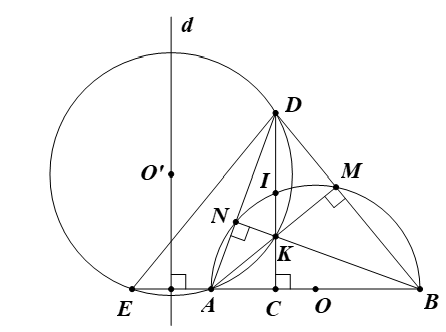
Ta có (CD ⊥ AB tại C).
Suy ra ba điểm A, C, D cùng thuộc đường tròn đường kính AD (1)
Ta có (góc nội tiếp chắn nửa đường tròn (O)).
Hay .
Suy ra ba điểm A, M, D cùng thuộc đường tròn đường kính AD (2)
Từ (1), (2), ta suy ra tứ giác ACMD nội tiếp đường tròn đường kính AD.
Ta có (CD ⊥ AB tại C).
Suy ra ba điểm B, C, K cùng thuộc đường tròn đường kính BK (3)
Ta có (góc nội tiếp chắn nửa đường tròn (O)).
Suy ra ba điểm K, M, B cùng thuộc đường tròn đường kính BK (4)
Từ (3), (4), ta suy ra tứ giác BCKM nội tiếp đường tròn đường kính BK.
Câu 21:
Chứng minh:
b) CK.CD = CA.CB.
 Xem đáp án
Xem đáp án
b) Xét ∆CKA và ∆CBD, có:
.
(do và (đối đỉnh));
Do đó (g.g).
Suy ra .
Vậy CK.CD = CA.CB.
Câu 22:
c) Gọi N là giao điểm của AD và đường tròn tâm O. Chứng minh B, K, N thẳng hàng.
 Xem đáp án
Xem đáp án
c) ∆ABD có hai đường cao AM, DC cắt nhau tại K.
Suy ra K là trực tâm của ∆ABD.
Do đó BK ⊥ AD (5)
Ta có (góc nội tiếp chắn nửa đường tròn (O)).
Suy ra AD ⊥ BN (6)
Từ (5), (6), suy ra ba điểm B, K, N thẳng hàng.
Câu 23:
d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI.
 Xem đáp án
Xem đáp án
d) Trên tia đối của tia CB, lấy điểm E sao cho CE = CB.
Ta có CK.CD = CA.CB (kết quả câu b).
Suy ra CK.CD = CA.CE.
Xét ∆CAK và ∆CDE, có:
chung;
(do CK.CD = CA.CE).
Do đó (c.g.c).
Suy ra (cặp góc tương ứng).
Vì vậy tứ giác AKDE nội tiếp đường tròn.
Vậy tâm đường tròn O’ ngoại tiếp tam giác AKD nằm trên đường trung trực d của đoạn AE cố định.
Câu 24:
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HM vuông góc với AB, HN vuông góc với AC. Chứng minh rằng tam giác AMN đồng dạng với tam giác ABC.
 Xem đáp án
Xem đáp án

∆ABH vuông tại H có HM là đường cao: AH2 = AM.AB (hệ thức lượng trong tam giác vuông) (1)
∆ACH vuông tại H có HN là đường cao: AH2 = AN.AC (hệ thức lượng trong tam giác vuông) (2)
Từ (1), (2), suy ra AM.AB = AN.AC.
Xét ∆AMN và ∆ABC, có:
;
(do AM.AB = AN.AC).
Vậy (c.g.c).
Câu 25:
Cho ∆ABC biết độ dài 3 đường trung tuyến lần lượt bằng 15; 18; 27.
a) Tính diện tích ∆ABC.
 Xem đáp án
Xem đáp án
a) Gọi M, N, P lần lượt là trung điểm của BC, AC, AB.
Giả sử AM = 15; BN = 18; CP = 27.
Khi đó ta có
Nửa chu vi ∆ABC là: .
Vậy diện tích ∆ABC là: .
Câu 26:
b) Tính độ dài các cạnh của ∆ABC.
 Xem đáp án
Xem đáp án
b) Từ kết quả câu a, ta có .
Vậy độ dài ba cạnh của ∆ABC là .
Câu 27:
Cho tam giác ABC vuông cân, . Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Từ C kẻ đường thẳng vuông góc với BE, đường thẳng đó cắt BA tại I.
a) Chứng minh BE = CI.
 Xem đáp án
Xem đáp án
a)
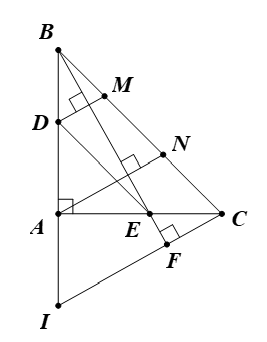
Gọi F là giao điểm của BE và CI.
Ta có (∆ABE vuông tại A) và (∆CEF vuông tại F).
Mà (cặp góc đối đỉnh).
Suy ra .
Xét ∆ABE và ∆ACI, có:
AB = AC (∆ABC vuông cân tại A);
(chứng minh trên);
.
Do đó (g.c.g).
Vậy BE = CI (cặp cạnh tương ứng).
Câu 28:
b) Qua D và A, lần lượt kẻ các đường thẳng vuông góc với BE, các đường thẳng đó cắt BC lần lượt tại M, N. Chứng minh MN = NC.
 Xem đáp án
Xem đáp án
b) Ta có (chứng minh trên).
Suy ra AE = AI (cặp cạnh tương ứng).
Mà AD = AE (giả thiết).
Do đó AD = AI.
Vì vậy A là trung điểm của DI.
Ta có DM ⊥ BE (giả thiết) và CI ⊥ BE (giả thiết).
Suy ra DM // CI.
Khi đó DMCI là hình thang.
Lại có DM ⊥ BE (giả thiết) và AN ⊥ BE (giả thiết).
Suy ra DM // AN.
Mà DM // CI (chứng minh trên).
Do đó DM // AN // CI.
Mà A là trung điểm của DI (chứng minh trên).
Suy ra AN là đường trung bình của hình thang DMCI.
Vì vậy N là trung điểm của MC.
Vậy MN = NC.
Câu 29:
Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Gọi E, F là trung điểm CA, CB. Lấy M, N, I lần lượt thuộc các đoạn SA, SC, SB. Tìm giao tuyến của:
a) (SAE) và (SBF).
 Xem đáp án
Xem đáp án
a)
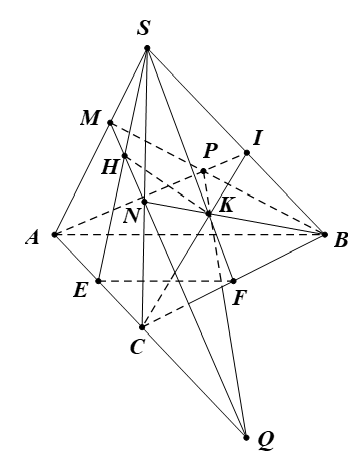
Ta có S ∈ (SAE) ∩ (SBF) (1)
Trong (ABC): C = AE ∩ BF.
Suy ra C ∈ (SAE) ∩ (SBF) (2)
Từ (1), (2), suy ra SC = (SAE) ∩ (SBF).
Câu 30:
Tìm giao tuyến của:
b) (BMN) và (SEF).
 Xem đáp án
Xem đáp án
b) Trong (SAC): gọi H = MN ∩ SE.
Suy ra H ∈ (BMN) ∩ (SEF) (3)
Trong (SBC): gọi K = BN ∩ SF.
Suy ra K ∈ (BMN) ∩ (SEF) (4)
Từ (3), (4), suy ra HK = (BMN) ∩ (SEF).
Câu 31:
Tìm giao tuyến của:
c) (CAI) và (BMN).
 Xem đáp án
Xem đáp án
c) Trong (SAB): gọi P = AI ∩ BM.
Suy ra P ∈ (CAI) ∩ (BMN) (5)
Trong (SAC): gọi Q = AC ∩ MN.
Suy ra Q ∈ (CAI) ∩ (BMN) (6)
Từ (5), (6), suy ra PQ = (CAI) ∩ (BMN).
Câu 32:
Cho tứ giác ABCD có .
a) Chứng minh 4 điểm A, B, C, D cùng nằm trên một đường tròn.
 Xem đáp án
Xem đáp án
a)
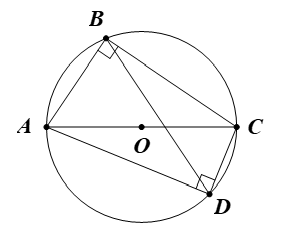
Ta có (giả thiết).
Suy ra ba điểm A, B, C cùng nằm trên một đường tròn đường kính AC (1)
Lại có (giả thiết).
Suy ra ba điểm A, D, C cùng nằm trên một đường tròn đường kính AC (2)
Từ (1), (2), suy ra bốn điểm A, B, C, D cùng nằm trên một đường tròn đường kính AC.
Câu 33:
Cho tứ giác ABCD có .
a) Chứng minh 4 điểm A, B, C, D cùng nằm trên một đường tròn.
 Xem đáp án
Xem đáp án
a)

Ta có (giả thiết).
Suy ra ba điểm A, B, C cùng nằm trên một đường tròn đường kính AC (1)
Lại có (giả thiết).
Suy ra ba điểm A, D, C cùng nằm trên một đường tròn đường kính AC (2)
Từ (1), (2), suy ra bốn điểm A, B, C, D cùng nằm trên một đường tròn đường kính AC.
Câu 34:
b) So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?
 Xem đáp án
Xem đáp án
b) Trong một đường tròn, dây lớn nhất là đường kính.
Ta thấy AC là đường kính và BD là dây cung.
Vậy AC ≥ BD.
Gọi O là trung điểm của AC.
Suy ra O là tâm của đường tròn ngoại tiếp tứ giác ABCD.
Nếu AC = BD thì BD cũng là đường kính của đường tròn ngoại tiếp tứ giác ABCD.
Suy ra O cũng là trung điểm BD.
Vậy tứ giác ABCD là hình chữ nhật.
Câu 35:
Cho đường tròn (O; R) và hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD qua M và N (M nằm giữa C và N).
1) Chứng minh rằng CM = DN.
 Xem đáp án
Xem đáp án
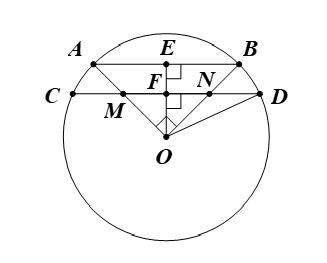
1) Kẻ OE ⊥ AB và OE cắt CD tại F.
Ta có OA = OB (giả thiết) và OM = ON (giả thiết).
Suy ra .
Áp dụng định lí Thales đảo, ta được MN // AB.
Mà OE ⊥ AB.
Do đó OE ⊥ CD tại F.
Suy ra F là trung điểm của CD (quan hệ giữa đường kính và dây cung).
Vì vậy CF = FD.
Ta có OM = ON (giả thiết).
Suy ra ∆OMN cân tại O.
∆OMN cân tại O có OF là đường cao.
Suy ra OF cũng là đường trung tuyến của ∆OMN.
Do đó F là trung điểm MN.
Vì vậy MF = NF.
Ta có CF = FD (chứng minh trên).
Khi đó CM + MF = FN + ND.
Mà MF = NF (chứng minh trên).
Vậy CM = DN.
Câu 36:
2) Giả sử . Hãy tính OM, ON theo R sao cho CM = MN = ND.
 Xem đáp án
Xem đáp án
2) ∆OMN cân tại O có .
Suy ra ∆OMN vuông cân tại O.
Mà F là trung điểm MN.
Do đó .
Ta có .
∆ODF vuông tại F: OF2 + DF2 = OD2 (Định lí Pytago).
.
⇔ 5OM2 = R2.
.
Vậy .
Câu 37:
Cho đường tròn (O; R), đường kính AB, dây cung DE. Tia DE cắt AB ở C. Biết và OC = 3R.
a) Tính độ dài CD và CE theo R.
 Xem đáp án
Xem đáp án
a)
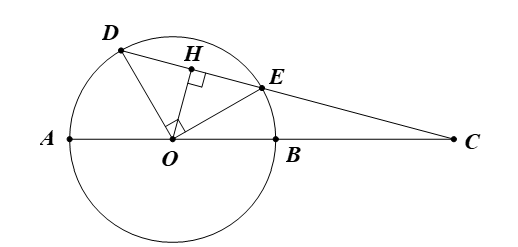
Ta có OD = OE = R và .
Suy ra ∆ODE vuông cân tại O.
Khi đó .
Kẻ OH ⊥ DE tại H.
∆ODE vuông cân tại O có OH là đường cao.
Suy ra OH cũng là đường trung tuyến của ∆ODE.
Do đó H là trung điểm của DE.
Vì vậy .
∆ODE vuông cân tại O có OH là đường cao: .
Suy ra .
Khi đó .
∆OCH vuông tại H:
Ta có .
Lại có .
Vậy và .Câu 38:
b) Chứng minh CD.CE = CA.CB.
 Xem đáp án
Xem đáp án
b) Ta có .
Mà CA.CB = (OC + OA).(OC – OB) = (3R + R).(3R – R) = 4R.2R = 8R2.
Vậy CE.CD = CA.CB (= 8R2).
Câu 39:
Cho đường tròn (O) và dây AB không đi qua tâm. Dây PQ của (O) vuông góc với AB tại H (HA > HB). Gọi M là hình chiếu vuông góc của Q trên PB; QM cắt AB tại K.
a) Chứng minh tứ giác BHQM nội tiếp và BQ > HM.
 Xem đáp án
Xem đáp án
a) Ta có (PQ ⊥ AB tại H).
Suy ra ba điểm B, H, Q cùng nằm trên một đường tròn đường kính BQ (1)
Lại có (M là hình chiếu vuông góc của Q trên PB).
Suy ra B, M, Q cùng nằm trên một đường tròn đường kính BQ (2)
Từ (1), (2), suy ra tứ giác BHQM nội tiếp đường tròn đường kính BQ.
Xét đường tròn ngoại tiếp tứ giác BHQM, ta có: BQ là đường kính và HM là dây cung.
Vậy BQ > HM.
Câu 40:
b) Chứng minh tam giác QAK cân.
 Xem đáp án
Xem đáp án
b) Ta có tứ giác BHQM nội tiếp đường tròn đường kính BQ (chứng minh trên).
Suy ra (tính chất góc ngoài).
Lại có (cùng chắn ) và (đối đỉnh).
Do đó .
Vì vậy QH là tia phân giác của .
∆AQK có QH vừa là đường cao, vừa là đường phân giác.
Vậy ∆AQK cân tại Q.
Câu 41:
c) Tia MH cắt AP tại N, từ N kẻ đường thẳng song song với AK, đường thẳng đó cắt QB tại I. Chứng minh ba điểm P, I, K thẳng hàng.
 Xem đáp án
Xem đáp án
c) Ta có (tứ giác APBQ nội tiếp (O)).
Mà (đối đỉnh).
Suy ra .
Mà (cùng chắn của đường tròn ngoại tiếp tứ giác QHBM).
Do đó .
Vì vậy tứ giác ANHQ nội tiếp đường tròn.
Suy ra (cùng chắn ).
Ta có (NI // AB và cặp góc này ở vị trí đồng vị).
Mà (cùng chắn của đường tròn (O)).
Suy ra .
Vì vậy tứ giác PNQI nội tiếp đường tròn.
Do đó (cùng chắn ).
Suy ra QI ⊥ PI (3)
∆PQK có hai đường cao PM, KH cắt nhau tại B.
Suy ra B là trực tâm của ∆PQK.
Do đó QB ⊥ PK hay QI ⊥ PK (4)
Từ (3), (4), suy ra PI ≡ PK.
Vậy ba điểm P, I, K thẳng hàng.
Câu 42:
Có 45 m vải may được 9 bộ quần áo như nhau. Hỏi phải dùng bao nhiêu m vải đó để may được 7 bộ quần áo như thế?
 Xem đáp án
Xem đáp án
Để may 1 bộ quần áo cần dùng số mét vải là:
45 : 9 = 5 (m).
Để may được 7 bộ quần áo như thế cần dùng số mét vải là:
7 × 5 = 35 (m).
Đáp số: 35m.
Câu 45:
Dấu hiệu chia hết cho 11 là gì? Có dấu hiệu chia hết cho 12 hay không?
 Xem đáp án
Xem đáp án
Dấu hiệu chia hết cho 11: Tổng các chữ số hàng lẻ – Tổng các chữ số hàng chẵn hoặc ngược lại chia hết cho 11.
Dấu hiệu chia hết cho 12: một số chia hết cho 12 khi số đó chia hết cho cả 3 và 4.
Câu 46:
Tính giá trị biểu thức bằng cách hợp lí:
a) A = x5 – 100x4 + 100x3 – 100x2 + 100x – 9 tại x = 99.
 Xem đáp án
Xem đáp án
Với x = 99, ta có: x + 1 = 99 + 1 = 100.
Ta có A = x5 – 100x4 + 100x3 – 100x2 + 100x – 9
= x5 – (x + 1)x4 + (x + 1)x3 – (x + 1)x2 + (x + 1)x – 9
= x5 – x5 – x4 + x4 + x3 – x3 – x2 + x2 + x – 9
= x – 9
= 99 – 9
= 90.
Vậy A = 90 khi x = 99.
Câu 47:
Tính giá trị biểu thức bằng cách hợp lí:
b) B = x7 – 26x6 + 27x5 – 47x4 – 77x3 + 50x2 + x – 24 tại x = 25.
 Xem đáp án
Xem đáp án
b) Với x = 25, ta có: x + 1 = 26; x + 2 = 27; 2x – 3 = 7; 3x + 2 = 77 và 2x = 50.
B = x7 – 26x6 + 27x5 – 47x4 – 77x3 + 50x2 + x – 24 tại x = 25.
= x7 – (x + 1)x6 + (x + 2)x5 – (2x – 3)x4 – (3x + 2)x3 + 2x.x2 + x – 24
= x7 – x7 – x6 + x6 + 2x5 – 2x5 + 3x4 – 3x4 – 2x3 + 2x3 + x – 24
= x – 24
= 25 – 24
= 1.
Vậy B = 1 khi x = 25.
Câu 48:
Hỏi có bao nhiêu phân số thập phân khác 0 mà tổng của mẫu số và tử số là số lẻ nhỏ nhất có tám chữ số?
 Xem đáp án
Xem đáp án
Gọi phân số thỏa mãn yêu cầu bài toán có dạng là (a, b ∈ ℕ, b ≠ 0).
Do phân số cần tìm là phân số thập phân nên b ∈ {10; 100; 1000; …}.
Theo đề, ta có tổng của mẫu số và tử số là số lẻ nhỏ nhất có tám chữ số.
Suy ra tổng của mẫu số và tử số bằng 10000001.
Khi đó 0 < a, b < 10000001.
Suy ra b ∈ {10; 100; 1000; 10000; 100000; 1000000; 10000000}.
Với b = 10, ta có: a = 10000001 – 10 = 9999991.
Với b = 100, ta có: a = 10000001 – 100 = 9999901.
Với b = 1000, ta có: a = 10000001 – 1000 = 9999001.
Với b = 10000, ta có: a = 10000001 – 10000 = 9990001.
Với b = 100000, ta có: a = 10000001 – 100000 = 9900001.
Với b = 1000000, ta có: a = 10000001 – 1000000 = 9000001.
Với b = 10000000, ta có: a = 10000001 – 10000000 = 1.
Vậy có 7 chữ số thập phân thỏa mãn yêu cầu bài toán.
Câu 49:
Tính (tính hợp lí nếu có thể):
–3752 – (29 – 3632) – 51.
 Xem đáp án
Xem đáp án
Ta có:
–3752 – (29 – 3632) – 51
= –3752 – 29 + 3632 – 51
= (–3752 + 3632) – (29 + 51)
= –120 – 80
= – 200.
Câu 50:
 Xem đáp án
Xem đáp án
Ta có (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 5050.
⇔ (x + x + x + … + x) + (1 + 2 + 3 + … + 100) = 5050.
⇔ 100x + (1 + 2 + 3 + … + 100) = 5050 (1)
Xét dãy số: 1; 2; 3; …; 100.
Số các số hạng của dãy số trên là: (100 – 1) : 1 + 1 = 100 (số hạng).
Tổng của dãy số trên là: (100 + 1) . 100 : 2 = 5050.
Từ (1), ta có: 100x + 5050 = 5050.
⇔ 100x = 0.
⇔ x = 0 : 100 = 0.
Vậy x = 0.
Câu 51:
Tìm x, biết: (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 6050.
 Xem đáp án
Xem đáp án
Ta có (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 6050.
⇔ (x + x + x + … + x) + (1 + 2 + 3 + … + 100) = 6050.
⇔ 100x + (1 + 2 + 3 + … + 100) = 6050 (1)
Xét dãy số: 1; 2; 3; …; 100.
Số các số hạng của dãy số trên là: (100 – 1) : 1 + 1 = 100 (số hạng).
Tổng của dãy số trên là: (100 + 1) . 100 : 2 = 5050.
Từ (1), ta có: 100x + 5050 = 6050.
⇔ 100x = 1000.
⇔ x = 1000 : 100 = 10.
Vậy x = 10.
Câu 52:
 Xem đáp án
Xem đáp án
Ta có (x + 1)3 – (x – 1)(x2 + x + 1) – 2 = 0.
⇔ x3 + 3x2 + 3x + 1 – (x3 – 1) – 2 = 0.
⇔ 3x2 + 3x = 0.
⇔ 3x(x + 1) = 0.
Vậy tập nghiệm của phương trình đã cho là: S = {0; –1}.
Câu 53:
Phân tích đa thức thành nhân tử: x5 – x4 + x3 – x2.
 Xem đáp án
Xem đáp án
Ta có x5 – x4 + x3 – x2 = x4.(x – 1) + x2.(x – 1)
= x2.(x – 1)(x2 + 1).
Câu 54:
Phân tích đa thức thành nhân tử: x5 – x4 – x3 – x2 – x – 2.
 Xem đáp án
Xem đáp án
Ta có x5 – x4 – x3 – x2 – x – 2 = x5 – 2x4 + x4 – 2x3 + x3 – 2x2 + x2 – 2x + x – 2
= x4.(x – 2) + x3.(x – 2) + x2.(x – 2) + x.(x – 2) + (x – 2)
= (x – 2).(x4 + x3 + x2 + x + 1).
Câu 55:
Tổng của hai số là 0,6. Thương của hai số cũng bằng 0,6. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Vì thương của hai số là 0,6 hay nên tỉ số của hai số đó là .
Số bé là: 0,6 : (3 + 5) ⨯ 3 = 0,225.
Số lớn là: 0,6 – 0,225 = 0,375.
Đáp số: Số bé là: 0,225;
Số lớn là: 0,375.
Câu 56:
Tìm y biết:
y × 1 + y × 1,5 + y × 2 + y × 2,5 + y × 3 + … + y × 5 = 94,5.
 Xem đáp án
Xem đáp án
Ta có:
y × 1 + y × 1,5 + y × 2 + y × 2,5 + y × 3 + … + y × 5 = 94,5.
y × (1 + 1,5 + 2 + 2,5 + 3 + 3,5 + 4 + 4,5 + 5) = 94,5
y × [(1 + 2 + 3 + 4 + 5) + (1,5 + 2,5 + 3,5 + 4,5)] = 94,5
y × (15 + 12) = 94,5
y × 27 = 94,5
y = 94,5 : 27
y = 3,5.
Vậy y = 3,5.
Câu 57:
Cho đa giác đều gồm 2023 cạnh. Người ta sơn các đỉnh của đa giác bằng hai màu xanh và đỏ. Chứng minh ràng tồn tại ba đỉnh được sơn cùng một màu tạo thành một đa giác cân.
 Xem đáp án
Xem đáp án
Ta có đa giác 2023 cạnh nên có 2023 đỉnh.
Do đó phải tồn tại 2 đỉnh kề nhau là P và Q đc sơn bởi cùng 1 màu – màu đỏ (Theo nguyên tắc dirichlet)
Vì đa giác đã cho là đa giác đều có số đỉnh lẻ nên phải tồn tại 1 đỉnh nào đó nằm trên đường trung trực của đoạn thẳng PQ. Giả sử đỉnh đó là A.
– Nếu A tô màu đỏ thì ta có tam giác APQ là tam giác cân có 3 đỉnh A, P, Q đc tô cùng màu đỏ.
– Nếu A tô màu xanh. Lúc đó gọi B và C là các đỉnh khác nhau của đa giác kề vs P và Q.
• Nếu cả 2 đỉnh B và C đc tô màu xanh thì tam giác ABC cân và có 3 đỉnh cùng tô màu xanh.
• Nếu ngược lại, 1 trong 2 đỉnh B và C đc tô màu đỏ thì tam giác BPQ hoặc tam giác CPQ là tam giác cân có 3 đỉnh đc tô màu đỏ.
Vậy ta có điều phải chứng minh.
Câu 58:
Bác Tư trồng lúa mì trên hai mảnh đất, cuối năm thu được 5795 kg. Mảnh đất thứ hai thu kém mảnh đất thứ nhất 1125 kg. Hỏi mảnh đất thứ hai thu được bao nhiêu yến lúa mì?
 Xem đáp án
Xem đáp án
Số kg lúa mì mảnh đất thứ hai thu được là: (5795 – 1125) : 2 = 2335 (kg).
Đổi: 2335 kg = 233,5 yến.
Đáp số: 233,5 yến lúa mì.
Câu 59:
Đường gấp khúc ABCD có AB bằng 15 cm, biết đường gấp khúc ABC dài hơn đường gấp khúc BCD là 3 cm. Tính độ dài đoạn thẳng DC.
 Xem đáp án
Xem đáp án
Ta thấy đường gấp khúc ABC và đường gấp khúc BCD có chung đoạn BC.
Mà đường gấp khúc ABC dài hơn đường gấp khúc BCD là 3cm.
Nên đoạn thẳng AB dài hơn đoạn thẳng CD là 3 cm.
Độ dài đoạn thẳng CD là: 15 – 3 = 12 (cm).
Đáp số: 12 cm.
Câu 60:
Cho các số a, b, c. Biết a là số có một chữ số, b là số có hai chữ số, c là số có ba chữ số và trung bình cộng của ba số đó là 369. Tìm số c.
 Xem đáp án
Xem đáp án
Vì trung bình cộng của ba số đó là 369 nên a + b + c = 369.3 = 1107.
Ta có:
⦁ a là số có một chữ số. Suy ra a lớn nhất là 9;
⦁ b là số có hai chữ số. Suy ra b lớn nhất là 99;
⦁ c là số có ba chữ số. Suy ra c lớn nhất là 999.
Mà 9 + 99 + 999 = 1107.
Do đó a = 9; b = 99; c = 999.
Vậy c = 999.
Câu 61:
Tìm hai số tự nhiên, biết:
a) Có tích bằng 720 và ƯCLN bằng 6.
 Xem đáp án
Xem đáp án
a) Gọi hai số tự nhiên cần tìm là a, b.
Ta có ƯCLN(a, b) = 6.
Suy ra a = 6m; b = 6n và ƯCLN(m, n) = 1.
Lại có a.b = 720.
Suy ra 6m.6n = 720.
Do đó 36m.n = 720.
Vì vậy m.n = 20.
Chọn các cặp m, n nguyên tố cùng nhau và có tích bằng 20, ta được bảng sau:
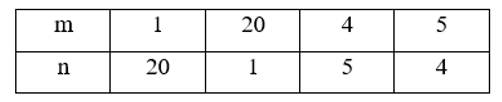
Khi đó ta có:
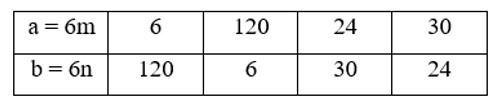
Vậy hai số tự nhiên cần tìm là 6; 120 hoặc 24; 30.
Câu 62:
Tìm hai số tự nhiên, biết:
b) Có tích bằng 4050 và ƯCLN bằng 3.
 Xem đáp án
Xem đáp án
b) Gọi hai số tự nhiên cần tìm là a, b.
Ta có ƯCLN(a, b) = 3.
Suy ra a = 6m; b = 3n và ƯCLN(m, n) = 1.
Lại có a.b = 4050.
Suy ra 3m.3n = 4050.
Do đó 9m.n = 4050.
Vì vậy m.n = 450.
Chọn các cặp m, n nguyên tố cùng nhau và có tích bằng 450, ta được bảng sau:

Khi đó ta có:

Vậy hai số tự nhiên cần tìm là 3; 1350 hoặc 6; 675 hoặc 27; 150 hoặc 54; 75.
Câu 63:
Cho tam giác ABC vuông tại A, điểm M bất kì trên cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB và AC. Tứ giác ADME là hình gì?
 Xem đáp án
Xem đáp án

Ta có tam giác ABC vuông tại A.
Suy ra .
Mà (D là chân đường vuông góc kẻ từ M đến AB) và (E là chân đường vuông góc kẻ từ M đến AC).
Do đó .
Vậy tứ giác ADME là hình chữ nhật.
Câu 64:
Tìm x, y ∈ ℕ, biết: (2x + 1)(y – 3) = 10.
 Xem đáp án
Xem đáp án
(2x + 1)(y – 3) = 10 = 1.10 = 10.1 = 2.5 = 5.2.
Ta có:
⦁ (loại vì x ∉ ℕ).
⦁ (nhận).
⦁ (loại vì x ∉ ℕ).
⦁ (nhận).
Vậy (x; y) ∈ {(0; 13), (2; 5)}.
Câu 65:
Khi cộng hai số thập phân, một học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên được kết quả là 158,6. Tìm hai số thập phân đó biết tổng đúng là 36,83.
 Xem đáp án
Xem đáp án
Tổng sai hơn tổng đúng là: 158,6 – 36,83 = 121,77.
Vì bạn học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên số thập phân đó gấp lên 100 lần.
Do đó tổng tăng lên 99 lần số thập phân đó.
Vì vậy 99 lần số thập phân đó là 121,77.
Số thập phân đó là: 121,77 : 99 = 1,23.
Số thập phân còn lại là: 36,83 – 1,23 = 35,6.
Đáp số: 1,23 và 35,6.
Câu 66:
Khi cộng hai số thập phân, một học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên được kết quả là 498,843. Tìm hai số thập phân đó biết tổng đúng là 107,793.
 Xem đáp án
Xem đáp án
Tổng sai hơn tổng đúng là: 498,843 – 107,793 = 391,05.
Vì bạn học sinh đã bỏ quên dấu phẩy của một số thập phân có hai chữ số ở phần thập phân nên số thập phân đó gấp lên 100 lần.
Do đó tổng tăng lên 99 lần số thập phân đó.
Vì vậy 99 lần số thập phân đó là 391,05.
Số thập phân đó là: 391,05 : 99 = 3,95.
Số thập phân còn lại là: 107,793 – 3,95 = 103,843.
Đáp số: 3,95 và 103,843.
Câu 67:
Một tấm vải dài 36 m. Lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài m. Lần thứ hai người ta cắt được 6 mảnh vải dài như nhau thì vừa hết tấm vải. Hỏi mỗi mảnh vải cắt ra ở lần thứ hai dài bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đổi: .
Số mét vải cắt ra lần đầu là: 1,2 . 16 = 19,2 (m)
Số mét vải cắt ra lần thứ hai là: 36 – 19,2 = 16,8 (m)
Mỗi mảnh vải cắt ra ở lần thứ hai dài số mét là: 16,8 : 6 = 2,8 (m)
Đáp số: 2,8 m.
Câu 68:
Chứng minh 4343 – 1717 chia hết cho 10.
 Xem đáp án
Xem đáp án
Ta có:
⦁ 431 = 43 có chữ số tận cùng là số 3;
⦁ 432 = 1849 có chữ số tận cùng là số 9;
⦁ 433 = 79507 có chữ số tận cùng là số 7;
⦁ 434 = 3418801 có chữ số tận cùng là số 1;
⦁ 435 = 147008443 có chữ số tận cùng là số 3.
Suy ra quy luật của nó cứ lặp đi lặp lại theo dãy bốn số 3; 9; 7; 1.
Ta thấy 43 chia 4 dư 3 nên chữ số tận cùng của 4343 là 7.
Tương tự như vậy, ta có chữ số tận cùng của 1717 là 7.
Vì vậy 4343 – 1717 ra số có chữ số tận cùng là số 0, mà số có chữ số tận cùng là số 0 thì luôn chia hết cho 10.
Vậy ta có điều phải chứng minh.
Câu 70:
Ở một nhà trẻ có một số cháu được chia thành các nhóm. Mỗi nhóm có một cô giáo phụ trách. Nếu chia mỗi nhóm 6 cháu thì có 4 cháu chưa có ai phụ trách. Nếu chia mỗi nhóm 8 cháu thì thừa một cô. Hỏi có bao nhiêu cháu và bao nhiêu cô giáo?
 Xem đáp án
Xem đáp án
Chia 1 nhóm 6 cháu thì có 4 cháu chưa có ai phụ trách.
Chia 1 nhóm 8 cháu thì thừa một cô, tức là thiếu 8 cháu để đủ cho tất cả các cô phụ trách.
Do đó ta có sơ đồ sau:
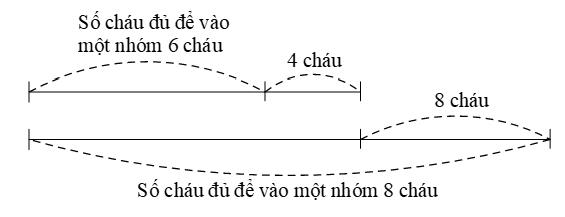
Nếu tất cả các nhóm đều có 8 cháu thì sẽ nhiều hơn nếu tất cả các nhóm đều có 6 cháu là: 4 + 8 = 12 (cháu).
Một nhóm 8 cháu nhiều hơn một nhóm 6 cháu là: 8 – 6 = 2 (cháu).
Số nhóm (hay số cô phụ trách) là: 12 : 2 = 6 (nhóm) hoặc 6 (cô).
Số cháu là: 6 ⨯ 6 + 4 = 40 (cháu) hoặc 8 ⨯ 6 – 8 = 40 (cháu).
Đáp số: 40 cháu và 6 cô.
Câu 71:
Một kho chứa 1000 bao gạo, trong đó có 350 bao gạo nếp, còn lại là các bao gạo tẻ. Hỏi:
a) Số bao gạo nếp chiếm bao nhiêu phần trăm số bao gạo trong kho?
 Xem đáp án
Xem đáp án
a) Tỉ số phần trăm số bao gạo nếp và số bao gạo trong kho là:
350 : 1000 = 0,35 = 35%.
Câu 72:
Một kho chứa 1000 bao gạo, trong đó có 350 bao gạo nếp, còn lại là các bao gạo tẻ. Hỏi:
a) Số bao gạo nếp chiếm bao nhiêu phần trăm số bao gạo trong kho?
 Xem đáp án
Xem đáp án
a) Tỉ số phần trăm số bao gạo nếp và số bao gạo trong kho là:
350 : 1000 = 0,35 = 35%.
Câu 73:
b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là bao nhiêu?
 Xem đáp án
Xem đáp án
b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là:
100% – 35% = 65%.
Đáp số: a) 35%; b) 65%.
Câu 74:
Một kho chứa 1000 bao gạo, trong đó có 450 bao gạo nếp, còn lại là các bao gạo tẻ. Hỏi:
a) Số bao gạo nếp chiếm bao nhiêu phần trăm số bao gạo trong kho?
b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là bao nhiêu?
 Xem đáp án
Xem đáp án
a) Tỉ số phần trăm số bao gạo nếp và số bao gạo trong kho là:
450 : 1000 = 0,45 = 45%.
b) Tỉ số phần trăm của số bao gạo tẻ và số bao gạo trong kho là:
100% – 45% = 55%.
Đáp số: a) 45%; b) 55%.
Câu 75:
Tìm một số thập phân có chữ số ở phần thập phân là 3. Biết rằng nếu viết thêm chữ số 2 vào trước dấu phẩy của số đó ta được một số mới gấp 9 lần số phải tìm.
 Xem đáp án
Xem đáp án
Gọi số thập phân ban đầu là: a,3 (a ∈ ℕ*)
Số thập phân mới sau khi thêm chữ số 2 vào trước dấu phẩy là a2,3.
Ta có: a,3 = a + 0,3.
a2,3 = a × 10 + 2,3 = 10 × a + 2,3.
Do số mới gấp 9 lần số phải tìm nên ta có:
10 × a + 2,3 = 9 × (a + 0,3)
10 × a + 2,3 = 9 × a + 9 × 0,3
10 × a – 9 × a = 2,7 – 2,3
a × (10 – 9) = 0,4
a = 0,4 (không thỏa mãn).
Vậy không có số nào thỏa mãn yêu cầu đề bài.
Câu 76:
Tìm giá trị của mỗi chữ số a, b, c biết rằng trong cùng một hàng thì giá trị chữ số a hơn chữ số b 2 đơn vị của hàng đó và: .
 Xem đáp án
Xem đáp án
Ta có a, b, c ∈ ℕ.
Vì a lớn hơn b 2 đơn vị nên a = b + 2.
Theo đề, ta có: .
.
.
⇒ 100a + 10b + c + 100b + 10a + c = 894.
⇒ (100a + 10a) + (10b + 100b) + (c + c) = 894.
⇒ 110a + 110b + 2c = 894.
⇒ 110 ⨯ (b + 2) + 110b = 894 – 2c.
⇒ 110b + 110 ⨯ 2 + 110b = 894 – 2c.
⇒ 110b + 110b = 894 – 220 – 2c.
⇒ 220b = 674 – 2c.
⇒ b = (674 – 2c) : 220.
Đặt phép tính, ta có:
Ở hàng phần trăm, ta thấy có hai trường hợp có thể xảy ra là c = 2 hoặc c = 7.
Với c = 2, ta có b = (674 – 2c) : 220 ≈ 3,045 không là số tự nhiên.
Vì vậy ta loại trường hợp c = 2.
Với c = 7, ta có b = (674 – 2c) : 220 = 3 là số tự nhiên.
Vì vậy ta nhận trường hợp c = 7.
Với a = b + 2, ta có a = 3 + 2 = 5.
Vậy a = 5; b = 3; c = 7 thỏa mãn yêu cầu bài toán.
