Ta có x² + 2y² + z² – 2xy – 2y – 4z + 5 = 0

⇔ x² – 2xy + y² + y² + z² – 2y + 1 + z² – 4z + 4 = 0

⇔ (x – y)² + (y – 1)² + (z – 2)² = 0

Vì (x – y)² ≥ 0 với mọi x, y

(y – 1)² ≥ 0 với mọi y

(z – 2)² ≥ 0 với mọi z

Nên (x – y)² + (y – 1)² + (z – 2)² = 0

Thay x = y, y = 1, z = 2 vào A ta có

A = (1 – 1)²⁰¹⁸ + (1 – 1)²⁰¹⁹ + (2 – 1)²⁰²⁰

A = 0 + 0 + 1

A = 1.

Ta có:

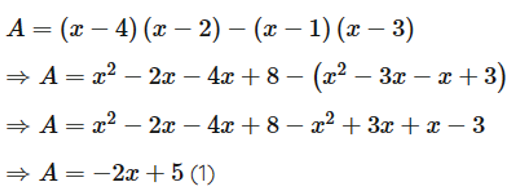
Thay $x=\frac{7}{4}$  vào (1) ta được:

$\text{A}=-2.\frac{7}{4}+5=\frac{-7}{2}+5=\frac{3}{2}$

Vậy $\text{A}=\frac{3}{2}$  .

a) A = (x + 3)² + (x – 3)(x + 3) – 2(x + 2)(x – 4)

A = (x + 3)(x + 3) + (x – 3)(x + 3) – 2[x(x – 4) + 2(x – 4)]

A = x(x + 3) + 3(x + 3) + x(x + 3) – 3(x + 3) – 2[x² – 4x + 2x – 8]

A = x² + 3x + 3x + 9 + x² + 3x – 3x – 9 – 2(x² – 2x – 8)

A = x² + 3x + 3x + 9 + x² + 3x – 3x – 9 – 2x² + 4x + 16

A = (x² + x² – 2x²) + (3x + 3x + 3x – 3x + 4x) + (9 – 9 + 16)

A = 10x + 16

Thay $x=\frac{-1}{2}$  vào A ta có

$\text{A}=10.\left(\frac{-1}{2}\right)+16=-5+16=11.$

b) B = (3x + 4)² – (x – 4)(x + 4) – 10x

B = (3x)² + 24x + 16 – (x² – 16) – 10x

B = 9x² + 24x + 16 – x² + 16 – 10x

B = (9x² – x²) + (24x – 10x) + (16 + 16)

B = 8x² + 14x + 32

Thay $\text{x}=\frac{-1}{10}$  vào B ta có

$B=8.{\left(\frac{-1}{10}\right)}^2+14.\frac{-1}{10}+32=\frac{8}{100}-\frac{7}{5}+32=\frac{767}{25}.$

c) C = (x + 1)² – (2x – 1)² + 3(x – 2)(x + 2)

C = x² + 2x + 1 – 4x² + 4x – 1 + 3(x² – 4)

C = x² + 2x + 1 – 4x² + 4x – 1 + 3x² – 12

C = (x² – 4x² + 3x²) + (2x + 4x) + (1 – 1 – 12)

C = 6x – 12

Thay x = 1 vào C ta có

C = 6 . 1 – 12 = –6.

d) D = (x – 3)(x + 3) + (x – 2)² – 2x(x – 4)

D = x² – 9 + x² – 4x + 4 – 2x² + 8x

D = (x² + x² – 2x²) + (–4x + 8x) – (9 – 4)

D = 4x – 5

Thay x = –1 vào D ta có

D = 4 . (–1) – 5 = –9.

Ta có:

$\frac{2\text{x}+2}{3}<2+\frac{x-2}{2}$

$\iff \frac{2\left(2\text{x}+2\right)}{6}<\frac{12}{6}+\frac{3\left(x-2\right)}{6}$

$\iff \frac{4\text{x}+4}{6}<\frac{12+3\text{x}-6}{6}$

⇔ 4x + 4 < 12 + 3x – 6

⇔ 4x + 4 < 6 + 3x

⇔ 4x – 3x < 6 – 4

⇔ x < 2

Vậy x < 2 là nghiệm của bất phương trình.

Ta có 60 phút = 1 giờ

Suy ra 4 phút =   $\frac{1}{15}$​giờ.

Số tự nhiên lớn nhất có 5 chữ số khác nhau là: 98 765          

Số tự nhiên nhỏ nhất có 5 chữ số khác nhau là: 10 234

Tổng của chúng là: 98 765 + 10 234 = 108 999

Vậy ổng của số tự nhiên lớn nhất có 5 chữ số khác nhau và số tự nhiên nhỏ nhất có 5 chữ số khác nhau là 108 999.

Vì 7a + 2b − 5c ⋮ 11

Nên 2(7a + 2b − 5c) ⋮ 11

Hay 14a + 4b – 10c ⋮ 11

Mà 11a + 11b + 11c ⋮ 11 và 33c ⋮ 11

Suy ra 14a + 4b – 10c – (11a + 11b + 11c) + 33c ⋮ 11

Hay 3a – 7b + 12c ⋮ 11

Vậy 3a – 7b + 12c ⋮ 11.

b) Xét ∆AHF và ∆ACH có

$\widehat{AFH}=\widehat{AHC}=90°$;

 $\widehat{CAH}$là góc chung

Suy ra $\Delta AHF\backsim \Delta ACH$  (g.g)

Do đó $\frac{AH}{AC}=\frac{AF}{AH}$

Suy ra AH² = AF . AC                         (2)

Từ (1) và (2) suy ra AE . AB = AF . AC.

c) Vì AE . AB = AF . AC nên  $\frac{A\text{E}}{AC}=\frac{AF}{AB}$

Xét ∆AFE và ∆ABC có

$\frac{A\text{E}}{AC}=\frac{AF}{AB}$ (chứng minh trên);

$\widehat{CAB}$ là góc chung

Suy ra $\Delta AFE\backsim \Delta ABC$  (c.g.c).

d) Vì $\Delta AFE\backsim \Delta ABC$  (chứng minh câu c)

Nên $\widehat{A\text{EO}}=\widehat{ACB}$   (hai góc tương ứng)

Gọi O là giao điểm của AM và FE

Xét tam giác ABC vuông tại A có AM là trung tuyến, suy ra AM = MB = MC

Do đó tam giác AMC cân tại M

Suy ra $\widehat{MAC}=\widehat{MCA}$

Mà $\widehat{A\text{EO}}=\widehat{ACB}$  , do đó $\widehat{A\text{EO}}=\widehat{O\text{AC}}$

Vì tam giác AEF vuông tại A

Nên  $\widehat{\text{AEO}}+\widehat{AFO}=90°$(trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Mà $\widehat{A\text{EO}}=\widehat{O\text{AC}}$ , suy ra $\widehat{\text{OAF}}+\widehat{AFO}=90°$

Xét tam giác AOF có

$\widehat{\text{OAF}}+\widehat{AFO}+\widehat{AOF}=180°$ (tổng ba góc trong một tam giác)

Hay $90°+\widehat{AOF}=180°$

Suy ra $\widehat{AOF}=90°$

Do đó EF ⊥ AM

Vậy EF ⊥ AM.

a)

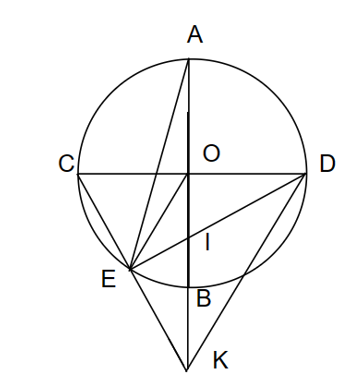
Xét (O) có AB ⊥ CD, AB và CD là hai đường kính, suy ra $\stackrel{⏜}{AC}=\stackrel{⏜}{A\text{D}}$

Mà $\widehat{CE\text{A}}$   là góc nội tiếp chắn cung $\stackrel{⏜}{AC}$

$\widehat{A\text{ED}}$ là góc nội tiếp chắn cung $\stackrel{⏜}{A\text{D}}$

Do đó $\widehat{CE\text{A}}=\widehat{A\text{ED}}$

Hay EA là phân giác của $\widehat{CE\text{D}}$ .

b) Ta có CD là đường kính, E thuộc (O) nên tam giác CED vuông tại E

Suy ra $\widehat{CE\text{D}}=90°$ . Do đó $\widehat{KE\text{D}}=90°$

Vì AB ⊥ CD nên $\widehat{DOK}=90°$

Xét tứ giác OEKD có

$\widehat{DOK}=\widehat{DEK}=90°$ (chứng minh trên)

Suy ra tứ giác OEKD nội tiếp một đường tròn.

c) Vì tam giác COK vuông tại O

Nên $\widehat{OCK}+\widehat{OKC}=90°$   (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Vì tam giác IEK vuông tại E

Nên $\widehat{EIK}+\widehat{OKC}=90°$  (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{EIK}=\widehat{OCK}$

Mà $\widehat{EIK}=\widehat{OID}$ , do đó $\widehat{OI\text{D}}=\widehat{OCK}$

Xét ∆OCK và ∆OID có

$\widehat{COK}=\widehat{I\text{OD}}\left(=90°\right)$;

$\widehat{OI\text{D}}=\widehat{OCK}$

Suy ra $\Delta OCK\backsim \Delta OI\text{D}$ (g.g)

Do đó $\frac{OC}{OI}=\frac{OK}{O\text{D}}$

Suy ra OC . OD = OI . OK

Mà OC = OD nên OD² = OI . OK

Vậy OD² = OI . OK.

Xe thứ 2 chở được số tấn gạo là: 

10,5 + 1,7 = 12,2 (tấn)

Xe thứ 3 chở được số tấn gạo là : 

12,2 + 1,1 = 13,3 (tấn)

Trung bình mỗi xe chở được số tấn gạo là:

(10,5 + 12,2 + 13,3) : 3 = 12 (tấn)

Vậy trung bình mỗi xe chở được 12 tấn gạo.

Để đếm được các hình vuông có trong hình bàn cờ mà không bỏ sót và không lặp lại, chúng ta có thể phân loại các hình vuông như sau:

Số hình vuông kích thước 1 × 1 là: 6 × 6 = 36 hình

Số hình vuông kích thước 2 × 2 là: 5 × 5 = 25 hình

Số hình vuông kích thước 3 × 3 là: 4 × 4 = 16 hình 

Số hình vuông kích thước 4 × 4 là: 3 × 3 = 9 hình

Số hình vuông kích thước 5 × 5 là: 2 × 2 = 4 hình

Số hình vuông kích thước 6 × 6 là: 1 hình

Tổng cộng: 36 + 25 + 16 + 9 + 4 + 1 = 91 hình vuông

Vậy bàn cờ có 91 hình vuông.

Gọi số cần tìm là $\overline{abc\text{d}}$

Vì $\overline{abc\text{d}}$  và a, b, c, d khác nhau

TH1: a = 6

Suy ra b ∈ {5; 7; 8; 9}

Hay b có 4 cách chọn

c có 8 cách chọn (khác a và b)

d có 7 cách chọn (khác a, b và c)

Suy ra có 1 × 4 × 7 × 8 = 224 số

TH2: a ∈ {7; 8; 9}

Khi đó b có 9 cách chọn (khác a)

c có 8 cách chọn (khác a và b)

d có 7 cách chọn (khác a, b và c)

Suy ra có 3 × 9 × 7 × 8 = 1 512 số

Vậy có 1 512 + 224 = 1 736 số thỏa mãn yêu cầu đề bài.

Vì cứ 1 giờ thì đi được 12,5 km nên

Trong 4 giờ người đó đi được số km là:

12,5 × 4 = 50 (km)

Vậy trong 4 giờ người đó đi được 50 km.

Tổng số tuổi của 3 bố con là:

19 × 3 = 57 (tuổi)

Số tuổi của bố là:

(57 + 25) : 2 = 41 (tuổi)

Tổng số tuổi của An và Hồng là:

41 – 25 = 16 (tuổi)

Số tuổi của An là :

(16 + 8) : 2 = 12 (tuổi)

Số tuổi của Hồng là:

12 – 8 = 4 (tuổi)

Vậy bố 41 tuổi, An 12 tuổi, Hồng 4 tuổi. 

Áp dụng bất đẳng thức Cô – si ta có:

$2.\frac{4}{3}\sqrt{2\text{a}+bc}\le {\left(\frac{4}{3}\right)}^2+2\text{a}+bc$

$2.\frac{4}{3}\sqrt{2b+ca}\le {\left(\frac{4}{3}\right)}^2+2b+ca$

$2.\frac{4}{3}\sqrt{2c+ab}\le {\left(\frac{4}{3}\right)}^2+2c+ab$

Suy ra

$2.\frac{4}{3}\sqrt{2\text{a}+bc}+2.\frac{4}{3}\sqrt{2b+ca}+2.\frac{4}{3}\sqrt{2c+ab}\le {\left(\frac{4}{3}\right)}^2+2\text{a}+bc+{\left(\frac{4}{3}\right)}^2+2b+ac+{\left(\frac{4}{3}\right)}^2+2c+ab$

$\iff \frac{8}{3}\left(\sqrt{2\text{a}+bc}+\sqrt{2b+ca}+\sqrt{2c+ab}\right)\le \frac{16}{3}+2\text{a}+2b+2c+ab+ac+bc$

$\iff \frac{8}{3}Q\le \frac{16}{3}+2\left(a+b+c\right)+ab+ac+bc$

$\iff \frac{8}{3}Q\le \frac{16}{3}+4+ab+ac+bc$

$\iff \frac{8}{3}Q\le \frac{28}{3}+ab+ac+bc$

Ta có

3(ab + bc + ca)

= 2(ab + bc + ca) + ab + bc + ca

≤ 2(ab + bc + ca) + a² + b² + c² = (a + b + c)² = 2² = 4

Suy ra $ab+bc+ca\le \frac{4}{3}$

Do đó $\frac{8}{3}Q\le \frac{28}{3}+\frac{4}{3}$

Hay Q ≤ 4

Dấu “ = ” xảy ra khi $\text{a}=b=c=\frac{2}{3}$

Vậy $\text{a}=b=c=\frac{2}{3}$  thì Q đạt giá trị lớn nhất bằng 4.

Vì đồ thị hàm số y = ax + b song song đường thẳng $y=\frac{1}{2}x+5$  nên $\left\{\begin{array}{l}a=\frac{1}{2}\\ b\ne 5\end{array}\right.$

Khi đó $y=\frac{1}{2}x+b$

Vì đồ thị hàm số $y=\frac{1}{2}x+b$  cắt trục hoành tại điểm có hoành độ bằng –3

Nên $0=\frac{1}{2}.\left(-3\right)+b$

Hay $b=\frac{3}{2}$

Vậy hàm số cần tìm là $y=\frac{1}{2}x+\frac{3}{2}$ .

Ta có 4(x + 5)(x + 6)(x + 10)(x + 12) = 3x²

⇔ 4(x + 5)(x + 6)(x + 10)(x + 12) – 3x² = 0

⇔ 4[(x + 5)(x + 12)][(x + 10)(x + 6)] – 3x² = 0

⇔ 4(x² + 17x + 60)(x² + 16x + 60) – 3x² = 0                    (*)

Đặt x² + 16x + 60 = a

Suy ra x² + 17x + 60 = a + x

Khi đó (*) ⇔ 4a(a + x) – 3x² = 0

⇔ 4a² + 4ax – 3x² = 0

⇔ 4a² + 4ax + x² – 4x² = 0

⇔ (2a + x)² – 4x² = 0

⇔ (2a + x – 2x)(2a + x + 2x) = 0

⇔ (2a – x)(2a + 3x) = 0

⇔ [2(x² + 16x + 60) – x][2(x² + 16x + 60) + 3x] = 0

⇔ (2x² + 32x + 120 – x)(2x² + 32x + 120 + 3x) = 0

⇔ (2x² + 31x + 120)(2x² + 35x + 120) = 0

⇔ (2x² + 16x + 15x + 120)(2x² + 35x + 120) = 0

⇔ (2x + 15)(x + 8)(2x² + 35x + 120) = 0

$\iff \left[\begin{array}{l}2\text{x}+15=0\\ x+8=0\\ 2{\text{x}}^2+35\text{x}+120=0\end{array}\right.$

$\iff \left[\begin{array}{l}\text{x=}\frac{-15}{2}\\ x=-8\\ x=\frac{-35+\sqrt{265}}{4}\\ x=\frac{-35-\sqrt{265}}{4}\end{array}\right.$

Vậy $x\in \left\{\frac{-15}{2};-8;\frac{-35+\sqrt{265}}{4};\frac{-35-\sqrt{265}}{4}\right\}$  .

Ta có:

98 + 7 – 6  + 5 – 4 + 3 – 2 – 1 = 100.

Sau khi cho số kẹo mỗi bạn là:

27 : 3 = 9 (cái)

Số kẹo của Lan ban đầu là:

9 + 5 – 1 = 13 (cái)

Số kẹo của Đào ban đầu là:

9 + 3 – 5 = 7 (cái)

Số kẹo của Hồng ban đầu là:

9 + 1 – 3 = 7 (cái)

Vậy Lan có 13 cái kẹo, Đào có 7 cái kẹo và Hồng có 7 cái kẹo.

Ta có

Vậy a + b = c thì a⁴ + b⁴ + c⁴ = 2a²b² + 2a²c² + 2b²c².

Đổi: 2 tấn 56 kg = 2 056 kg; 4 tạ 2kg = 402 kg

Thửa ruộng thứ nhất thu hoạch được số ki – lô – gam thóc là:

(2056 – 402) : 2 = 827 (kg)

Thửa ruộng thứ hai thu hoạch được số ki – lô – gam thóc là:

2056 – 827 = 1 229 (kg)

Vậy thửa ruộng thứ nhất thu hoạch được 827 kg thóc; thửa ruộng thứ hai thu hoạch được 1 229 kg thóc.

Một người sẽ làm xong trong số ngày là:

12 × 7 = 84 (ngày)

Nếu đội công nhân đó chỉ có 4 người thì đắp xong đoạn đường đó trong số ngày là:

84 : 4 = 21 (ngày)

Vậy 4 người đắp xong đoạn đường đó trong 21 ngày.

Kết quả là N = 980

Vì 980 = 2² . 5 . 7² nên số các ước của 980 là (2 + 1) . (1 + 1) . (2 + 1) = 18.

Đổi 3,6 ha = 36 000 m²

Trên cả khu đất đó có số tạ cam là:

(36 000 : 100) × 30 = 10 800 (kg)

Đổi 10 800 kg = 108 tạ

Vậy trên khu đất đó người ta thu được 108 tạ cam.

Gọi số học sinh của trường là x (x ∈ ℕ)

Theo đề bài ta có: x – 1 chia hết cho 30, 45, 50 và x chia hết cho 41

Suy ra x – 1 là BC(30, 45, 50)

Ta có:

30 = 2 . 3 . 5;

45 = 3² . 5;

50 = 2 . 5²

Suy ra BCNN(30, 45, 50) = 2 . 3² . 5² = 450 

Suy ra x – 1 ∈ {450; 900; 1 350; ...}

Hay x ∈ {451; 901; 1 351; ...}

Mà x là số có 3 chữ số

Suy ra x = 451 hoặc x = 901

Vậy trường đó có 451 học sinh hoặc 901 học sinh.

Gọi hai số tự nhiên cần tìm là a và b (a; b ∈ N ) 

Vì ƯCLN (a, b) = 36 nên a = 36m, b = 36n 

ƯCLN(m, n)  = 1 

Theo đề bài ra, ta có:

a + b = 36m + 36n = 432

Suy ra 36(m+n) = 432

Hay m + n = 12 

Suy ra ta tìm được các cặp mn thoả mãn điều kiện : 

(m; n) ∈ {(1; 11); (11; 1); (5; 7); (7; 5)}

Do đó (a; b) ∈ {(36; 396); (396; 36); (180; 252); (252; 180)}. 

Vì 145; 421; 253 chia cho x đều dư 1

Nên 144; 420; 252 chia hết cho x

Vì x lớn nhất nên x = ƯCLN(144, 420, 252)

Ta có:

144 = 2⁴ . 3²

420 = 2² . 3 . 5 . 7

252 = 2² . 3² . 7

Suy ra ƯCLN(144, 420, 252) = 2² . 3 = 12

Vậy x = 12.

Ta có:

2,6 km² + 5,87 ha + 1 300 m² + 400 000 m²

= 2 600 000 m² + 58 700 m² + 1 300 m² + 400 000 m²

= 3 060 000 m².

Ta có:

35 × 18 – 9 × 70 + 100 

= 35 × 2 × 9 – 9 × 70 + 100 

= 70 × 9 – 9 × 70 + 100

= 0 + 100

= 100.

Các số tự nhiên bé hơn 100 cần lập bao gồm các số có 1 chữ số hoặc số có hai chữ số

+) Trường hợp 1: Số thỏa mãn có 1 chữ số: Có 6 số là: 1, 2, 3, 4, 5, 6

+) Trường hợp 2: Số thỏa mãn có 2 chữ số:

Chọn chữ số hàng chục: có 6 cách chọn

Chọn chữ số hàng đơn vị: có 6 cách chọn

Suy ra có 6 × 6 = 36 số có 2 chữ số được tạo ra từ các số đã cho

Vậy có 36 + 6 = 42 số thỏa mãn yêu cầu đề bài.

Từ x > y > 0, ta có:

x > y suy ra xy > y²      (1)

x > y suy ra x² > xy      (2)

Từ (1) và (2) ta suy ra x² + xy > y² + xy hay x² > y²

Do đó x³ > xy²        (3)

Từ x > y suy ra xy² > y³              (4)

Từ (3) và (4) suy ra x³ > y³.

Vậy x³ > y³.

Nếu gọi x là số học sinh của lớp 6A thì ta có:

129 chia hết cho x và 215 chia hết cho x

Hay nói cách khác x là ước của 129 và ước của 215

Ta có 129 = 3. 43; 215 = 5. 43

Ư(129) = {1; 3; 43; 129}

Ư(215) = {1; 5; 43; 215}

Suy ra x ∈ {1; 43}. Nhưng x không thể bằng 1

Do đó x = 43

Vậy số học sinh lớp 6A là 43 học sinh.

Ta có 1 giờ 15 phút = 75 phút

Mỗi phút hai vòi nước cùng chảy vào bể được: 25 + 15 = 40 (l)

Sau 1 giờ 15 phút cả hai vòi chảy được vào bể được:

40 × 75 = 3000 (l)

Vậy sau 1 giờ 15 phút cả hai vòi đó chảy vào bể được 3000 lít nước.

Số học sinh nam của lớp đó là:

40 – 12 = 28 (học sinh)

Số học sinh nam chiếm số phần trăm với số học sinh trong lớp là:

28 : 40 × 100 = 70%

Vậy số học sinh nam chiếm 70% so với học sinh trong lớp.

Ta có 4x + 5 = 4x + 4 + 1 = 4(x + 1) + 1

Ta có 4x + 5 ⋮ x + 1

Mà 4(x + 1) ⋮ x + 1

Suy ra 1 ⋮ x + 1

Do đó x + 1 ∈ Ư(1) = {1; –1}

Suy ra x ∈ {0; –2}

Vậy x = 0, x = –2.

Đặt A = 2⁰ + 2¹ + 2² + 2³ + ... + 2ⁿ

Suy ra:

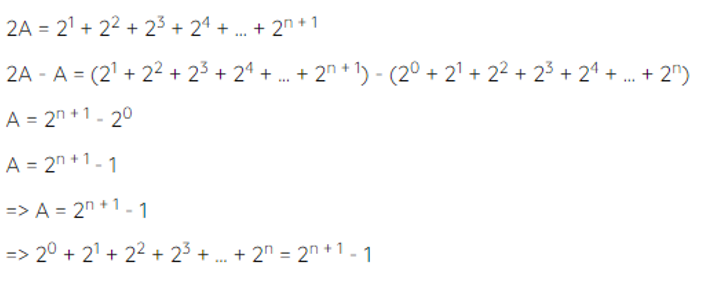
Vậy 2⁰ + 2¹ + 2² + 2³ + ... + 2ⁿ = 2ⁿ⁺¹ – 1.

Ta có:

72 : 34 = 2,11 (dư 0,26) 

13,04 : 2,05 = 6 (dư 0,74).

Ta có:

962 : 58 = 16 (dư 34).

Vì x, y, z là các số thực không âm thỏa mãn x + y + z = 1

Nên 0 ≤ x, y, z ≤ 1

Suy ra: $\left\{\begin{array}{l}{x}^2\le x\\ y^2\le y\\ z^2\le z\end{array}\right.\iff \left\{\begin{array}{l}2x^2+x+1\le x^2+2\text{x}+1\\ 2y^2+y+1\le y^2+2y+1\\ 2z^2+z+1\le z^2+2\text{z}+1\end{array}\right.\iff \left\{\begin{array}{l}2x^2+x+1\le {\left(x+1\right)}^2\\ 2y^2+y+1\le {\left(y+1\right)}^2\\ 2z^2+z+1\le {\left(\text{z}+1\right)}^2\end{array}\right.$

Suy ra $P\le \sqrt{{\left(x+1\right)}^2}+\sqrt{{\left(y+1\right)}^2}+\sqrt{{\left(z+1\right)}^2}=x+y+z+3=1+3=4$

Dấu “ = ” xảy ra khi $\left[\begin{array}{l}x=0,y=0,z=1\\ x=0,y=1,z=0\\ x=1,y=0,z=0\end{array}\right.$

Vậy P đạt giá trị lớn nhất bằng 4 khi (x; y; z) = (0; 0; 1) và các hoán vị.

Ta vẽ hình theo các bước:

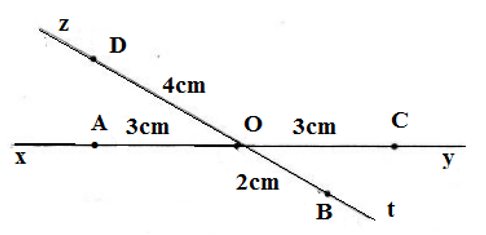
– Vẽ hai đường thẳng xy và zt cắt nhau tại O

– Trên đường thẳng xy: lấy A thuộc tia Ox, lấy C thuộc tia Oy sao cho OA = OC 3cm

– Trên đường thẳng zt:

+ Lấy B thuộc tia Ot sao cho OB = 2 cm

+ Lấy D thuộc tia Oz sao cho OD = 2OB = 2 . 2 = 4 cm.

Chiều rộng thửa ruộng là:                                                  

 $60:\frac{3}{2}=40$(m)

Diện tích là thửa ruộng là:                                                    

60 × 40 = 2400 (m²)

Trên cả thửa ruộng thu hoạch được là:          

2400 : 100 × 50 = 1200 (kg) = 12 (tạ)

Vậy thửa ruộng thu hoạch được 12 tạ thóc.

Đáp án đúng là: C

Gọi số cần lập là $\overline{\text{a}bcd\text{ef}}$

Số tự nhiên lẻ nên f có 5 cách chọn

Số cách chọn b, c, d, e là 104 cách

Gọi r là số dư khi (b + c + d + e + f) chia cho 9

Để $\overline{\text{a}bcd\text{ef}}$ chia hết cho 9 thì r + 9 phải chia hết cho 9

Mà 0 < r + a < 18 

Suy ra r + a = 9 

Hay  a = 9 – r

Do đó, a chỉ có 1 cách chọn

Suy ra số số tự nhiên lẻ có 6 chữ số và chia hết cho 9 là:

5 × 104 × 1 = 50 000

Vậy ta chọn đáp án C.

Thời gian một người ăn hết số gạo đó là:

12 × 15 = 180 (ngày)

Số người thực tế ăn hết số gạo đó là:

180 : 4 = 45 (người)

Vậy thực tế có 45 người ăn hết số gạo đó.

B = (3x + 5)(2x – 1) + (4x – 1)(3x – 2)

B = 6x² – 3x + 10x – 5 + 12x² – 8x – 3x + 2

B = 18x² – 4x – 3

Có $\left|x\right|=2\iff \left[\begin{array}{l}x=2\\ x=-2\end{array}\right.$

Thay x = 2 vào biểu thức B ta có

B = 18 . 2² – 4 . 2 – 3 = 72 – 8 – 3 = 61

Thay x = –2 vào biểu thức B ta có

B = 18 . (–2)² – 4 . (–2) – 3 = 72 + 8 – 3 = 77

Vậy B = 61 khi x = 2, B = 77 khi x = –2.

Đổi 2 m = 200 cm

Mỗi cánh cửa có số song cửa là:

(200 : 20) – 1 = 9 (song cửa)

Ngôi nhà đó có số song cửa là : 

9 × 6 = 54 (song cửa)   

Vậy ngôi nhà đó có 54 song cửa.

Người ta đã chuyển đi số tấn gạo là:

 $246,75\times \frac{4}{5}=197,4$(tấn)

Trong kho còn lại số tấn gạo là:

246,75 – 197,4 = 49,35 (tấn) = 49 350 (kg)

Vậy kho còn lại 49 350 kg gạo.

Thương của hai số là 18 dư 0,2

Tổng số bị chia, số chia, thương và dư là 103,9

Suy ra tổng của số bị chia và số chia là:

103 – (18 + 0,2) = 85,7

Số bị chia và số chia  tỉ số là 18 : 1

Nếu số bị chia giảm đi 0,2 đơn vị thì ta có phép chia hết, số bị chia gấp 18 lần số chia

Tổng của số bị chia và số chia giảm đi 0,2 đơn vị là:

85,7 – 0,2 = 85,5

Vậy số bị chia giả định là (18 phần bằng nhau, số bị chia là 1 phần)

85,5 : (18 + 1) × 18 = 81

Vậy số bị chia thật là:

81 + 0,2 = 81,2

Số chia là: 

81,2 : 19 = 4,5

Vậy số chia là 4,5 và số bị chia là 81,2.

Để có số lớn nhất thì số đó phải nhiều chữ số nhất

Suy ra mỗi chữ số đều nhỏ nhất có thể

Mà các chữ số đều khác nhau

Ta có:

17 = 0 + 1 + 2 + 3 + 4 + 7

Do đó số cần tìm là 743 210

Vậy số cần tìm là 743 210.

Ta có:

357,32 × 0,34 = 35,732 × 0,1 × 0,34

35,732 × 3,4 = 35,734 × 0, 34 × 0,1

Nên 357,32 × 0,34 = 35,732 × 3,4 

Vậy 357,32 × 0,34 = 35,732 × 3,4.

Ta có:

491,5 × 0,05 = 491,5 × 5 × 0,01

4,915 × 5 = 491,5 × 0,01 × 5

Nên 491,5 × 0,05 = 4,915 × 5

Vậy 491,5 × 0,05 = 491,5 × 5 × 0,01.