Đáp án đúng là: C

Vì H là trực tâm của tam giác ABC nên \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AH} .\overrightarrow {BC} = 0}\\{\overrightarrow {BH} .\overrightarrow {AC} = 0}\\{[\overrightarrow {AB} ,\overrightarrow {AC} ].\overrightarrow {AH} = 0}\end{array}} \right.\)

Ta giả sử \(H(x,y,z)\), ta có:

\(\begin{array}{l}\overrightarrow {BC} = (0; - 3; - 4)\\\overrightarrow {AC} = ( - 2;0; - 4)\\\overrightarrow {AH} = (x - 2;y;z)\\\overrightarrow {BH} = (x;y - 3;z)\\\overrightarrow {AB} = ( - 2;3;0)\end{array}\)

Vì \(\overrightarrow {AH} .\overrightarrow {BC} = 0 \Leftrightarrow 3y + 4z = 0\)                     (1)

Vì \(\overrightarrow {BH} \cdot \overrightarrow {AC} = 0 \Leftrightarrow x + 2z = 0\)                   (2)

Ta có: \([\overrightarrow {AB} ,\overrightarrow {AC} ] = ( - 12; - 8;6)\)

Suy ra \[\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] \cdot \overrightarrow {AH} = 0\]

\(\begin{array}{l} \Leftrightarrow - 12(x - 2) - 8y + 6z = 0\\ \Leftrightarrow - 6x - 4y + 3z + 12 = 0\end{array}\)          (3)

Từ (1), (2) và (3) ta có hệ phương trình:

\(\left\{ {\begin{array}{*{20}{l}}{3y + 4z = 0}\\{x + 2z = 0}\\{ - 6x - 4y + 3z + 12 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{{72}}{{61}}}\\{y = \frac{{48}}{{61}}}\\{z = \frac{{ - 36}}{{61}}}\end{array}} \right.\)

Suy ra \(H\left( {\frac{{72}}{{61}};\frac{{48}}{{61}};\frac{{ - 36}}{{61}}} \right)\)

Do đó \(\overrightarrow {OH} = \left( {\frac{{72}}{{61}};\frac{{48}}{{61}};\frac{{ - 36}}{{61}}} \right)\) là vecto chỉ phương của OH

Chọn \(\vec u = (6,4, - 3)\) là VTCP của OH và OH qua O(0; 0; 0) nên phương trình tham số là \(\left\{ \begin{array}{l}x = 6t\\y = 4t\\z = - 3t\end{array} \right.\)

Vậy đáp án cần chọn là C.

Ta thấy tổng 5 chữ số nhỏ nhất là 1 + 2 + 3 + 4 + 5 = 15

Tổng 5 chữ số lớn nhất là 3 + 4 + 5 + 6 + 7 =25

Do đó tổng của 5 chữ số luôn nằm nữa 15 và 25. Do đó tổng đó chia hết cho 9 nên nó chỉ có thể là 18

Mặt khác tổng của 7 chữ số là 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28

Để có được tổng 18 ta cần loại đi 2 chữ số có tổng bằng 28 – 18 = 10

Do đó có các trường hợp: loại cặp 3; 7 còn 5 số 1; 2 ; 4; 5; 6 hoặc loại cặp 4; 6 còn 5 số 1; 2; 3; 5; 7

Số số thỏa mãn là: 3 . 4! + 1 . 4! = 96 số

Vậy ta lập được 96 số.

Đáp án đúng là: C

Bất phương trình \({\rm{x}} + 5 > 0 \Leftrightarrow {\rm{x}} > - 5\)

Bất phương trình \({({\rm{x}} - 1)^2}({\rm{x}} + 5) > 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x > - 5\end{array} \right.\) nên phương án A sai

Bất phương trình \({x^2}(x + 5) > 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\{x > - 5}\end{array}} \right.\) nên phương án B sai

Bất phương trình \(\sqrt {{\rm{x}} + 5} ({\rm{x}} + 5) > 0 \Leftrightarrow {\rm{x}} > - 5\) nên phương án \({\rm{C}}\)đúng

Bất phương trình \(\sqrt {x + 5} \left( {x - 5} \right) > 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + 5 > 0}\\{x - 5 > 0}\end{array} \Leftrightarrow x > 5} \right.\) nên phương án D sai

Vậy đáp án cần chọn là C.

Đáp án đúng là: B

Phương trình \(2f(\sin x) + 3 = 0 \Leftrightarrow f(\sin x) = - \frac{3}{2}\quad (*)\) có nghiệm trên [–π; 2π]

⇔ Đường thẳng \(y = - \frac{3}{2}\) cắt đồ thị hàm số \(y = f(\sin x)\) tại các điểm trên [–π; 2π]

Đặt \(\sin x = t \Rightarrow x \in [ - \pi ;2\pi ] \Rightarrow t \in [ - 1;1]\)

Ta có bảng biến thiên:

Dựa vào bảng biến thiên ta có: đường thẳng \(y = - \frac{3}{2}\) cắt đồ thị hàm số y = f(t) tại hai điểm phân biệt

Ta có \((*) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin x = {t_1} \in (0;1)}\\{\sin x = {t_2} \in ( - 1;0)}\end{array}} \right.\)

Dựa vào đồ thị hàm số ta thấy:

+) Đường thẳng y = t₁ cắt đồ thị hàm số y = sinx tại hai điểm phân biệt trong [–π; 2π]

+) Đường thẳng y = t₁ cắt đồ thị hàm số y = sinx tại bốn điểm phân biệt trong [–π; 2π]

Như vậy đường thẳng \(y = - \frac{3}{2}\) cắt đồ thị hàm số \(y = f(\sin x)\) tại 6 điểm phân biệt trên [–π; 2π]

Suy ra phương trình đã cho có 6 nghiệm phân biệt

Vậy đáp án cần chọn là B.

Đáp án đúng là: D

Vì \(\tan \alpha = \frac{2}{3}\) nên cosα ≠ 0

Chia cả từ và mẫu của \({\rm{M}}\) cho cos³α ta được:

\(M = \frac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }} = \frac{{\frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} + 3\frac{{{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }}}}{{27\frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} - 25\frac{{{{\cos }^3}\alpha }}{{{{\cos }^3}\alpha }}}} = \frac{{{{\tan }^3}\alpha + 3}}{{27{{\tan }^3}\alpha - 25}}\)

Thay \(\tan \alpha = \frac{2}{3}\) ta được \(M = \frac{{{{\left( {\frac{2}{3}} \right)}^3} + 3}}{{27 \cdot {{\left( {\frac{2}{3}} \right)}^3} - 25}} = \frac{{ - 89}}{{459}}\)

Vậy đáp án cần chọn là D.

Đáp án đúng là: A

Vì A, B là tập hợp khác rỗng nên \(\left\{ {\begin{array}{*{20}{l}}{m - 1 < 4}\\{2m + 2 > - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 5}\\{m > - 2}\end{array}} \right.} \right. \Leftrightarrow - 2 < m < 5\)

Để \(A \cap B = \emptyset \Leftrightarrow 2m + 2 \le m - 1 \Leftrightarrow m \le - 3\) (không thỏa điều kiện –2 < m < 5)

Do đó không có giá trị nào của m để A ∩ B = ∅

Vậy với mọi \(m \in ( - 2;5)\) thì A ∩ B ≠ ∅

Phương án B sai vì học sinh không tìm điều kiện

Phương án C sai vì học sinh giải sai \(m - 1 > - 2 \Leftrightarrow m > - 1\) và kết hợp với điều kiện

Phương án D sai vì học sinh giải sai \(4 < 2m + 2 \Leftrightarrow m > 1\). Kết hợp với điều kiện

Vậy đáp án cần chọn là A.

Đáp án đúng là: D

Lấy 1 điểm A bất kì thuộc d và 1 điểm B bất kì nằm trên đường thẳng d’

Khi đó, tịnh tiến theo \(\overrightarrow {AB} \) biến đường thẳng d thành d’

Vì A; B là bất kì nên có vô số phép tịnh tiến thỏa mãn 

Vậy ta chọn đáp án D.

Đáp án đúng là: D

Theo định lí hàm sin trong tam giác OAB, ta có:

\(\frac{{OB}}{{\sin \widehat {OAB}}} = \frac{{AB}}{{\sin \widehat {AOB}}} \Leftrightarrow OB = \frac{{AB}}{{\sin \widehat {AOB}}}.\sin \widehat {OAB} = \frac{1}{{\sin 30^\circ }}.\sin \widehat {OAB} = 2\sin \widehat {OAB}\)

Do đó, độ dài OB lớn nhất khi và chỉ khi \(\sin \widehat {OAB} = 1 \Leftrightarrow \widehat {OAB} = 90^\circ \)

Khi đó \(OB = 2\sin 90^\circ = 2\)

Vậy đáp án cần chọn là D.

Đáp án đúng là: D

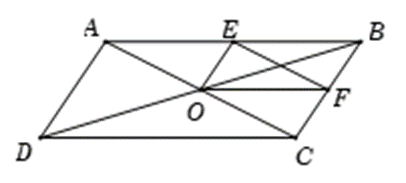
Vì ABCD là hình bình hành có O là giao điểm của hai đường chéo nên O là trung điểm của AC, BD

Xét tam giác BCD có O, F là trung điểm của BD, BC

Suy ra OF là đường trung bình

Do đó OF // CD và \(OF = \frac{1}{2}C{\rm{D}}\)

Xét tam giác BAD có O, E là trung điểm của BD, BA

Suy ra OE là đường trung bình

Do đó OE // AD và \(OE = \frac{1}{2}{\rm{AD}}\)

Ta có \(\left\{ \begin{array}{l}AB\,{\rm{//}}\,C{\rm{D}}\\OF\,{\rm{//}}\,C{\rm{D}}\end{array} \right. \Rightarrow AB\,{\rm{//}}\,{\rm{OF}}\)

\(\left\{ \begin{array}{l}AD\,{\rm{//}}\,CB\\OE\,{\rm{//}}\,A{\rm{D}}\end{array} \right. \Rightarrow CB\,{\rm{//}}\,{\rm{OE}}\)

Suy ra BEOF là hình bình hành

Do đó \(\overrightarrow {BE} + \overrightarrow {BF} = \overrightarrow {BO} \)\( \Leftrightarrow \overrightarrow {BE} + \overrightarrow {BF} - \overrightarrow {DO} = \overrightarrow {BO} - \overrightarrow {DO} = \overrightarrow {OD} - \overrightarrow {OB} = \overrightarrow {B{\rm{D}}} \)

Suy ra khẳng định D là sai

Vậy ta chọn đáp án D.

Đáp án đúng là: A

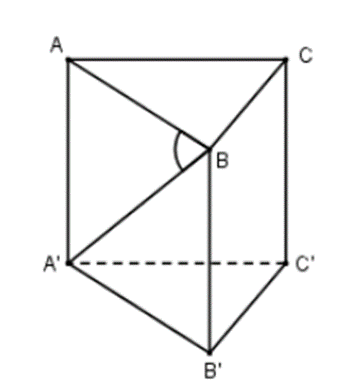
Vì \(AA' \bot (ABC)\) nên AB là hình chiếu vuông góc của A’B lên (ABC)

\(\widehat {\left( {A'B;\left( {ABC} \right)} \right)} = \left( {\widehat {A'B;AB}} \right) = \widehat {A'BA} = 30^\circ \)

Xét tam giác ABC vuông tại B có: \(AB = BC.\tan 60^\circ = a\sqrt 3 \)

Ta có AA’ ⊥ (ABC) ⊃ AB suy ra AA’ ⊥ AB

Do đó tam giác ABA’ vuông tại A

Suy ra \[{\rm{AA}}' = AB.\tan \widehat {A'BA} = a\sqrt 3 .\tan 30^\circ = a\sqrt 3 .\frac{1}{{\sqrt 3 }} = a\]

Diện tích tam giác ABC là \[{S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}a\sqrt 3 .a = \frac{{{a^2}\sqrt 3 }}{2}\]

Thể tích khối lăng trụ đứng ABC. A’B’C’ là: \(V = AA'.{S_{ABC}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}\)

Vậy đáp án cần chọn là A.

Đáp án đúng là: C

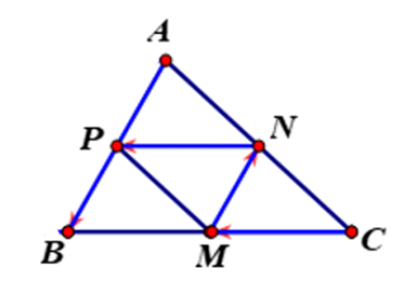
Các vectơ khác \(\overrightarrow 0 \) cùng phương với \(\overrightarrow {MN} \) là: \(\overrightarrow {NM} ,\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AP} ,\overrightarrow {PA} ,\overrightarrow {BP} ,\overrightarrow {PB} \)

Vậy ta chọn đáp án C.

Đáp án đúng là: C

Xét các trường hợp sau:

TH1: Hai học sinh lớp A đứng cạnh nhau có 2 ! . 8! cách

TH2: Giữa hai học sinh lớp A có một học sinh lớp C có \(2!.A_4^1.7!\) cách

TH3: Giữa hai học sinh lớp A có hai học sinh lớp C có \(2!.A_4^2.6!\) cách

TH4: Giữa hai học sinh lớp A có ba học sinh lớp C có \(2!.A_4^3.5!\) cách

TH5: Giữa hai học sinh lớp \({\rm{A}}\) có bốn học sinh lớp C có \(2!.A_4^4.4!\) cách

Vậy theo quy tắc cộng có \(2!\left( {8! + A_4^17! + A_4^26! + A_4^35! + A_4^44!} \right) = 145152{\rm{ }}\)cách

Vậy đáp án cần chọn là C.

Đáp án đúng là: C

Hai vectơ bằng nhau thì có độ dài bằng nhau và cùng hướng, do đó  chúng sẽ cùng phương.

Do đó, khẳng định C sai

Đáp án đúng là: D

Ta có: 7,118 + 9,52 – 8,7 + 2,21

= 16,638 – 8,7 + 2,21

= 7,938 + 2,21

= 10,148

Làm tròn 10,148 đến số thập phân thứ hai ta được 10,15

Đáp án đúng là: C

Bước 1: Coi 5 quyển sách Văn chỉ xếp vào 1 chỗ.

Bước 2: Như vậy ta sẽ xếp 5 quyển sách Văn và 7 quyển sách Toán vào 8 vị trí trên kệ sách.

Bước 3: Số cách xếp 5 quyển sách Văn là 5!

Bước 4: Số cách xếp xếp 5 quyển sách Văn và 7 quyển sách Toán trên kệ sách dài sao cho 5 quyển sách Văn xếp kề nhau là 5! . 8! cách.

Vậy đáp án cần chọn là C.

Đáp án đúng là: B

Ta có:

\(\begin{array}{l}10\pi < \alpha < 11\pi \Leftrightarrow 10\pi < \frac{\pi }{2} + k2\pi < 11\pi \\ \Leftrightarrow \frac{{19\pi }}{2} < k2\pi < \frac{{21\pi }}{2} \Leftrightarrow \frac{{19}}{4} < k < \frac{{21}}{4}\\ \Leftrightarrow k = 5\end{array}\)

Vậy đáp án cần chọn là B.

Đáp án đúng là: A

Gọi ∆ là đường thẳng cần tìm.

Gọi \(B = \Delta \cap Oy \Rightarrow B(0;t;0)\)

Ta có: (d) vuông góc với ∆ nên ta có:

\(\begin{array}{l}\overrightarrow {{u_d}} .\overrightarrow {AB} = 0 \Leftrightarrow (1; - 2;2).( - 2;t - 1; - 3) = 0\\ \Leftrightarrow - 2 - 2t + 2 - 6 = 0 \Leftrightarrow t = - 3\end{array}\)

Nên \(B(0; - 3;0);A(2;1;3)\)

Suy ra \(\overrightarrow {AB} = ( - 2; - 4; - 3)\)

Phương trình đường thẳng cần tìm có 1 vtcp là (2; 4; 3) và đi qua điểm B(0; –3; 0) dạng: \(\left\{ \begin{array}{l}x = 2t\\y = - 3 + 4t\\z = 3t\end{array} \right.\)

Vậy đáp án cần chọn là A.

Đáp án đúng là B

Vì với mọi x ∈ ℝ ta có –1 ≤ cos2x ≤ 1 nên tập giá trị của hàm số y = cos2x là [–1; 1]

Vậy ta chọn đáp án B.

Ta có:

\(\begin{array}{l}\overrightarrow {AB} = \left( {2; - 4} \right)\\\overrightarrow {AC} = \left( { - 1;2} \right)\end{array}\)

Ta thấy \(\overrightarrow {AC} = - \frac{1}{2}\overrightarrow {AB} \)

Suy ra có phép vị tự tâm A, tỉ số \(\frac{{ - 1}}{2}\) biến điểm B thành điểm C

Vậy \(k = \frac{{ - 1}}{2}\).

Đáp án đúng là: A

+ Trường hợp 1: Tam giác đươc tạo ra có 2 điểm thuộc đường thẳng a và 1 điểm thuộc đường thẳng b

Có:  10 . 9 = 90 cách chọn 2 điểm thuộc đường thẳng a

Và có 8 cách chọn  1 điểm thuộc đường thẳng b

Trong trường hợp này có:  90 . 8 = 720 cách

+ Trường hợp 2:  Tam giác được tạo thành có 1 điểm thuộc a và 2 điểm thuộc đường thẳng b

Có 10 cách chọn 1 điểm thuộc a

Và 8 . 7 = 56 cách chọn 2 điểm thuộc b

Trong trường hợp này có: 10 . 56 = 560 cách

Theo quy tắc cộng có:  720 +  560 = 1280 tam giác

Vậy ta chọn đáp án A.

Đáp án đúng là: A

Điều kiện x > 0. Ta có:

\(\begin{array}{l}{\left[ {{{\log }_{\frac{1}{3}}}(9x)} \right]^2} + {\log _3}\frac{{{x^2}}}{{81}} - 7 = 0\\ \Leftrightarrow {\left( {2 + {{\log }_3}x} \right)^2} + 2{\log _3}x - 4 - 7 = 0\\ \Leftrightarrow \log _3^2x + 6{\log _3}x - 7 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\log }_3}x = 1}\\{{{\log }_3}x = - 7}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = {3^{ - 7}}}\end{array} \Rightarrow P = {3^{ - 6}} = \frac{1}{{{9^3}}}} \right.\end{array}\)

Vậy ta chọn đáp án A.

Đáp án đúng là: D

Giả sử chia số 120 thành bốn phần x, y, z, t tỉ lệ với các số 2; 4; 6; 8

Khi đó ta có \(:\frac{x}{2} = \frac{y}{4} = \frac{z}{8} = \frac{t}{{10}}\) và \(x + y + z + t = 120\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được :

\(\frac{x}{2} = \frac{y}{4} = \frac{z}{8} = \frac{t}{{10}} = \frac{{x + y + z + t}}{{2 + 4 + 8 + 10}} = \frac{{120}}{{24}} = 5\)

Do đó:

\(\begin{array}{l}\frac{x}{2} = 5 \Rightarrow x = 5.2 = 10\\\frac{y}{4} = 5 \Rightarrow y = 5.4 = 20\\\frac{z}{8} = 5 \Rightarrow z = 5.8 = 40\\\frac{t}{{10}} = 5 \Rightarrow t = 5.10 = 50\end{array}\)

Suy ra các số cần tìm sắp xếp theo thứ tự tăng dần là 10; 20; 40; 50

Vậy ta chọn đáp án D.

Đáp án đúng là: B

Số tổ hợp chập 9 của 9 phần tử là \(C_9^9\)

Vậy đáp án cần chọn là B.

Đáp án đúng là: D

Phương trình hoành độ giao điểm của (P) và Ox là: x² – 4x + m = 0     (1)

Để (P) cắt Ox tại hai điểm phân biệt x₁; x₂

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{a \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4 - m > 0}\\{1 \ne 0}\end{array} \Leftrightarrow m < 4} \right.} \right.\)

Giả sử \(A\left( {{x_1};0} \right),B\left( {{x_2};0} \right)\)

Theo định lí Vi – ét có: \({x_1} + {x_2} = 4,{x_1}{x_2} = m\)

Ta có \(OA = 3OB \Leftrightarrow \left| {{x_1}} \right| = 3\left| {{x_2}} \right| \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_1} = 3{x_2}}\\{{x_1} = - 3{x_2}}\end{array}} \right.\)

Trường hợp 1: \({x_1} = 3{x_2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = 3}\\{{x_2} = 1}\end{array} \Rightarrow m = 3} \right.\) (thỏa mãn)

Trường hợp 2: \({x_1} = - 3{x_2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = 6}\\{{x_2} = - 2}\end{array} \Rightarrow m = - 12} \right.\) (thỏa mãn)

Vậy \(S = - 12 + 3 = - 9\)

Vậy đáp án cần chọn là D.

Đáp án đúng là: A

Nhìn vào đồ thị ta xét phương trình \(f(x) = - 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 1}\end{array}} \right.\)

Suy ra:

\(f(\cos x) = - 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 1}\\{\cos x = - 1}\end{array} \Leftrightarrow x = k\pi \quad (k \in \mathbb{Z})} \right.\)

Đề phương trình có nghiệm thuộc đoạn [0; 2π] thì \(0 \le k\pi \le 2\pi \Leftrightarrow 0 \le k \le 2\)

Mà \(k \in \mathbb{Z} \Rightarrow k \in \{ 0;1;2\} \)

Suy ra phương trình đã cho có 3 nghiệm thuộc khoảng [0; 2π]

Vậy ta chọn đáp án A.

Đáp án đúng là: C

Hàm số xác định khi \(x - 2m + 1 \ne 0 \Leftrightarrow x \ne 2m - 1\)

Do đó hàm số \(y = \frac{{x + 1}}{{x - 2m + 1}}\) xác định trên [0; 1) khi:

\(\left[ {\begin{array}{*{20}{l}}{2m - 1 < 0}\\{2m - 1 \ge 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{1}{2}}\\{m \ge 1}\end{array}} \right.} \right.\)

Vậy đáp án đúng là C.

Đáp án đúng là: B

Đặt \(\left\{ \begin{array}{l}u = \ln \left( {2{\rm{x}} + 1} \right)\\dv = x{\rm{dx}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{2}{{2{\rm{x}} + 1}}d{\rm{x}}\\v = \frac{{{x^2} - \frac{1}{4}}}{2} = \frac{{\left( {2{\rm{x}} + 1} \right)\left( {2{\rm{x}} - 1} \right)}}{8}\end{array} \right.\)

\( \Rightarrow I = \left. {\left[ {\frac{{4{{\rm{x}}^2} - 1}}{8}\ln \left( {2{\rm{x}} + 1} \right)} \right]} \right|_0^4 - \int\limits_0^4 {\frac{{2{\rm{x}} - 1}}{4}} {\rm{dx}}\)

\( \Rightarrow I = \frac{{63}}{8}\ln 9 = \left. {\frac{{\left( {{x^2} - 4} \right)}}{4}} \right|_0^4 = \frac{{63}}{4}\ln 3 - 3 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 63}\\{b = 4}\\{c = 3}\end{array} \Rightarrow S = a + b + c = 70} \right.\)

Vậy ta chọn đáp án C.

Đáp án đúng là: B

Tập xác định D = ℝ \ {1}

Ta có \(y' = \frac{{ - 14}}{{{{\left( {x - 1} \right)}^2}}} < 0;\forall x \in D\)

Suy ra hàm số nghịch biến trên (–∞; 1) và (1; +∞)

Vậy ta chọn đáp án B.

Đáp án đúng là: B

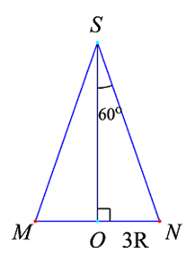
Thiết diện qua trục là tam giác SMN \( \Rightarrow \widehat {MSN} = 120^\circ \Rightarrow \widehat {OSN} = 60^\circ \)

Ta có: \(SO = \frac{{ON}}{{\tan 60^\circ }} = \frac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)

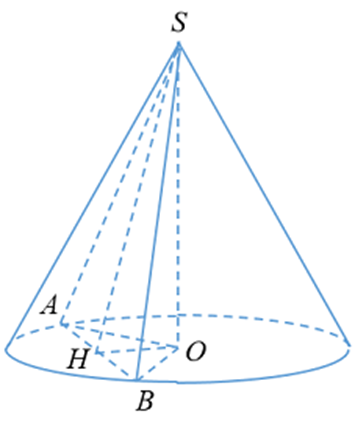
Vì (SAB) tạo với đáy góc 60°\( \Rightarrow \widehat {SHO} = 60^\circ \)

Ta có: \(OH = \frac{{SO}}{{\tan 60^\circ }} = \frac{{R\sqrt 3 }}{{\sqrt 3 }} = R\)

Vì tam giác SOH vuông tại O nên

\({\rm{S}}{O^2} + O{H^2} = S{H^2} \Leftrightarrow {(R\sqrt 3 )^2} + {R^2} = S{H^2} \Leftrightarrow SH = 2R\)

Vì tam giác BOH vuông tại H nên

\(O{H^2} + H{B^2} = O{B^2} \Leftrightarrow H{B^2} = {(3R)^2} - {R^2} \Leftrightarrow HB = 2R\sqrt 2 \)

\( \Rightarrow AB = 2HB = 4R\sqrt 2 \)

Ta có: \({S_{SAB}} = \frac{1}{2}.SH.AB = \frac{1}{2}.2R.4R\sqrt 2 = 4\sqrt 2 .{R^2}\)

Vậy ta chọn đáp án B.

Đáp án đúng là: A

Khi quay hình chữ nhật ABCD quanh cạnh AB ta được khối trụ có chiều cao h = AB = 4, bán kính đáy r = AD = 3

Vậy thể tích khối trụ là V = πr²h = π . 3² . 4 = 36π

Vậy đáp án cần chọn là A.

Đáp án đúng là: B

Do I là trung điểm AD nên \(IA = I{\rm{D}} = \frac{{A{\rm{D}}}}{2} = \frac{{3{\rm{a}}}}{2}\)

Ta có: \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {I{\rm{D}}} = \left( {\overrightarrow {IA} + \overrightarrow {IA} + \overrightarrow {AB} } \right).\overrightarrow {I{\rm{D}}} = 2\overrightarrow {IA} .\overrightarrow {I{\rm{D}}} = \frac{{ - 9{{\rm{a}}^2}}}{2}\)

Vậy đáp án cần chọn là B.

Đáp án đúng là: D

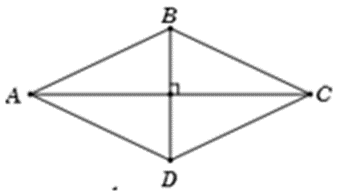
Gọi \(O = AC \cap BD\), giả thiết không cho góc, ta phân tích các vec tơ \(\overrightarrow {AB} ;\overrightarrow {AC} \) theo các vec tơ có giá vuông góc với nhau

Ta có:

\(\overrightarrow {AB} .\overrightarrow {AC} = (\overrightarrow {AO} + \overrightarrow {OB} ).\overrightarrow {AC} = \overrightarrow {AO} .\overrightarrow {AC} + \overrightarrow {OB} .\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AC} + 0 = \frac{1}{2}A{C^2} = 32\)

Vậy đáp án cần chọn là D.

Đáp án đúng là: A

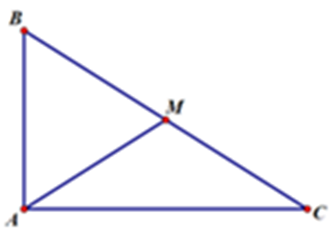
Ta có: \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{a^2}}}{2}\)

\(\begin{array}{l} \Leftrightarrow \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )(\overrightarrow {AC} + \overrightarrow {AB} ) = \frac{{{a^2}}}{2}\\ \Leftrightarrow A{C^2} - A{B^2} = {a^2}\end{array}\)

Mặt khác, tam giác \({\rm{ABC}}\) vuông tại A nên \(A{B^2} + A{C^2} = 3{a^2}\)

Suy ra \(\left\{ {\begin{array}{*{20}{c}}{A{C^2} = 2{a^2}}\\{A{B^2} = {a^2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{AC = a\sqrt 2 }\\{AB = a}\end{array}} \right.} \right.\)

Vậy ta chọn đáp án A.

Đáp án đúng là: B

Gọi G là trọng tâm của tam giác ABC

Ta có: \(2\overrightarrow {{\rm{MA}}} + 3\overrightarrow {{\rm{MB}}} + 4\overrightarrow {{\rm{MC}}} \)\( = 2(\overrightarrow {{\rm{MI}}} + \overrightarrow {{\rm{IA}}} ) + 3(\overrightarrow {{\rm{MI}}} + \overrightarrow {{\rm{IB}}} ) + 4(\overrightarrow {{\rm{MI}}} + \overrightarrow {{\rm{IC}}} )\)

Chọn điểm I sao cho

\(2\overrightarrow {{\rm{IA}}} + 3\overrightarrow {{\rm{IB}}} + 4\overrightarrow {{\rm{IC}}} = \vec 0 \Leftrightarrow 3(\overrightarrow {{\rm{IA}}} + \overrightarrow {{\rm{IB}}} + \overrightarrow {{\rm{IC}}} ) + \overrightarrow {{\rm{IC}}} - \overrightarrow {{\rm{IA}}} = \vec 0\)

Mà G là trọng tâm của tam giác ABC

\( \Rightarrow \overrightarrow {{\rm{IA}}} + \overrightarrow {{\rm{IB}}} + \overrightarrow {{\rm{IC}}} = 3\overrightarrow {{\rm{IG}}} \)

Khi đó: \(9\overrightarrow {{\rm{IG}}} + \overrightarrow {{\rm{IC}}} - \overrightarrow {{\rm{IA}}} = \vec 0 \Leftrightarrow 9\overrightarrow {{\rm{IG}}} + \overrightarrow {{\rm{AI}}} + \overrightarrow {{\rm{IC}}} = \vec 0 \Leftrightarrow 9\overrightarrow {{\rm{IG}}} = \overrightarrow {{\rm{CA}}} {\rm{                 }}(*)\)

Do đó, \(\left| {2\overrightarrow {{\rm{MA}}} + 3\overrightarrow {{\rm{MB}}} + 4\overrightarrow {{\rm{MC}}} } \right| = \left| {\overrightarrow {{\rm{MB}}} - \overrightarrow {{\rm{MA}}} } \right|\)

\[\begin{array}{l} \Leftrightarrow \left| {9\overrightarrow {{\rm{MI}}} + 2\overrightarrow {{\rm{IA}}} + 3\overrightarrow {{\rm{IB}}} + 4\overrightarrow {{\rm{IC}}} } \right| = \left| {\overrightarrow {{\rm{AB}}} } \right|\\ \Leftrightarrow 9{\rm{MI}} = {\rm{AB}}\end{array}\]

Vì I là điểm cố định thỏa mãn (*) nên tập hợp các điểm M cần tìm là đường tròn tâm I, bán kính \[{\rm{R}} = \frac{{AB}}{9} = \frac{a}{9}\] 

Vậy đáp án cần chọn là B.

Đáp án đúng là: A

Ta có tam giác đều ABC nên \(\overrightarrow {AB} ;\overrightarrow {BC} \) không cùng hướng 

Suy ra \(\overrightarrow {AB} \ne \overrightarrow {BC} \)

Do đó A sai, B đúng và C, D cũng đúng

Vậy đáp án cần chọn là A.

Đáp án đúng là: C

Ta có thể thấy: \( - 10\overrightarrow a - 2\overrightarrow b = - 2\left( {5\overrightarrow a + \overrightarrow b } \right)\)

Như vậy\(5\overrightarrow a + \overrightarrow b \) và\( - 10\overrightarrow a - 2\overrightarrow b \) là cặp vectơ cùng phương

Vậy đáp án cần chọn là C.

Đáp án đúng là: B

Gọi số thỏa mãn bài toán là abc

Có 3 cách chọn chữ số a

Có 3 cách chọn chữ số b

Có 3 cách chọn chữ số c

Suy ra có 3 . 3 . 3 = 27 số tạo thành từ các chữ số 3, 2, 1

Vậy đáp án cần chọn là B.

Đáp án đúng là: D

Ta có:

\(\begin{array}{l}y = \frac{{x - {m^2}}}{{x + 8}},x \ne - 8\\ \Rightarrow y' = \frac{{1.8 - 1.\left( { - {m^2}} \right)}}{{{{(x + 8)}^2}}} = \frac{{{m^2} + 8}}{{{{(x + 8)}^2}}} > 0,\forall x \ne - 8\end{array}\)

Suy ra hàm số luôn đồng biến trên các khoảng (–∞;–8) và (–8; +∞)

\( \Rightarrow {\min _{[0;3]}}y = y(0) = - \frac{{{m^2}}}{8} = - 2 \Rightarrow m = \pm 4\)

Suy ra |m| < 5

Vậy đáp án cần chọn là D.

Đáp án đúng là: D

4^x – m . 2^x – m + 15 ≥ 0 (1)

Đặt \({2^x} = t(t > 0)\) ta được \({t^2} - mt - m + 15 \ge 0\)      (2)

Để bất phương trình (1) có nghiệm đúng với mọi x ∈ [1; 2] thì (2) đúng với mọi t ∈ [2; 4]

Ta có: \((2) \Leftrightarrow {t^2} + 15 \ge m(t + 1) \Leftrightarrow \frac{{{t^2} + 15}}{{t + 1}} \ge m\)

Xét hàm số \(f(t) = \frac{{{t^2} + 15}}{{t + 1}},t \in [2;4]\)

Ta có \(f'(t) = \frac{{(t + 5)(t - 3)}}{{{{(t + 1)}^2}}}\); \(f'(t) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = - 5\end{array} \right. \Leftrightarrow t = 3\)

Bảng biến thiên:

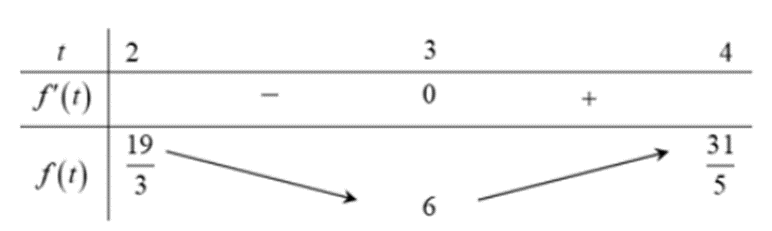
Suy ra m ≤ 6

Vậy ta chọn đáp án D.

Đáp án đúng là: D

Ta có ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi các vec tơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng phương, hay \(\exists k \in \mathbb{R},k \ne 0\) sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \) hoặc \(\overrightarrow {AC} = k\overrightarrow {BC} \)

Chú ý rằng hệ số k phải khác 0 nên chỉ có đáp án D sai

Vậy đáp án cần chọn là D.

Đáp án đúng là: A

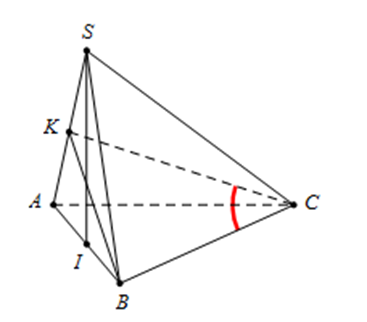
Gọi I là trung điểm của AB

Vì tam giác SAB đều nên \(\left\{ {\begin{array}{*{20}{l}}{SI = \frac{{a\sqrt 3 }}{2}}\\{SI \bot AB}\end{array}} \right.\)

Mà \((SAB) \bot (ABC) \Rightarrow SI \bot (ABC){\rm{; }}\left\{ {\begin{array}{*{20}{l}}{SI \bot AC}\\{AB \bot AC}\end{array} \Rightarrow AC \bot (SAB)} \right.\)

Kẻ BK vuông góc với SA tại K

Vì \(AC \bot (SAB)\) nên \(AC \bot BK \Rightarrow BK \bot (SAC){\rm{ v\`a }}BK = \frac{{a\sqrt 3 }}{2}\)

Do đó, góc giữa BC và (SAC) là \(\widehat {BCK}\) suy ra \(\widehat {BCK} = 30^\circ \)

Khi đó: \(BC = \frac{{BK}}{{\sin \widehat {BCK}}} = a\sqrt 3 \)

Vì tam giác ABC vuông tại A nên theo định lý Pytago có \(AC = \sqrt {B{C^2} - A{B^2}} = a\sqrt 2 \)

Suy ra diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}.AB.AC = \frac{{{a^2}\sqrt 2 }}{2}\)

Vậy ta chọn đáp án A.

Đáp án đúng là: A

Ta có:

\(\int_1^2 {\frac{{x + 1}}{{{x^2} + x\ln x}}} \;{\rm{d}}x = \int_1^2 {\frac{{1 + \frac{1}{x}}}{{x + \ln x}}} \;{\rm{d}}x = \int_1^2 {\frac{{{\rm{d}}(x + \ln x)}}{{x + \ln x}}} = \ln |x + \ln x|_1^2 = \ln (\ln 2 + 2)\)

Mặt khác:

\(\begin{array}{l}\int_1^2 {\frac{{x + 1}}{{{x^2} + x\ln x}}} \;{\rm{d}}x = \ln (\ln a + b) = \ln (\ln 2 + 2)\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 2}\end{array} \Rightarrow P = 12} \right.\end{array}\)

Vậy đáp án cần chọn là A.

Đáp án đúng là: D

Ta có: log_ab > log_aa = 1, log_ba < log_bb = 1

Suy ra log_ba < 1 < log_ab

Vậy ta chọn đáp án D.

Đáp án đúng là: C

Giả sử \(w = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\). Ta có:

\(\begin{array}{l}w = (3 + 4i)z + i \Leftrightarrow a + bi = (3 + 4i)z + i\\ \Leftrightarrow a + (b - 1)i = (3 + 4i)z\\ \Leftrightarrow z = \frac{{a + (b - 1)i}}{{3 + 4i}}\\ \Leftrightarrow z = \frac{{[a + (b - 1)i](3 - 4i)}}{{25}}\\ \Leftrightarrow z = \frac{1}{{25}}[3a + 4b - 4 + ( - 4a + 3b - 3)i]\end{array}\)

Theo giả thiết cho |z| = 4 nên ta có

\(\begin{array}{l}\frac{1}{{{{25}^2}}}\left[ {{{(3a + 4b - 4)}^2} + {{( - 4a + 3b - 3)}^2}} \right] = {4^2}\\ \Leftrightarrow {(3a + 4b - 4)^2} + {( - 4a + 3b - 3)^2} = {100^2}\\ \Leftrightarrow 25{a^2} + 25{b^2} + 25 - 50b = {100^2}\\ \Leftrightarrow {a^2} + {b^2} - 2b + 1 = {20^2}\\ \Leftrightarrow {a^2} + {(b - 1)^2} = {20^2}\end{array}\)

Tập hợp các điểm trong mặt phẳng tọa độ Oxy biểu diễn số phức w là một đường tròn có bán kính bằng 20

Vậy ta chọn đáp án C.

Đáp án đúng là: D

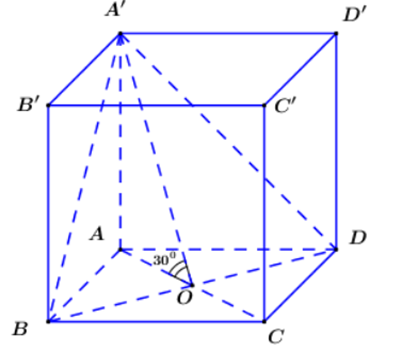
Ta có:

(A’BC) ∩ (ABCD) = BD

\(\left\{ \begin{array}{l}AA' \bot B{\rm{D}}\\AO \bot B{\rm{D}}\end{array} \right. \Rightarrow \left( {A'AO} \right) \bot B{\rm{D}}\)

\(\left\{ \begin{array}{l}\left( {A'AO} \right) \cap \left( {A'B{\rm{D}}} \right) = A'O\\\left( {A'AO} \right) \cap \left( {ABC{\rm{D}}} \right) = AO\end{array} \right.\)

Suy ra: \(\widehat {\left( {\left( {A'B{\rm{D}}} \right);\left( {ABC{\rm{D}}} \right)} \right)} = \widehat {\left( {A'O,AO} \right)} = \widehat {AO{\rm{A}}'} = 30^\circ \)

Vì ABCD là hình vuông có hai đường chéo cắt nhau tại O

Suy ra O là trung điểm của AC và BD

Do đó \(AO = \frac{1}{2}AC = \frac{1}{2}B{\rm{D}} = a\)

Xét tam giác A’OA vuông tại A có \(AA' = \tan 30^\circ .AO = \frac{{a\sqrt 3 }}{3}\)

\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABC{\rm{D}}}}{\rm{.AA}}' = \frac{1}{2}AC.B{\rm{D}}.AA' = \frac{1}{2}.{(2a)^2} \cdot \frac{{a\sqrt 3 }}{3} = \frac{{2\sqrt 3 {a^3}}}{3}\)

Vậy ta chọn đáp án D.

Đáp án đúng là: B

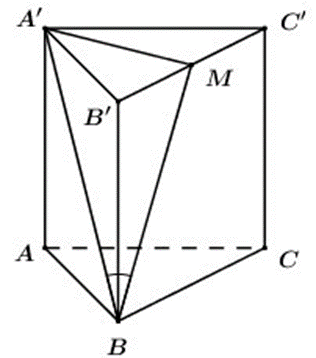
Gọi M là trung điểm của B’C’

Vì tam giác A’B’C’ đều nên A’M ⊥ B’C

Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right. \Rightarrow A'M \bot \left( {BCC'B'} \right)\)

\( \Rightarrow \widehat {\left( {A'B;\left( {BCC'B'} \right)} \right)} = \widehat {\left( {A'B;MB} \right)} = \widehat {A'BM} = 30^\circ \)

Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh a có AM là đường cao nên \(A'M = \frac{{a\sqrt 3 }}{2}\) và \({S_{A'B'C'}} = \frac{1}{2}.AM.B'C' = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^2}\sqrt 3 }}{4}\)

Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) nên tam giác A’BM vuông tại M

Suy ra: \(BM = A'M.\cot 30^\circ = \frac{{3a}}{2}\)

Áp dụng định lí Pythagore trong tam giác vuông BB’M ta có:

\(BB' = \sqrt {B{M^2} - B'{M^2}} = \sqrt {{{\left( {\frac{{3a}}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}} = a\sqrt 2 \)

Do đó \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 6 }}{4}.\)

Vậy đáp án cần chọn là B.

Đáp án đúng là: D

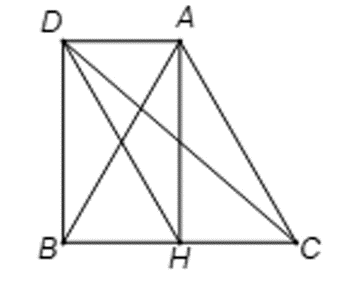
Gọi D là điềm thỏa mãn tứ giác ACHD là hình bình hành

Suy ra AD = HC, AD // HC

Mà BH = HC, AH ⊥ BC (do tam giác ABC đều có trung tuyến AH)

Do đó AHBD là hình chữ nhật

Suy ra \(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD\)

Vì tam giác BCD vuông tại B nên theo định lý Pytago ta có:

\(CD = \sqrt {B{D^2} + B{C^2}} = \sqrt {A{H^2} + B{C^2}} = \sqrt {\frac{{3{a^2}}}{4} + {a^2}} {\rm{ }} = \frac{{a\sqrt 7 }}{2}\)

Vậy ta chọn đáp án D.