Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB = a, đường thẳng A’B tạo với mặt phẳng (BCC’B’) một góc bằng 30°. Tính thể tích khối lăng trụ ABC.A’B’C’.
A. \(\frac{{3{{\rm{a}}^3}}}{2}\)
B. \(\frac{{{{\rm{a}}^3}\sqrt 6 }}{4}\)
C. \(\frac{{3{{\rm{a}}^3}}}{4}\)
D. \(\frac{{\sqrt 3 {{\rm{a}}^3}}}{4}\).
Giải bởi Vietjack
Đáp án đúng là: B
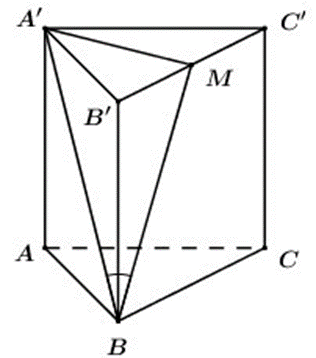
Gọi M là trung điểm của B’C’
Vì tam giác A’B’C’ đều nên A’M ⊥ B’C
Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right. \Rightarrow A'M \bot \left( {BCC'B'} \right)\)
\( \Rightarrow \widehat {\left( {A'B;\left( {BCC'B'} \right)} \right)} = \widehat {\left( {A'B;MB} \right)} = \widehat {A'BM} = 30^\circ \)
Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh a có AM là đường cao nên \(A'M = \frac{{a\sqrt 3 }}{2}\) và \({S_{A'B'C'}} = \frac{1}{2}.AM.B'C' = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^2}\sqrt 3 }}{4}\)
Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) nên tam giác A’BM vuông tại M
Suy ra: \(BM = A'M.\cot 30^\circ = \frac{{3a}}{2}\)
Áp dụng định lí Pythagore trong tam giác vuông BB’M ta có:
\(BB' = \sqrt {B{M^2} - B'{M^2}} = \sqrt {{{\left( {\frac{{3a}}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}} = a\sqrt 2 \)
Do đó \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 6 }}{4}.\)
Vậy đáp án cần chọn là B.
Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, BD = 2a, góc giữa hai mặt phẳng (A′BD) và (ABCD) bằng 30°. Thể tích của khối hộp chữ nhật đã cho bằng:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi E, F lần lượt là trung điểm của AB, BC. Đẳng thức nào sau đây sai?
Cho hình thoi ABCD có AC = 8 và BD = 6. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
Cho hàm số f(x) có bảng biến thiên như sau:
![Số nghiệm thuộc đoạn [-pi; 2pi] của phương trình 2f(sinx) + 3 = 0 là: A. 4 B. 6 C. 3 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid12-1695110777.png)
Số nghiệm thuộc đoạn [–π; 2π] của phương trình 2f(sinx) + 3 = 0 là:
Cho hai học sinh lớp A, ba học sinh lớp B và bốn học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh nào lớp B. Hỏi có bao nhiêu cách xếp hàng như vậy?
Cho hàm số y = f(x) có bảng biến thiên như sau:
![Số nghiệm thuộc đoạn [0; 2pi] của phương trình f(cosx) = -2 là: A. 3 B. 0 C. 2 D. 1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid18-1695111629.png)
Số nghiệm thuộc đoạn [0; 2π] của phương trình f(cosx) = –2 là:
Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức \(\left| {2\overrightarrow {MA} + 3\overrightarrow {MB} + 4\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB} - \overrightarrow {MA} } \right|\) là đường tròn cố định có bán kính R. Tính bán kính R theo a.
Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?
Cho tam giác ABC vuông tại A, \(BC = a\sqrt 3 \), M là trung điểm của BC và có \(\overrightarrow {AM} .\overrightarrow {BC} = \frac{{{a^2}}}{2}\). Tính cạnh AB, AC.
Trong khôn gian với hệ tọa độ Oxyz, cho các điểm A(2; 0; 0), B(0; 3; 0), C(0; 0; –4). Gọi H là trực tâm tam giác ABC. Tìm phương trình tham số của đường thẳng OH trong các phương án sau:
Biết rằng phương trình \({\left[ {{{\log }_{\frac{1}{3}}}\left( {9{\rm{x}}} \right)} \right]^2} + {\log _3}\frac{{{x^2}}}{{81}} - 7 = 0\) có hai nghiệm phân biệt x1; x2. Tính P = x1x2.
Cho hai số thực a và b với 1 < a < b. Khẳng định nào dưới đây là đúng?
Cho hình nón đỉnh S, góc ở đỉnh bằng 120°, đáy là hình tròn (O; 3R). Cắt hình nón bởi mặt phẳng qua S và tạo với đáy góc 60°. Diện tích thiết diện là:
