- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 54)
-
12476 lượt thi
-
48 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x2 – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Phương trình: 3f(x2 – 4x) = m (1)
Đặt u = x2 – 4x
Ta có bảng biến thiên sau
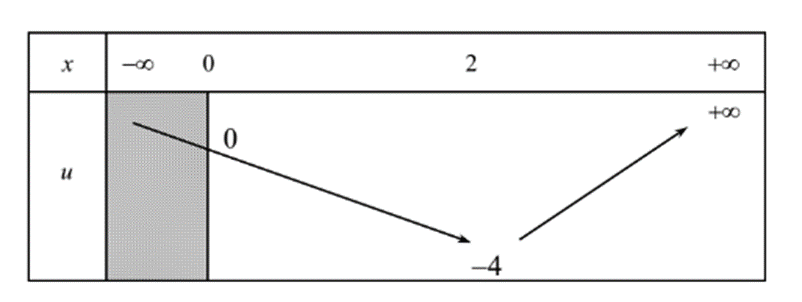
Ta thấy:
+) Với u < –4, phương trình (1) vô nghiệm
+) Với u = –4, phương trình (1) có một nghiệm x = 2 > 0
+) Với –4 < u < 0, phương trình (1) có hai nghiệm x > 0
+) Với u ≥ 0, phương trình (1) có một nghiệm x > 0
Khi đó 3f(x2 – 4x) = m
\( \Rightarrow f\left( u \right) = \frac{m}{3}\) (2)
Ta thấy:
+) Nếu \(\frac{m}{3} = - 3 \Leftrightarrow m = - 9\) thì phương trình (2) có một nghiệm u = 0
Nên phương trình (1) có một nghiệm x > 0
+) Nếu \( - 3 < \frac{m}{3} < - 2 \Leftrightarrow - 9 < m < - 6\) thì phương trình (2) có một nghiệm u > 0 và một nghiệm u ∈ (–2; 0)
Nên phương trình (1) có ba nghiệm x > 0
+) Nếu \(\frac{m}{3} = - 2 \Leftrightarrow m = - 6\) thì phương trình (2) có một nghiệm u = –4, một nghiệm u ∈ (–2; 0) và một nghiệm u > 0
Nên phương trình (1) có bốn nghiệm x > 0
+) Nếu \( - 2 < \frac{m}{3} < 2 \Leftrightarrow - 6 < m < 6\) thì phương trình (2) có một nghiệm u < –4, hai nghiệm u ∈ (–4; 0) và một nghiệm u > 0
Nên phương trình (1) có năm nghiệm x > 0
+) Nếu \(\frac{m}{3} = 2 \Leftrightarrow m = 6\) thì phương trình (2) có một nghiệm u < –4, một nghiệm u = –2 và một nghiệm u > 0
Nên phương trình (1) có ba nghiệm x > 0
+) Nếu \(\frac{m}{3} > 2 \Leftrightarrow m > 6\) thì phương trình (2) có một nghiệm u < –4 và một nghiệm u > 0
Nên phương trình (1) có một nghiệm x > 0
Suy ra –9 < m ≤ 6
Do đó m ∈ {–8; –7; –6; –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5; 6}
Vậy ta chọn đáp án A.
Câu 2:
Tìm m để \(y = \frac{{{x^2} + m{\rm{x}}}}{{1 - x}}\) có cực trị và khoảng cách giữa 2 điểm cực trị bằng 10.
 Xem đáp án
Xem đáp án
\(y' = \frac{{ - \left( {{x^2} - 2{\rm{x}} - m} \right)}}{{{{\left( {1 - x} \right)}^2}}}\)
Để hàm số \(y = \frac{{{x^2} + m{\rm{x}}}}{{1 - x}}\) có 2 cực trị
⇔ y’ = 0 có hai nghiệm phân biệt
⇔ x2 – 2x – m = 0 có hai nghiệm phân biệt
Điều kiện \(\left\{ \begin{array}{l}f\left( 1 \right) = - 1 - m \ne 0\\\Delta ' = 1 + m > 0\end{array} \right. \Leftrightarrow m > - 1\)
Theo định lý Vi – ét, hai nghiệm của phương trình thỏa mãn
\(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}.{x_2} = - m\end{array} \right.{\rm{ }}(1)\)
Khoảng cách giữa hai điểm cực trị là
\({d^2} = {\left( {{{\rm{x}}_1} - {x_2}} \right)^2} + {\left( {{y_1} - {y_2}} \right)^2} = {\left( {{{\rm{x}}_1} - {x_2}} \right)^2} + {\left( { - {x_1} + \frac{{m + 1}}{{1 - {x_1}}} + {x_2} - \frac{{m + 1}}{{1 - {x_2}}}} \right)^2} = 100\)
\( \Leftrightarrow {x_1}^2 - 2{{\rm{x}}_1}{x_2} + {x_2}^2 + {\left( {{x_2} - {x_1} + \frac{{\left( {m + 1} \right)\left( {1 - {x_2}} \right) - \left( {m + 1} \right)\left( {1 - {x_1}} \right)}}{{\left( {1 - {x_1}} \right)\left( {1 - {x_2}} \right)}}} \right)^2} = 100\)
\( \Leftrightarrow \left( {{x_1}^2 + 2{{\rm{x}}_1}{x_2} + {x_2}^2} \right) - 4{{\rm{x}}_1}{x_2} + {\left( {{x_2} - {x_1} + \frac{{m - m{{\rm{x}}_2} + 1 - {x_2} - m + m{{\rm{x}}_1} - 1 + {x_1}}}{{\left( {1 - {x_1}} \right)\left( {1 - {x_2}} \right)}}} \right)^2} = 100\)
\( \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{{\rm{x}}_1}{x_2} + {\left( {{x_2} - {x_1} + \frac{{ - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{1 - {x_1} - {x_2} + {x_1}{x_2}}}} \right)^2} = 100\)
\( \Leftrightarrow {2^2} - 4.\left( { - m} \right) + {\left( {{x_2} - {x_1} + \frac{{ - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{1 - 2 - m}}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + {\left( {{x_2} - {x_1} + \frac{{ - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{ - 1 - m}}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + {\left( {\frac{{\left( {{x_2} - {x_1}} \right)\left( { - 1 - m} \right) - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{ - 1 - m}}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + {\left( {\frac{{ - {x_2} - m{{\rm{x}}_2} + {x_1} + m{{\rm{x}}_1} - m{{\rm{x}}_2} - {x_2} + m{{\rm{x}}_1} + {x_1}}}{{ - 1 - m}}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + {\left( {\frac{{2{x_2} + 2m{{\rm{x}}_2} - 2{x_1} - 2m{{\rm{x}}_1}}}{{1 + m}}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + 4{\left( {\frac{{\left( {{x_2} - {x_1}} \right)\left( {1 + m} \right)}}{{1 + m}}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + 4{\left( {{x_2} - {x_1}} \right)^2} = 100\)
\( \Leftrightarrow 4 + 4m + 4\left[ {{{\left( {{x_2} + {x_1}} \right)}^2} - 2{{\rm{x}}_1}{x_2}} \right] = 100\)
\( \Leftrightarrow 4 + 4m + 4\left( {4 + 4m} \right) = 100\)
\( \Leftrightarrow 20m + 20 = 100\)
\( \Leftrightarrow 20m = 80\)
\( \Leftrightarrow m = 4\)
Vậy m = 4.
Câu 3:
Phân tích đa thức thành nhân tử (x + y)3 – ( x – y)3.
 Xem đáp án
Xem đáp án
Ta có:
\(\begin{array}{l}{(x + y)^3} - {(x - y)^3}\\ = {x^3} + 3{x^2}y + 3x{y^2} + {y^3} - {x^3} + 3{x^2}y - 3x{y^2} + {y^3}\\ = 6{x^2}y + 2{y^3}\\ = 2y\left( {3{x^2} + {y^2}} \right).\end{array}\)
Câu 4:
 Xem đáp án
Xem đáp án
Ta có:
x2 + 6x + 9
= x2 + 2 . 3 . x + 32
= (x + 3)2.
Câu 5:
Cho \(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\)
a) Tìm điều kiện xác định rồi rút gọn A
b) Tìm a để \[{\rm{A}} < \frac{1}{3}\].
 Xem đáp án
Xem đáp án
a) Điều kiện xác định a ≥ 0, a ≠ 1
\(A = \frac{1}{{2 + 2\sqrt a }} + \frac{1}{{2 - 2\sqrt a }} - \frac{{{a^2} + 1}}{{1 - {a^2}}}\)
\({\rm{A}} = \frac{1}{{2\left( {1 + \sqrt a } \right)}} + \frac{1}{{2\left( {1 - \sqrt a } \right)}} - \frac{{{a^2} + 1}}{{\left( {1 - a} \right)\left( {1 + a} \right)}}\)
\({\rm{A}} = \frac{1}{{2\left( {1 + \sqrt a } \right)}} + \frac{1}{{2\left( {1 - \sqrt a } \right)}} - \frac{{{a^2} + 1}}{{\left( {1 - \sqrt a } \right)\left( {1 + \sqrt a } \right)\left( {1 + a} \right)}}\)
\(A = \frac{{\left( {1 - \sqrt a } \right)\left( {1 + a} \right) + \left( {1 + \sqrt a } \right)\left( {1 + a} \right) - \left( {{a^2} + 1} \right)2}}{{2\left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right)\left( {1 + a} \right)}}\)
\(A = \frac{{1 + a - \sqrt a - a\sqrt a + 1 + a + \sqrt a + a\sqrt a - 2{a^2} + 2}}{{2\left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right)\left( {1 + a} \right)}}\)
\({\rm{A}} = \frac{{2a - 2{a^2}}}{{2\left( {1 - a} \right)\left( {1 + a} \right)}}\)
\({\rm{A}} = \frac{{2a\left( {1 - a} \right)}}{{2\left( {1 - a} \right)\left( {1 + a} \right)}}\)
\({\rm{A}} = \frac{a}{{1 + a}}\)
b) Để \[{\rm{A}} < \frac{1}{3}\]\( \Leftrightarrow \frac{a}{{1 + a}} < \frac{1}{3}\)
\( \Leftrightarrow \frac{a}{{1 + a}} - \frac{1}{3} < 0\)\( \Leftrightarrow \frac{{3a - a - 1}}{{1 + a}} < 0\)
\( \Leftrightarrow 2{\rm{a}} - 1 < 0\)\( \Leftrightarrow {\rm{a}} < \frac{1}{2}\)
Mà a ≥ 0, a ≠ 1
Suy ra \({\rm{0}} \le {\rm{a}} < \frac{1}{2}\)
Vậy \({\rm{0}} \le {\rm{a}} < \frac{1}{2}\).
Câu 6:
Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua (C): x2 + y2 – 2x + 4y – 1 = 0 với \(\overrightarrow v = \left( {1;2} \right)\) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo tính chất của phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
Ta có đường tròn (C) có tâm I(1; −2), bán kính \(R = \sqrt 6 \)
Với phép tịnh tiến theo \(\overrightarrow v = \left( {1;2} \right)\) thì ta có \(\left\{ \begin{array}{l}x' = x + 1\\y' = y + 2\end{array} \right.\)
Suy ra \[{T_{\overrightarrow v }}\left( I \right) = I'\left( {2;0} \right)\]
Vậy đường tròn (C') có tâm I'(2;0), bán kính \(R' = R = \sqrt 6 \) có phương trình \({\left( {x - 2} \right)^2} + {y^2} = 6\), ta chọn đáp án B.
Câu 7:
Tìm giá trị nhỏ nhất của hàm số \(y = 3{\rm{x}} + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).
 Xem đáp án
Xem đáp án
Ta có :
\(y' = 3 - \frac{8}{{{x^3}}}\)
\(\begin{array}{l}y' = 0 \Leftrightarrow 3 - \frac{8}{{{x^3}}} = 0\\ \Leftrightarrow x = \frac{2}{{\sqrt[3]{3}}} \Rightarrow y = \frac{9}{{\sqrt[3]{3}}} = 3\sqrt[3]{9}.\end{array}\)
Vậy giá trị nhot nhất của \(y = 3{\rm{x}} + \frac{4}{{{x^2}}}\) là \(3\sqrt[3]{9}\).
Câu 8:
Cho hàm số \((C):y = \frac{{x + 2}}{{x - 1}}\)
Cho điểm M(0; m). Xác định m để từ A kẻ được 2 tiếp tuyến đến (C) sao cho 2 tiếp tuyến tương ứng nằm về hai phía đối với trục Ox.
 Xem đáp án
Xem đáp án
Đường thẳng d đi qua điểm M, hệ số góc k có phương trình y = kx + m
d là tiếp tuyến \( \Leftrightarrow \left\{ \begin{array}{l}\frac{{x + 2}}{{x - 1}} = k{\rm{x}} + m\\\frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} = k\end{array} \right.\) có nghiệm
Thay \(k = \frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}}\) vào phương trình y = kx + m ta được:
\(\frac{{x + 2}}{{x - 1}} = \frac{{ - 3{\rm{x}}}}{{{{\left( {x - 1} \right)}^2}}} + m\)
\( \Leftrightarrow \frac{{\left( {x + 2} \right)\left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{ - 3{\rm{x}}}}{{{{\left( {x - 1} \right)}^2}}} + \frac{{m{{\left( {x - 1} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}}\)
⇔ x2 + x – 2 = –3x + m(x2 – 2x + 1)
⇔ x2 + x – 2 = –3x + mx2 – 2mx + m
⇔ (m – 1)x2 – 2(m + 2)x + m + 2 = 0 (*)
Để từ M kẻ được hai tiếp tuyến thì phương trình (*) có hai nghiệm phân biệt khác 1
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = 3\left( {m + 2} \right) > 0\\m \ne 1\\m - 1 - 2\left( {m + 2} \right) + m + 2 \ne 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > - 2\\m \ne 1\end{array} \right.\)
Khi đó tọa độ hai điểm là M1(x1; y1) và M2(x2; y2) với x1; x2 là nghiệm của phương trùnh (*) và \({y_1} = \frac{{{x_1} + 2}}{{{x_1} - 1}};{y_2} = \frac{{{x_2} + 2}}{{{x_2} - 1}}\)
Để M1; M2 nằm về hai phía của Ox thì y1 . y2 = 0
\( \Leftrightarrow \frac{{{x_1} + 2}}{{{x_1} - 1}}.\frac{{{x_2} + 2}}{{{x_2} - 1}} < 0\)
\( \Leftrightarrow \frac{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}}{{\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right)}} < 0\)
\( \Leftrightarrow \frac{{{x_1}{x_2} + 2{x_1} + 2{{\rm{x}}_2} + 4}}{{{x_1}{x_2} - {x_1} - {x_2} + 1}} < 0\)
Áp dụng định lý Vi – ét ta có
\[{{\rm{x}}_1} + {x_2} = \frac{{2\left( {m + 2} \right)}}{{m - 1}};{x_1}{x_2} = \frac{{m + 2}}{{m - 1}}\]
Suy ra \(\frac{{\frac{{m + 2}}{{m - 1}} + \frac{{4\left( {m + 2} \right)}}{{m - 1}} + 4}}{{\frac{{m + 2}}{{m - 1}} - \frac{{2\left( {m + 2} \right)}}{{m - 1}} + 1}} < 0\)
\( \Leftrightarrow \frac{{\left( {m + 2} \right) + 4\left( {m + 2} \right) + 4\left( {m - 1} \right)}}{{\left( {m + 2} \right) - 2\left( {m + 2} \right) + \left( {m - 1} \right)}} < 0\)
\( \Leftrightarrow \frac{{9m + 6}}{{ - 3}} < 0\)\( \Leftrightarrow 9m + 6 > 0\)\( \Leftrightarrow m > \frac{{ - 2}}{3}\)
Mà \(\left\{ \begin{array}{l}m > - 2\\m \ne 1\end{array} \right.\)
Suy ra \(m > \frac{{ - 2}}{3};m \ne 1\)
Vậy \(m > \frac{{ - 2}}{3};m \ne 1\).
Câu 9:
Tìm các số nguyên x, y thỏa mãn x3 + 2x2 + 3x + 2 = y3.
 Xem đáp án
Xem đáp án
Ta có:
\(\begin{array}{l}2{x^2} + 3x + 2 = 2\left( {{x^2} + \frac{3}{2}x + 1} \right) = 2\left( {{x^2} + 2 \cdot x \cdot \frac{3}{4} + \frac{9}{{16}} + \frac{7}{{16}}} \right)\\ = 2\left[ {{{\left( {x + \frac{3}{4}} \right)}^2} + \frac{7}{{16}}} \right] = 2{\left( {x + \frac{3}{4}} \right)^2} + \frac{7}{8}\end{array}\)
Vì \(2{\left( {x + \frac{3}{4}} \right)^2} \ge 0;\forall x\)
Nên \(2{\left( {x + \frac{3}{4}} \right)^2} + \frac{7}{8} > 0;\forall x\)
Mà x3 + 2x2 + 3x + 2 = y3
Suy ra x3 < y3
Giả sử y3 < (x + 2)3
⇔ x3 + 2x2 + 3x + 2 < x3 + 6x2 + 12x + 8
⇔ – 4x2 – 9x – 6 < 0
⇔ 4x2 + 9x + 6 > 0
\(\begin{array}{l} \Leftrightarrow 4{x^2} + 9x + 6 > 0\\ \Leftrightarrow 4\left( {{x^2} + \frac{9}{4}x + \frac{{81}}{{64}}} \right) + \frac{{15}}{{16}} > 0\\ \Leftrightarrow 4\left( {{x^2} + 2 \cdot x \cdot \frac{9}{8} + \frac{{81}}{{64}}} \right) + \frac{{15}}{{16}} > 0\\ \Leftrightarrow 4{\left( {x + \frac{9}{8}} \right)^2} + \frac{{15}}{{16}} > 0{\rm{ }}\end{array}\) (luôn đúng)
Do đó y3 < (x + 2)3
Mà x3 < y3
Nên x3 < y3 < (x + 2)3
Lại có y3 là lập phương của một số nguyên, giữa x3 và (x + 2)3 chỉ có 1 số lập phương duy nhất là (x + 1)3
Do đó y 3 = (x + 1)3
⇔ x3 + 2x2 + 3x + 2 = x3 + 3x2 + 3x + 1
⇔ x2 – 1 = 0
⇔ (x – 1)(x + 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{y^3} = 1 + 2 + 3 + 2 = 8\\{y^3} = - 1 + 2 - 3 + 2 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}y = 2\\y = 0\end{array} \right.\)
Vậy (x; y) = (1; 2) hoặc (x; y) = (–1; 0).
Câu 10:
Tập xác định của hàm số y = logx là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hàm số y = logx xác định
⇔ x > 0
Suy ra tập xác định của hàm số y = logx là (0; +∞)
Vậy ta chọn đáp án B.
Câu 11:
Cho các số dương x, y, z thỏa mãn điều kiện xy + yz + zx = xyz. Chứng minh rằng:
\(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \).
 Xem đáp án
Xem đáp án
Đặt \(a = \frac{1}{x};b = \frac{1}{y};c = \frac{1}{z}\)
Suy ra a, b, c > 0 và \(a + b + c = \frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{{yz + x{\rm{z}} + xy}}{{xyz}} = 1\)
Khi đó \(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \)
\( \Leftrightarrow \sqrt {\frac{1}{a} + \frac{1}{{bc}}} + \sqrt {\frac{1}{b} + \frac{1}{{ac}}} + \sqrt {\frac{1}{c} + \frac{1}{{ab}}} \ge \sqrt {\frac{1}{{abc}}} + \sqrt {\frac{1}{a}} + \sqrt {\frac{1}{b}} + \sqrt {\frac{1}{c}} \)
\( \Leftrightarrow \sqrt {a + bc} + \sqrt {b + ac} + \sqrt {c + ab} \ge \sqrt {ab} + \sqrt {bc} + \sqrt {ac} + 1\)
Ta có:
\(\begin{array}{l}\sqrt {a + bc} = \sqrt {a(a + b + c) + bc} = \sqrt {{a^2} + a(b + c) + bc} \ge \sqrt {{a^2} + 2a\sqrt {bc} + bc} \\ \Rightarrow \sqrt {a + bc} \ge \sqrt {{{(a + \sqrt {bc} )}^2}} = a + \sqrt {bc} \end{array}\)
Chứng minh tương tự:
\(\begin{array}{l}\sqrt {b + ac} \ge b + \sqrt {ac} ;\\\sqrt {c + ab} \ge c + \sqrt {ab} \end{array}\)
Cộng theo vế các bất đẳng thức trên ta được
\(\sqrt {a + bc} + \sqrt {b + ac} + \sqrt {c + ab} \ge \sqrt {ab} + \sqrt {bc} + \sqrt {ac} + a + b + c\)
\( \Leftrightarrow \sqrt {a + bc} + \sqrt {b + ac} + \sqrt {c + ab} \ge \sqrt {ab} + \sqrt {bc} + \sqrt {ac} + 1\)
Suy ra \(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \)
Dấu “ = ” xảy ra khi \(a = b = c = \frac{1}{3} \Leftrightarrow x = y = z = 3\)
Vậy \(\sqrt {x + yz} + \sqrt {y + x{\rm{z}}} + \sqrt {z + xy} \ge \sqrt {xyz} + \sqrt x + \sqrt y + \sqrt z \).
Câu 12:
 Xem đáp án
Xem đáp án
Ta có: \(\left\{ \begin{array}{l}y + x{y^2} = 6{{\rm{x}}^2}\\1 + {x^2}{y^2} = 5{{\rm{x}}^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\frac{y}{{{x^2}}} + \frac{{{y^2}}}{x} = 6\\\frac{1}{{{x^2}}} + {y^2} = 5\end{array} \right.\)
Đặt \[{\rm{a}} = \frac{1}{x}\] ta có: \(\left\{ \begin{array}{l}{a^2}y + a{y^2} = 6\\{a^2} + {y^2} = 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}ay\left( {a + y} \right) = 6\\{\left( {a + y} \right)^2} - 2{\rm{a}}y = 5\end{array} \right.\)
Đặt ay = z, a + y = t
Ta có \(\left\{ \begin{array}{l}t{\rm{z}} = 6\\{t^2} - 2{\rm{z}} = 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\rm{z}} = \frac{{{t^2} - 5}}{2}\\t.\frac{{{t^2} - 5}}{2} = 6\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\rm{z}} = \frac{{{t^2} - 5}}{2}\\{t^3} - 5t - 12 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\rm{z}} = \frac{{{t^2} - 5}}{2}\\\left( {t - 3} \right)\left( {{t^2} + 3t + 4} \right) = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\rm{z}} = \frac{{{t^2} - 5}}{2}\\t - 3 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\rm{z}} = 2\\t = 3\end{array} \right.\)
Suy ra \(\left\{ \begin{array}{l}ay = 2\\a + y = 3\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y\left( {3 - y} \right) = 2\\a = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y^2} - 3y + 2 = 0\\a = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y = 1\\y = 2\end{array} \right.\\a = 3 - y\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}y = 1\\a = 2\end{array} \right.\\\left\{ \begin{array}{l}y = 2\\a = 1\end{array} \right.\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}y = 1\\\frac{1}{x} = 2\end{array} \right.\\\left\{ \begin{array}{l}y = 2\\\frac{1}{x} = 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}y = 1\\x = \frac{1}{2}\end{array} \right.\\\left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\end{array} \right.\)
Vậy hệ phương trình có nghiệm (x; y) = (1; 2) hoặc \(\left( {x;y} \right) = \left( {\frac{1}{2};1} \right)\).
Câu 13:
Đạo hàm của hàm số y = log(1 – x) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(\left[ {\log \left( {1 - x} \right)} \right]' = \frac{{ - 1}}{{\left( {1 - x} \right)\ln 10}} = \frac{1}{{\left( {x - 1} \right)\ln 10}}\)
Vậy ta chọn đáp án A.
Câu 14:
Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì không thể nhân hai mũ khác cơ số, khác cả số mũ nên đáp án A sai
Ta chỉ có thể nhân 2 mũ có cùng cơ số
xm . xn = xm+n
Vậy ta chọn đáp án A.
Câu 15:
Hình bình hành ABCD có AC ⊥ AD và AD = 3,5; \(\widehat D = 50^\circ \). Tính diện tích ABCD.
 Xem đáp án
Xem đáp án

Vì AC ⊥ AD nên tam giác ACD vuông tại A
Suy ra \(\tan \widehat {A{\rm{D}}C} = \frac{{AC}}{{A{\rm{D}}}}\)
Do đó AC = AD . tan50° = 3,5 . tan50°
Ta có \[{{\rm{S}}_{AC{\rm{D}}}} = \frac{1}{2}AC.A{\rm{D}} = \frac{1}{2}.3,5.\tan 50^\circ .3,5 = \frac{{49}}{8}.\tan 50^\circ \]
Diện tích hình hình hành ABCD là
\({S_{ABC{\rm{D}}}} = 2{{\rm{S}}_{AC{\rm{D}}}} = 2.\frac{{49}}{8}.\tan 50^\circ \approx 14,6.\)
Câu 16:
Tìm tất cả các giá trị của tham số m để hàm số y = x3 + x2 + mx + 1 đồng biến trên khoảng (–∞; +∞)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
y’ = 3x2 + 2x + m
Xét phương trình y’ = 0
⇔ 3x2 + 2x + m = 0
Hàm số đồng biến trên R ⇔ y’ ≥ 0, ∀x
⇔ ∆’ ≤ 0 ⇔ 12 – 3m ≤ 0 \( \Leftrightarrow m \ge \frac{1}{3}\)
Vậy ta chọn đáp án C.
Câu 17:
Chứng minh bất đẳng thức sinx < x với mọi x > 0 và sinx > x với mọi x < 0.
 Xem đáp án
Xem đáp án
Xét hàm số f(x) = x – sinx liên tục trên nửa khoảng \(\left[ {0;\left. {\frac{\pi }{2}} \right)} \right.\)
Đạo hàm f’ = 1 – cosx > 0 với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\)
Do đó hàm số đồng biến trên \(\left[ {0;\left. {\frac{\pi }{2}} \right)} \right.\)
Từ đó với mọi \(x \in \left( {0;\frac{\pi }{2}} \right)\) ta có:
f(x) > f(0) = 0
Suy ra x – sinx > 0; \(\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
⇔ x > sinx; \(\forall x \in \left( {0;\frac{\pi }{2}} \right)\)
Với \(x \ge \frac{\pi }{2}\) thì x > 1 ≥ sinx
Vậy sinx < x với mọi x > 0
Xét hàm số f(x) = x – sinx liên tục trên nửa khoảng \(\left( {\frac{{ - \pi }}{2};\left. 0 \right]} \right.\)
Đạo hàm f’ = 1 – cosx > 0 với mọi \(x \in \left( { - \frac{\pi }{2};0} \right)\)
Do đó hàm số đồng biến trên \(\left( {\frac{{ - \pi }}{2};\left. 0 \right]} \right.\)
Từ đó với mọi \(x \in \left( { - \frac{\pi }{2};0} \right)\) ta có:
f(x) < f(0) = 0
Suy ra x – sinx < 0; \(\forall x \in \left( { - \frac{\pi }{2};0} \right)\)
⇔ x < sinx; \(\forall x \in \left( { - \frac{\pi }{2};0} \right)\)
Với \(x \le \frac{\pi }{2}\) thì \(x \le \frac{{ - \pi }}{2} < - 1 \le {\mathop{\rm s}\nolimits} {\rm{inx}}\)
Vậy sinx > x với mọi x < 0.
Câu 18:
Cho hàm số y = – x3 + 3x2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có y’ = – 3x2 + 6x + 3m ≤ 0, ∀x > 0
⇔ 3m ≤ 3x2 – 6x, ∀x > 0
⇔ 3m ≤ 3(x2 – 2x + 1) – 3, ∀x > 0
⇔ 3m ≤ 3(x – 1)2 – 3, ∀x > 0
Vì 3(x – 1)2 ≥ 0 với mọi x
Nên 3(x – 1)2 – 3 ≥ –3 với mọi x
Suy ra 3x2 – 6x nhỏ nhất bằng –3 khi x = 1
Do đó 3m ≤ –3 ⇔ m ≤ –1
Vậy ta chọn đáp án C.
Câu 19:
Tính tổng: S = 12 + 22 + 32 + ... + n2.
 Xem đáp án
Xem đáp án
Ta có:
n2 – n = n(n – 1)
⇔ n2 = (n – 1)n + n
Khi đó:
S = 12 + 22 + 32 + ... + n2
S = 1 + 1 . 2 + 2 . 3 + ... + (n – 1)n + n
S = [1 . 2 + 2 . 3 + ... + (n – 1)n] + (1 + 2 + ... + n)
\[{\rm{S}} = \frac{{\left( {n - 1} \right)n\left( {n + 1} \right)}}{3} + \frac{{n\left( {n + 1} \right)}}{2}\]
\[{\rm{S}} = \frac{{2\left( {n - 1} \right)n\left( {n + 1} \right) + 3n\left( {n + 1} \right)}}{6}\]
\[{\rm{S}} = \frac{{n\left( {n + 1} \right)\left( {2n - 2 + 3} \right)}}{6}\]
\[{\rm{S}} = \frac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\].
Câu 20:
Cho tam giác ABC có cạnh a, b, c thỏa mãn bc = a2.
Chứng minh rằng sinB.sinC = sin2A và hb . hc = ha2.
 Xem đáp án
Xem đáp án
• Ta có: \(\frac{{\sin {\rm{A}}}}{a} = \frac{{\sin B}}{b} = \frac{{\sin C}}{c} = 2{\rm{R}}\)
Suy ra \(a = \frac{{\sin B}}{{2{\rm{R}}}};\,\,b = \frac{{\sin {\rm{A}}}}{{2{\rm{R}}}};\,\,c = \frac{{\sin C}}{{2{\rm{R}}}}\)
Mà bc = a2
Suy ra \(\frac{{\sin B}}{{2{\rm{R}}}}.\frac{{\sin C}}{{2{\rm{R}}}} = {\left( {\frac{{\sin {\rm{A}}}}{{2{\rm{R}}}}} \right)^2}\)\( \Leftrightarrow \frac{{\sin B.\sin C}}{{4{{\rm{R}}^2}}} = \frac{{{{\sin }^2}A}}{{4{{\rm{R}}^2}}}\)
Do đó sin B . sin C = sin2A
• Ta có: \[S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}\]
Suy ra \[a = \frac{{2{\rm{S}}}}{{{h_a}}};b = \frac{{2{\rm{S}}}}{{{h_b}}};c = \frac{{2{\rm{S}}}}{{{h_c}}}\]
Mà bc = a2
Suy ra \[{\left( {\frac{{2{\rm{S}}}}{{{h_a}}}} \right)^2} = \frac{{2{\rm{S}}}}{{{h_b}}}.\frac{{2{\rm{S}}}}{{{h_c}}}\]
\[ \Leftrightarrow \frac{{4{{\rm{S}}^2}}}{{{h_a}^2}} = \frac{{{\rm{4}}{{\rm{S}}^2}}}{{{h_b}.{h_c}}}\]
Do đó hb . hc = ha2.
Câu 21:
Cho 4 chữ số 1, 5, 8, 9 có thể viết được mấy số có 4 chữ số khác nhau từ các chữ số trên.
 Xem đáp án
Xem đáp án
Có 4 cách chọn chữ số hàng nghìn
Có 3 cách chọn chữ số hàng trăm
Có 2 cách chọn chữ số hàng chục
Có 1 cách chọn chữ số hàng đơn vị
Suy ra lập được số các số có 4 chữ số khác nhau từ các chữ số 1, 5, 8, 9, là:
4 × 3 × 2 × 1 = 24 (số)
Vậy lập được 24 số thỏa mãn yêu cầu đề bài.
Câu 22:
Tìm x biết x² – 9 + 5(x – 3) = 0.
 Xem đáp án
Xem đáp án
Ta có:
x² – 9 + 5(x – 3) = 0
⇔ x² – 9 + 5x – 15 = 0
⇔ x² + 5x – 24 = 0
⇔ x² – 3x + 8x – 24 = 0
⇔ x(x – 3) + 8(x – 3) = 0
⇔ (x – 3)(x + 8) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 8 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 8\end{array} \right.\)
Vậy x = 3 hoặc x = –8.
Câu 23:
 Xem đáp án
Xem đáp án
Ta có:
(102 + 112 + 122) : (132 + 142)
= (100 + 121 + 144) : (169 + 196)
= 365 : 365 = 1.
Câu 24:
Tìm x biết (8x – 7)(8x – 5)(2x – 1)(4x – 1) = 9.
 Xem đáp án
Xem đáp án
Ta có:
(8x – 7)(8x – 5)(2x – 1)(4x – 1) = 9
⇔ (8x – 7)(8x – 5)(8x – 4)(8x – 2) = 72
Đặt 8x – 5 = a
Khi đó ta có:
(a – 2)a(a + 1)(a + 3) = 72
⇔ (a2 – 2a)(a2 + 4a + 3) – 72 = 0
⇔ a4 – 4a3 + 3a2 – 2a3 – 8a2 – 6a – 72 = 0
⇔ a4 + 4a3 – 2a3 – 8a2 + 3a2 + 12a – 18a – 72 = 0
⇔ a3(a + 4) – 2a2(a + 4) + 3a(a + 4) – 18(a + 4) = 0
⇔ (a + 4)(a3 – 2a2 + 3a – 18) = 0
⇔ (a + 4)(a3 – 3a2 + a2 – 3a + 6a – 18) = 0
⇔ (a + 4)[a2(a – 3) + a(a – 3) + 6(a – 3)] = 0
⇔ (a + 4)(a – 3)(a2 + a + 6) = 0 (*)
Vì \[{{\rm{a}}^2} + a + 6 = {a^2} + 2.a.\frac{1}{2} + \frac{1}{4} + \frac{{23}}{4} = {\left( {a + \frac{1}{2}} \right)^2} + \frac{{23}}{4} > 0\]
Nên \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}a + 4 = 0\\a - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = - 4\\a = 3\end{array} \right.\)
Suy ra \(\left[ \begin{array}{l}8{\rm{x}} - 5 = - 4\\8{\rm{x}} - 5 = 3\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}8{\rm{x}} = 1\\8{\rm{x}} = 8\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{8}\\x = 1\end{array} \right.\)
Vậy x = 1 hoặc \[{\rm{x}} = \frac{1}{8}\].
Câu 25:
Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
+) Với mọi số tự nhiên thì có các trường hợp sau:
n = 3k ⇒ n2 + 1 = (3k)2 + 1 chia 3 dư 1
n = 3k + 1 ⇒ n2 + 1 = (3k + 1)2 + 1 = 9k2 + 6k + 2 chia 3 dư 2
n = 3k + 2 ⇒ n2 + 1 = (3k + 2)2 + 1 = 9k2 + 12k + 5 chia 3 dư 2
Suy ra ∀ n ∈ ℕ, n2 + 1 không chia hết cho 3, mệnh đề A đúng
+) Với mọi số tự nhiên thì có các trường hợp sau:
n = 4k ⇒ n2 + 1 = (4k)2 + 1 chia 4 dư 1
n = 4k + 1 ⇒ n2 + 1 = (4k + 1)2 + 1 = 16k2 + 8k + 2 chia 4 dư 2
n = 4k + 2 ⇒ n2 + 1 = (4k + 2)2 + 1 = 16k2 + 16k + 5 chia 4 dư 1
n = 4k + 3 ⇒ n2 + 1 = (4k + 3)2 + 1 = 16k2 + 24k + 10 chia 4 dư 2
Suy ra ∀ n ∈ ℕ, n2 + 1 không chia hết cho 4, do đó mệnh đề D sai.
+) Ta có: x = – 4 < 3, nhưng |x| = | – 4| = 4 > 3, suy ra mệnh đề B sai
+) Với x = 1, ta có (x – 1)2 = (1 – 1)2 = 0 và x – 1 = 1 – 1 = 0, do đó mệnh đề C sai
Vậy ta chọn đáp án A.
Câu 26:
Tính \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\).
 Xem đáp án
Xem đáp án
Ta có:
\(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}}\)
\( = \frac{{{{\left( {{x^3}} \right)}^2} - {{\left( {{y^3}} \right)}^2}}}{{{x^3}(x - y) + {y^3}(x - y)}}\)
\( = \frac{{\left( {{x^3} + {y^3}} \right)\left( {{x^3} - {y^3}} \right)}}{{\left( {{x^3} + {y^3}} \right)(x - y)}}\)\( = \frac{{{x^3} - {y^3}}}{{x - y}}\)
\( = \frac{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}}{{x - y}}\)\( = {x^2} + xy + {y^2}\)
Vậy \(\frac{{{x^6} - {y^6}}}{{{x^4} - {y^4} - {x^3}y + x{y^3}}} = {x^2} + xy + {y^2}\).
Câu 27:
Cho a là số thực dương, a ≠ 1 và \(P = {\log _{\sqrt[3]{a}}}{a^3}\). Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
\(P = {\log _{\sqrt[3]{a}}}{a^3} = {\log _{{a^{\frac{1}{3}}}}}{a^3} = 3.3{\log _a}a = 9\,\,\left( {a > 0,a \ne 1} \right)\)
Vậy ta chọn đáp án C.
Câu 28:
Cho Ax, By là các tiếp tuyến của \(\left( {O;\frac{{AB}}{2}} \right)\). Tiếp tuyến tại M của (O) cắt Ax, By, AB lần lượt tại C, D, E. AD và BC cắt nhau tại N
a) Tính AC. BD theo AB
b) Chứng minh MN vuông góc AB
c) So sánh 2 tỉ số \(\frac{{CM}}{{CE}};\frac{{DM}}{{DE}}\).
d) Chứng minh rằng đường thẳng EN đi qua trung điểm của các đoạn thẳng AC, BD. Xem đáp án
Xem đáp án
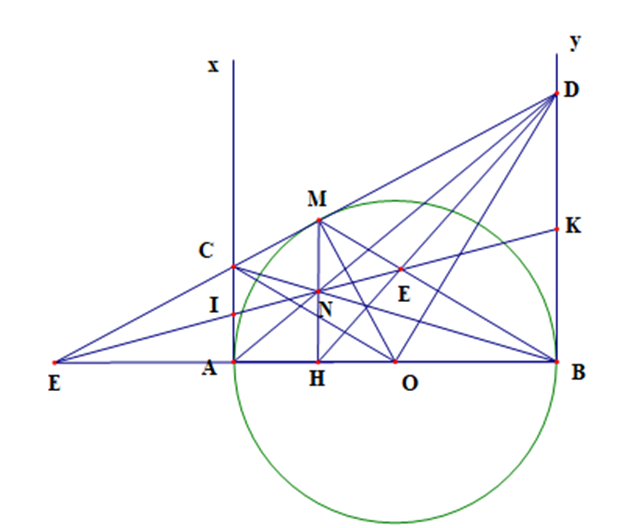
a) Xét (O) có CA, CM là hai tiếp tuyến cắt nhau tại C
Suy ra CA = CM, OC là tia phân giác của \(\widehat {AOM}\)
Do đó \(\widehat {COM} = \frac{1}{2}\widehat {AOM}\)
Xét (O) có DB, DM là hai tiếp tuyến cắt nhau tại D
Suy ra DB = DM, OD là tia phân giác của \(\widehat {BOM}\)
Do đó \(\widehat {DOM} = \frac{1}{2}\widehat {BOM}\)
Ta có: \(\widehat {COD} = \widehat {COM} + \widehat {DOM} = \frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.180^\circ = 90^\circ \)
Do đó tam giác COD vuông tại O
Mà OM ⊥ CD
Suy ra OM2 = CM . DM (hệ thức lượng trong tam giác vuông)
Mà CA = CM, DB = DM, \(OM = \frac{1}{2}AB\)
Suy ra \(CA.DB = \frac{{A{B^2}}}{4}\)
b) Vì AC // BD nên \(\frac{{AC}}{{B{\rm{D}}}} = \frac{{AN}}{{N{\rm{D}}}} = \frac{{CN}}{{NB}}\)
Mà CA = CM, DB = DM (chứng minh câu a)
Suy ra \(\frac{{CM}}{{DM}} = \frac{{AN}}{{N{\rm{D}}}}\)
Xét tam giác ACD có \(\frac{{CM}}{{DM}} = \frac{{AN}}{{N{\rm{D}}}}\)
Suy ra MN // CA
Mà AC ⊥ AB
Do đó MN ⊥ AB
c) Xét tam giác ACE vuông tại A có
\[\sin \widehat E = \frac{{CA}}{{CE}}\]
Mà CA = CM
Suy ra \[\sin \widehat E = \frac{{CM}}{{CE}}\] (1)
Xét tam giác EBD vuông tại B có
\[\sin \widehat E = \frac{{B{\rm{D}}}}{{DE}}\]
Mà BD = DM
Suy ra \[\sin \widehat E = \frac{{DM}}{{DE}}\] (2)
Từ (1) và (2) suy ra \(\frac{{CM}}{{CE}} = \frac{{DM}}{{DE}}\)
d) Gọi giao điểm của MN với AB là H
Giao điểm của AN với AC và BD lần lượt là I và K
Xét (O) đường kính AB có MN ⊥ AO
Mà MN cắt AO tại H
Suy ra H là trung điểm của AO
Xét tam giác DBE có MH // BD
Suy ra \(\frac{{MN}}{{DK}} = \frac{{NH}}{{BK}}\)
Do đó \(\frac{{MN}}{{NH}} = \frac{{DK}}{{BK}}\) (3)
Gọi giao điểm của MB và HD là E
Xét tam giác DKE có MN // KD
Suy ra \(\frac{{NH}}{{DK}} = \frac{{NE}}{{EK}}\)
Xét tam giác BKE có MN // BK
Suy ra \(\frac{{NM}}{{BK}} = \frac{{NE}}{{EK}}\)
Mà \(\frac{{NH}}{{DK}} = \frac{{NE}}{{EK}}\)
Do đó \(\frac{{NH}}{{DK}} = \frac{{MN}}{{BK}}\)
Hay \(\frac{{NM}}{{MH}} = \frac{{BK}}{{DK}}\) (4)
Từ (3) và (4) suy ra \(\frac{{DK}}{{BK}} = \frac{{BK}}{{DK}}\)
Do đó DK = BK, MN = NH
Hay EN đi qua trung điểm K của đoạn thẳng BD
Xét tam giác EHM có CA // MH
Suy ra \(\frac{{CI}}{{MN}} = \frac{{AI}}{{NH}}\)
Mà MN = NH
Suy ra CI = AI
Hay EN đi qua trung điểm I của đoạn thẳng AC
Vậy EN đi qua trung điểm của các đoạn thẳng AC, BD.
Câu 29:
Phân tích đa thức thành nhân tử: (x – 1)(x – 2)(x + 7)(x + 8) + 8.
 Xem đáp án
Xem đáp án
Ta có:
(x – 1)(x – 2)(x + 7)(x + 8) + 8
= (x – 1)(x + 7)(x – 2)(x + 8) + 8
= (x2 + 6x – 7)(x2 + 6x – 16) + 8
Đặt x2 + 6x – 7 = t, ta được
t(t – 9) + 8 = t2 – 9t + 8 = t2 – 8t – t + 8 = t(t – 8) – (t – 8) = (t – 8)(t – 1)
Thay t = x2 + 6x – 7 ta có
(x2 + 6x – 7 – 8)( x2 + 6x – 7 – 1) = (x2 + 6x – 15)( x2 + 6x – 8)
Vậy (x – 1)(x – 2)(x + 7)(x + 8) + 8 = (x2 + 6x – 15)( x2 + 6x – 8).
Câu 30:
Khai triển (x – 2)2.
 Xem đáp án
Xem đáp án
Ta có:
(x – 2)2 = x2 – 2 . x . 2 + 22 = x2 – 4x + 4
Vậy (x – 2)2 = x2 – 4x + 4.
Câu 31:
Chứng minh với ab ≥ 1 thì \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} \ge \frac{2}{{1 + ab}}\).
 Xem đáp án
Xem đáp án
Ta có: \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} \ge \frac{2}{{1 + ab}}\)
\( \Leftrightarrow \frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} - \frac{2}{{1 + ab}} \ge 0\)
\( \Leftrightarrow \left( {\frac{1}{{1 + {a^2}}} - \frac{1}{{1 + ab}}} \right) + \left( {\frac{1}{{1 + {b^2}}} - \frac{1}{{1 + ab}}} \right) \ge 0\)
\( \Leftrightarrow \frac{{1 + ab - 1 - {a^2}}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)}} + \frac{{1 + ab - 1 - {b^2}}}{{\left( {1 + {b^2}} \right)\left( {1 + ab} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{ab - {a^2}}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)}} + \frac{{ab - {b^2}}}{{\left( {1 + {b^2}} \right)\left( {1 + ab} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{\left( {ab - {a^2}} \right)\left( {1 + {b^2}} \right) + \left( {1 + {a^2}} \right)\left( {ab - {b^2}} \right)}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{a\left( {b - a} \right)\left( {1 + {b^2}} \right) + \left( {1 + {a^2}} \right)b\left( {a - b} \right)}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{\left( {b - a} \right)\left[ {a\left( {1 + {b^2}} \right) - b\left( {1 + {a^2}} \right)} \right]}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{\left( {b - a} \right)\left[ {a + a{b^2} - b - {a^2}b} \right]}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{\left( {b - a} \right)\left[ {\left( {a - b} \right) - ab\left( {a - b} \right)} \right]}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{{{\left( {b - a} \right)}^2}\left( {ab - 1} \right)}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\)
Vì ab ≥ 1 nên ab – 1 ≥ 0
Mà (b – a)2 ≥ 0
Suy ra (b – a)2(ab – 1) ≥ 0
Vì (a2 + 1) > 0, (b2 + 1) > 0, (ab + 1) > 0
Nên (a2 + 1)(b2 + 1)(ab + 1) > 0
Suy ra \(\frac{{{{\left( {b - a} \right)}^2}\left( {ab - 1} \right)}}{{\left( {1 + {a^2}} \right)\left( {1 + ab} \right)\left( {1 + {b^2}} \right)}} \ge 0\) với mọi a, b, ab ≥ 1
Vậy \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} \ge \frac{2}{{1 + ab}}\).
Câu 32:
Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng:
\(\frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\).
 Xem đáp án
Xem đáp án
Đặt x = b + c – a
y = a + c – b
z = a + b – c
Suy ra \(\left\{ \begin{array}{l}x + z = b + c - a + a + b - c = 2b\\x + y = b + c - a + a + c - b = 2c\\y + z = a + c - b + a + b - c = 2{\rm{a}}\end{array} \right.\)
Ta có: \(2A = \frac{{y + z}}{x} + \frac{{x + z}}{y} + \frac{{x + y}}{z}\)
\( = \frac{y}{x} + \frac{z}{x} + \frac{x}{y} + \frac{z}{y} + \frac{x}{z} + \frac{y}{z}\)
\( = \left( {\frac{y}{x} + \frac{x}{y}} \right) + \left( {\frac{z}{y} + \frac{y}{z}} \right) + \left( {\frac{x}{z} + \frac{z}{x}} \right)\)
Áp dụng bất đẳng thức Cô – si ta có:
\(\begin{array}{l}\left( {\frac{y}{x} + \frac{x}{y}} \right) \ge 2\sqrt {\frac{y}{x}.\frac{x}{y}} = 2\\\left( {\frac{z}{y} + \frac{y}{z}} \right) \ge 2\sqrt {\frac{z}{y}.\frac{y}{z}} = 2\\\left( {\frac{x}{z} + \frac{z}{x}} \right) \ge 2\sqrt {\frac{z}{x}.\frac{x}{z}} = 2\end{array}\)
Suy ra:
\(\left( {\frac{y}{x} + \frac{x}{y}} \right) + \left( {\frac{z}{y} + \frac{y}{z}} \right) + \left( {\frac{x}{z} + \frac{z}{x}} \right) \ge 6\)
\( \Leftrightarrow 2A = \frac{{y + z}}{x} + \frac{{x + z}}{y} + \frac{{x + y}}{z} \ge 6\)
\( \Leftrightarrow 2A = \frac{{2{\rm{a}}}}{{b + c - a}} + \frac{{2b}}{{a + c - b}} + \frac{{2c}}{{a + b - c}} \ge 6\)
\( \Leftrightarrow A = \frac{{\rm{a}}}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\)
Vậy \(\frac{a}{{b + c - a}} + \frac{b}{{a + c - b}} + \frac{c}{{a + b - c}} \ge 3\).
Câu 33:
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. Gọi I và J lần lượt là trung điểm của MP và NQ. Chứng minh IJ song song với AE và \[{\rm{IJ}} = \frac{1}{4}A{\rm{E}}\].
 Xem đáp án
Xem đáp án
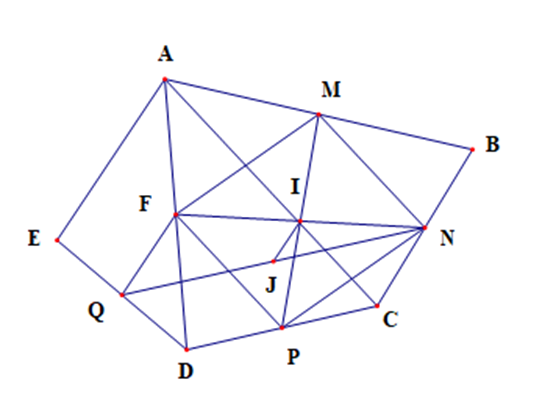
Gọi F là trung điểm của AD
Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, BC
Suy ra MN là đường trung bình
Do đó \(\left\{ \begin{array}{l}MN//AC\\MN = \frac{1}{2}AC\end{array} \right.\) (1)
Xét tam giác ADC có
P, F lần lượt là trung điểm của CD, AD
Suy ra PF là đường trung bình
Do đó \(\left\{ \begin{array}{l}PF//AC\\PF = \frac{1}{2}AC\end{array} \right.\) (2)
Từ (1) và (2) suy ra MN // PF và MN = PF
Do đó MNPF là hình bình hành
Suy ra MP cắt FN tại trung điểm của mỗi đường
Mà I là trung điểm của MP
Suy ra I là trung điểm của FN
Xét tam giác NFQ có
I và J lần lượt là trung điểm của FN và NQ
Suy ra IJ là đường trung bình
Do đó IJ // QF và \[{\rm{IJ}} = \frac{1}{2}FQ\]
Xét tam giác AED có
F và Q lần lượt là trung điểm của AD và ED
Suy ra FQ là đường trung bình
Do đó AE // QF và \[FQ = \frac{1}{2}A{\rm{E}}\]
Mà IJ // QF (chứng minh trên)
Suy ra IJ // AE
Ta có \[{\rm{IJ}} = \frac{1}{2}FQ = \frac{1}{2}.\frac{1}{2}A{\rm{E}} = \frac{1}{4}A{\rm{E}}\]
Vậy IJ // AE và \[{\rm{IJ}} = \frac{1}{4}A{\rm{E}}\].
Câu 34:
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:
a) AB2 = BH . BC
b) AC2 = CH . BC
c) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).
 Xem đáp án
Xem đáp án
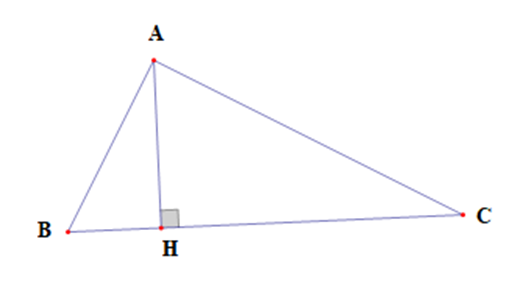
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {AHB} = 90^\circ \)
\(\widehat B\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{AB}}{{BH}} = \frac{{BC}}{{AB}}\)
Suy ra AB2 = BH . BC
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat {BAC} = \widehat {AHC} = 90^\circ \)
\(\widehat C\) là góc chung
Suy ra (g.g)
Do đó \(\frac{{AC}}{{CH}} = \frac{{BC}}{{AC}}\)
Suy ra AC2 = BC . CH
c) Vì (chứng minh câu a)
Nên \(\frac{{AH}}{{AC}} = \frac{{AB}}{{BC}}\)
Suy ra \(\frac{{A{H^2}}}{{A{C^2}}} = \frac{{A{B^2}}}{{B{C^2}}}\) (1)
Vì (chứng minh câu b)
Nên \(\frac{{BC}}{{AC}} = \frac{{AB}}{{AH}}\)
Suy ra \(\frac{{A{H^2}}}{{A{B^2}}} = \frac{{A{C^2}}}{{B{C^2}}}\) (2)
Từ (1) và (2) suy ra \(\frac{{A{H^2}}}{{A{C^2}}} + \frac{{A{H^2}}}{{A{B^2}}} = \frac{{A{B^2}}}{{B{C^2}}} + \frac{{A{C^2}}}{{B{C^2}}} = \frac{{A{B^2} + A{C^2}}}{{B{C^2}}}\)
Mà tam giác ABC vuông tại A nên BC2 = AB2 + AC2
Do đó \(\frac{{A{H^2}}}{{A{C^2}}} + \frac{{A{H^2}}}{{A{B^2}}} = 1\)
Suy ra \(\frac{1}{{A{C^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{A{H^2}}}\)
Vậy \(\frac{1}{{A{C^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{A{H^2}}}\).
Câu 35:
Chứng minh với x, y, z dương ta có \(\frac{{{x^3}}}{{yz}} + \frac{{{y^3}}}{{xz}} + \frac{{{z^3}}}{{xy}} \ge x + y + z\).
 Xem đáp án
Xem đáp án
Ta có:
\(\frac{{{x^3}}}{{yz}} + \frac{{{y^3}}}{{xz}} + \frac{{{z^3}}}{{xy}} = \frac{{{x^4}}}{{xyz}} + \frac{{{y^4}}}{{xyz}} + \frac{{{z^4}}}{{xyz}} = \frac{{{x^4} + {y^4} + {z^4}}}{{xyz}}\)
Áp dụng bất đẳng thức \({a^2} + {b^2} + {c^2} \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{3}\) ta có
\[{{\rm{x}}^4} + {y^4} + {z^4} \ge \frac{{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2}}}{3}\]
Suy ra \(\frac{{{x^4} + {y^4} + {z^4}}}{{xyz}} \ge \frac{{{{\left( {{x^2} + {y^2} + {z^2}} \right)}^2}}}{{3xyz}} \ge \frac{{{{\left[ {\frac{{{{\left( {x + y + z} \right)}^2}}}{3}} \right]}^2}}}{{\frac{{{{\left( {x + y + z} \right)}^3}}}{{3.3}}}}\)
\(\frac{{{x^4} + {y^4} + {z^4}}}{{xyz}} \ge \frac{{{{\left( {x + y + z} \right)}^4}}}{{{{\left( {x + y + z} \right)}^3}}} = x + y + z\)
Do đó \(\frac{{{x^3}}}{{yz}} + \frac{{{y^3}}}{{xz}} + \frac{{{z^3}}}{{xy}} \ge x + y + z\)
Vậy \(\frac{{{x^3}}}{{yz}} + \frac{{{y^3}}}{{xz}} + \frac{{{z^3}}}{{xy}} \ge x + y + z\).
Câu 36:
Với a, b, c là các số dương, chứng minh rằng
\(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).
 Xem đáp án
Xem đáp án
Ta có:
\(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) = 1 + \frac{a}{b} + \frac{a}{c} + 1 + \frac{b}{a} + \frac{b}{c} + 1 + \frac{c}{a} + \frac{c}{b}\)
\( = 3 + \left( {\frac{a}{b} + \frac{b}{a}} \right) + \left( {\frac{c}{b} + \frac{b}{c}} \right) + \left( {\frac{a}{c} + \frac{c}{a}} \right)\)
Áp dụng bất đẳng thức Cô – si ta có
\(\frac{a}{b} + \frac{b}{a} \ge 2\sqrt {\frac{a}{b}.\frac{b}{a}} = 2\)
\(\frac{c}{b} + \frac{b}{c} \ge 2\sqrt {\frac{c}{b}.\frac{b}{c}} = 2\)
\(\frac{a}{c} + \frac{c}{a} \ge 2\sqrt {\frac{a}{c}.\frac{c}{a}} = 2\)
Suy ra \(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 3 + 2 + 2 = 9\)
Vậy \(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).
Câu 37:
Tìm giá trị nhỏ nhất của x2 + 3x + 4.
 Xem đáp án
Xem đáp án
Ta có: x2 + 3x + 4
\( = \left( {{x^2} + 2.x.\frac{3}{2} + \frac{9}{4}} \right) + \frac{7}{4}\)
\( = {\left( {x + \frac{3}{2}} \right)^2} + \frac{7}{4}\)
Vì \({\left( {x + \frac{3}{2}} \right)^2} \ge 0;\forall x\)
Nên \({\left( {x + \frac{3}{2}} \right)^2} + \frac{7}{4} \ge \frac{7}{4};\forall x\)
Dấu “ = ” xảy ra khi \[{\rm{x}} + \frac{3}{2} = 0 \Leftrightarrow x = \frac{{ - 3}}{2}\]
Vậy giá trị nhỏ nhất của x2 + 3x + 4 là \(\frac{7}{4}\) khi \[x = \frac{{ - 3}}{2}\].
Câu 38:
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
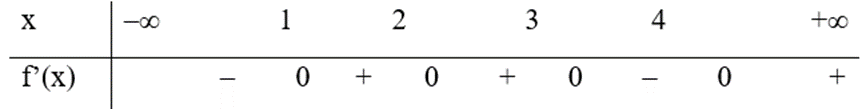
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: y’ > 0 ⇔ 3f’(x + 2) – 3x2 + 3 > 0
⇔ 3f’(x + 2) > 3x2 – 3
⇔ f’(x + 2) > x2 – 1
Đặt t = x + 2, suy ra x = t – 2.
Khi đó f’(t) > (t – 2)2 – 1
Chọn t sao cho \(\left\{ \begin{array}{l}{\left( {t - 2} \right)^2} - 1 < 0\\f'\left( t \right) > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 1 < t - 2 < 1\\t \in \left( {1;2} \right) \cup \left( {2;3} \right) \cup \left( {4; + \infty } \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 < t < 3\\t \in \left( {1;2} \right) \cup \left( {2;3} \right) \cup \left( {4; + \infty } \right)\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}1 < t < 2\\2 < t < 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}1 < x + 2 < 2\\2 < x + 2 < 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\0 < x < 1\end{array} \right.\)
Suy ra hàm số đã cho đồng biến trên khoảng (–1; 0) và (0; 1).
Vậy ta chọn đáp án C.
Câu 39:
Tổng các nghiệm của phương trình 3x+1 + 31-x = 10.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
\[{3^{x + 1}} + {3^{1 - x}} = 10\]
\( \Leftrightarrow {3.3^x} + \frac{3}{{{3^x}}} = 10\)
\( \Leftrightarrow 3.{\left( {{3^x}} \right)^2} + 3 = {10.3^x}\)
\( \Leftrightarrow 3.{\left( {{3^x}} \right)^2} - {10.3^x} + 3 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{3^x} = 3\\{3^x} = \frac{1}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Tổng các nghiệm của phương trình là: 1 + (–1) = 0.
Vậy ta chọn đáp án D.
Câu 40:
Rút gọn các phân thức sau:
a) \(\frac{{{y^3} - {x^3}}}{{{x^3} - 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} - {y^3}}}\)
b) \(\frac{{{x^5} + x + 1}}{{{x^3} + {x^2} + x}}\)
c) \(\frac{{2{{\rm{x}}^2} - x - 3}}{{{x^2} - 4x - 5}}\).
 Xem đáp án
Xem đáp án
a) Ta có:
\(\frac{{{y^3} - {x^3}}}{{{x^3} - 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} - {y^3}}}\)
\( = \frac{{(y - x)\left( {{y^2} + xy + {x^2}} \right)}}{{{{(x - y)}^3}}}\)
\( = - \frac{{{x^2} + xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}\)
b) Ta có: \(\frac{{{x^5} + x + 1}}{{{x^3} + {x^2} + x}}\)
\( = \frac{{\left( {{x^5} - {x^2}} \right) + {x^2} + x + 1}}{{x\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{{x^2}\left( {{x^3} - 1} \right) + \left( {{x^2} + x + 1} \right)}}{{x\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{{x^2}(x - 1)\left( {{x^2} + x + 1} \right) + \left( {{x^2} + x + 1} \right)}}{{x\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{\left( {{x^2} + x + 1} \right)\left( {{x^3} - {x^2} + 1} \right)}}{{x\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{{x^3} - {x^2} + 1}}{x}\)
c) Ta có:
\(\frac{{2{{\rm{x}}^2} - x - 3}}{{{x^2} - 4{\rm{x}} - 5}}\)
\( = \frac{{2{x^2} + 2x - 3x - 3}}{{{x^2} + x - 5x - 5}}\)
\( = \frac{{2x\left( {x + 1} \right) - 3\left( {x + 1} \right)}}{{x\left( {x + 1} \right) - 5\left( {x + 1} \right)}}\)
\( = \frac{{\left( {x + 1} \right)\left( {2x - 3} \right)}}{{\left( {x + 1} \right)\left( {x - 5} \right)}}\)
\( = \frac{{2x - 3}}{{x - 5}}\)
Câu 41:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB.
a) Tìm giao tuyến của (SAC) và (SBD)
b) Tìm giao điểm DN với (SAC)
c) Chứng minh MN // (SCD).
 Xem đáp án
Xem đáp án
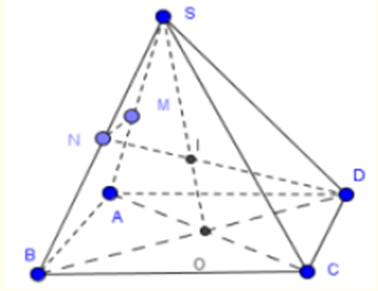
a) Gọi giao điểm của AC và DB là O
Vì O ∈ AC ⊂ (SAC) nên O ∈ (SAC)
O ∈ BD ⊂ (SBD) nên O ∈ (SBD)
Suy ra O ∈ (SAC) ∩ (SBD)
Mà S ∈ (SAC) ∩ (SBD)
Suy ra SO ∈ (SAC) ∩ (SBD)
b) Gọi I là giao điểm của SO và DN
Ta có:
DN ⊂ (SBD)
SO = (SAC) ∩ (SBD)
Suy ra I = DN ∩ (SAC)
c) Xét tam giác SAB có M, N lần lượt là trung điểm của SA, SB
Suy ra MN là đường trung bình
Do đó MN // AB
Mà AB // CD (vì ABCD là hình bình hành)
Suy ra MN // CD
Lại có CD ⊂ (SCD)
Do đó MN // (SCD)
Vậy MN // (SCD).
Câu 42:
Mệnh đề nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ nên nó cùng phương với mọi vectơ
Vậy ta chọn đáp án A.
Câu 43:
Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm hạng tử:
x2 – 2x – 4y2 – 4y.
 Xem đáp án
Xem đáp án
Ta có:
x2 – 2x – 4y2 – 4y
= (x2 – 4y2) – (2x + 4y)
= (x – 2y)(x + 2y) – 2(x + 2y)
= (x + 2y)(x – 2y – 2)
Vậy x2 – 2x – 4y2 – 4y = (x + 2y)(x – 2y – 2).
Câu 44:
Phân tích đa thức thành nhân tử: x3 – 7x – 6.
 Xem đáp án
Xem đáp án
Ta có: x3 – 7x – 6
= x3 – x2 + x2 – x – 6x – 6
= x2(x – 1) + x(x – 1) – 6(x + 1)
= (x – 1)(x2 + x) – 6(x + 1)
= (x – 1)x(x + 1) – 6(x + 1)
= (x + 1)(x2 – x – 6)
= (x + 1)(x2 – 3x + 2x – 6)
= (x + 1)[x(x – 3) + 2(x – 6)]
= (x + 1)(x – 3)(x + 2)
Vậy x3 – 7x – 6 = (x + 1)(x – 3)(x + 2).
Câu 45:
Chứng minh \(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} \ge \frac{3}{{1 + abc}}\) với a, b, c ≥ 1.
 Xem đáp án
Xem đáp án
Ta có:
\(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} \ge \frac{3}{{1 + abc}}\)
\( \Leftrightarrow \frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} + \frac{1}{{1 + abc}} \ge \frac{4}{{1 + abc}}\)
Xét \(\frac{1}{{1 + {x^2}}} + \frac{1}{{1 + {y^2}}} \ge \frac{2}{{1 + xy}}\) với x, y ≥ 1
\( \Leftrightarrow \frac{1}{{1 + {x^2}}} + \frac{1}{{1 + {y^2}}} - \frac{2}{{1 + xy}} \ge 0\)
\( \Leftrightarrow \frac{{\left( {1 + {y^2}} \right)\left( {1 + xy} \right) + \left( {1 + {x^2}} \right)\left( {1 + xy} \right) - 2\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)\left( {1 + xy} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{1 + xy + {y^2} + x{y^3} + 1 + xy + {x^2} + {x^3}y - 2 - 2{{\rm{x}}^2} - 2{y^2} - 2{x^2}{y^2}}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)\left( {1 + xy} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{x{y^3} + 2xy + {x^3}y - {{\rm{x}}^2} - {y^2} - 2{x^2}{y^2}}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)\left( {1 + xy} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{xy\left( {{y^2} - 2{\rm{x}}y + {x^2}} \right) - \left( {{y^2} - 2{\rm{x}}y + {x^2}} \right)}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)\left( {1 + xy} \right)}} \ge 0\)
\( \Leftrightarrow \frac{{{{\left( {x - y} \right)}^2}\left( {xy - 1} \right)}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)\left( {1 + xy} \right)}} \ge 0\)
Vì x, y ≥ 1 nên xy – 1 ≥ 0
Mà (x – y)2 ≥ 0, 1 + x2 > 0, 1 + y2 > 0, xy + 1 > 0
Suy ra \(\frac{{{{\left( {x - y} \right)}^2}\left( {xy - 1} \right)}}{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)\left( {1 + xy} \right)}} \ge 0\) với mọi x, y ≥ 1
Do đó \(\frac{1}{{1 + {x^2}}} + \frac{1}{{1 + {y^2}}} \ge \frac{2}{{1 + xy}}\) với x, y ≥ 1
Áp dụng bất đẳng thức trên ta có:
\(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} + \frac{1}{{1 + abc}} \ge \frac{2}{{1 + \sqrt {{a^3}{b^3}} }} + \frac{2}{{1 + \sqrt {ab{c^4}} }}\)
\( \Leftrightarrow \frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} + \frac{1}{{1 + abc}} \ge \frac{4}{{1 + \sqrt {{a^3}{b^3}\sqrt {ab{c^4}} } }}\)
\( \Leftrightarrow \frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} + \frac{1}{{1 + abc}} \ge \frac{4}{{1 + abc}}\)
Dấu “ = ” xảy ra khi a = b = c = 1
Vậy \(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} \ge \frac{3}{{1 + abc}}\) với a, b, c ≥ 1.
Câu 46:
Cho A = 5n+2 + 26 . 5n + 82n + 1. Chứng minh A ⋮ 59.
 Xem đáp án
Xem đáp án
Ta có:
A = 5n+2 + 26 . 5n + 82n + 1
A = 5n . 52 + 26 . 5n + 82n . 8
A = 5n . 25 + 26 . 5n + 82n . 8
A = 5n (25 + 26) + 82n . 8
A = 51 . 5n + 64n . 8
Vì 64 : 59 dư 5 nên 64n : 59 dư 5n
Suy ra 51 . 5n + 64n . 8 chia 59 dư
51 . 5n + 5n . 8 = 5n(51 + 8) = 59 . 5n
Mà 59 . 5n ⋮ 59
Suy ra A ⋮ 59
Vậy A ⋮ 59.
Câu 47:
Cho x > 0, y > 0 và x + y = 1. Chứng minh: \(8\left( {{x^4} + {y^4}} \right) + \frac{1}{{xy}} \ge 5\).
 Xem đáp án
Xem đáp án
Ta có:
(a – b)2 ≥ 0
⇔ a2 – 2ab + b2 ≥ 0
⇔ a2 + b2 ≥ 2ab
⇔ 2(a2 + b2) ≥ 2ab + a2 + b2
⇔ 2(a2 + b2) ≥ (a + b)2
\( \Leftrightarrow {a^2} + {b^2} \ge \frac{{{{\left( {a + b} \right)}^2}}}{2}\)
Áp dụng bất đẳng thức trên ta có
\(8\left( {{x^4} + {y^4}} \right) \ge 8\left[ {\frac{{{{\left( {{x^2} + {y^2}} \right)}^2}}}{2}} \right]\)
\( \Leftrightarrow 8\left( {{x^4} + {y^4}} \right) \ge 4{\left( {{x^2} + {y^2}} \right)^2}\)
\( \Leftrightarrow 8\left( {{x^4} + {y^4}} \right) \ge 4{\left[ {\frac{{\left( {x + {y^2}} \right)}}{2}} \right]^2} = 1\) (vì x + y = 1)
Lại có (x + y)2 ≥ 4xy
⇔ 1 ≥ 4xy (vì x + y = 1)
\( \Leftrightarrow xy \le \frac{1}{4}\)
\( \Leftrightarrow \frac{1}{{xy}} \ge 4\)
Suy ra \(8\left( {{x^4} + {y^4}} \right) + \frac{1}{{xy}} \ge 1 + 4 = 5\)
Vậy \(8\left( {{x^4} + {y^4}} \right) + \frac{1}{{xy}} \ge 5\).
Câu 48:
Chứng minh rằng a4 + b4 + c4 ≥ abc(a + b + c).
 Xem đáp án
Xem đáp án
Áp dụng bất đẳng thức Cô – si cho 4 số ta có:
\({a^4} + {a^4} + {b^4} + {c^4} \ge 4\sqrt[4]{{{a^4}.{a^4}.{b^4}.{c^4}}} = 4{{\rm{a}}^2}bc\)
\({a^4} + {b^4} + {b^4} + {c^4} \ge 4\sqrt[4]{{{a^4}.{b^4}.{b^4}.{c^4}}} = 4{\rm{a}}{b^2}c\)
\({a^4} + {b^4} + {c^4} + {c^4} \ge 4\sqrt[4]{{{a^4}.{b^4}.{c^4}.{c^4}}} = 4{\rm{a}}b{c^2}\)
Cộng vế của các bất đẳng thức ta có:
4(a4 + b4 + c4) ≥ 4(a2bc + ab2c + abc2)
⇔ a4 + b4 + c4 ≥ abc(a + b + c)
Vậy a4 + b4 + c4 ≥ abc(a + b + c).
