Cho a là số thực dương, a ≠ 1 và \(P = {\log _{\sqrt[3]{a}}}{a^3}\). Mệnh đề nào dưới đây đúng?
A. P = 3
B. P = 1
C. P = 9
D. \(P = \frac{1}{3}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Ta có:
\(P = {\log _{\sqrt[3]{a}}}{a^3} = {\log _{{a^{\frac{1}{3}}}}}{a^3} = 3.3{\log _a}a = 9\,\,\left( {a > 0,a \ne 1} \right)\)
Vậy ta chọn đáp án C.
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
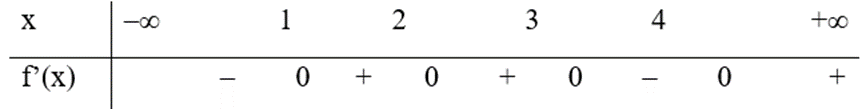
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
Hình bình hành ABCD có AC ⊥ AD và AD = 3,5; \(\widehat D = 50^\circ \). Tính diện tích ABCD.
Cho hàm số f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x2 – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?
Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
Tìm tất cả các giá trị của tham số m để hàm số y = x3 + x2 + mx + 1 đồng biến trên khoảng (–∞; +∞)
Với a, b, c là các số dương, chứng minh rằng
\(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).
Chứng minh \(\frac{1}{{1 + {a^3}}} + \frac{1}{{1 + {b^3}}} + \frac{1}{{1 + {c^3}}} \ge \frac{3}{{1 + abc}}\) với a, b, c ≥ 1.
Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:
a) AB2 = BH . BC
b) AC2 = CH . BC
c) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\).