Cho Ax, By là các tiếp tuyến của \(\left( {O;\frac{{AB}}{2}} \right)\). Tiếp tuyến tại M của (O) cắt Ax, By, AB lần lượt tại C, D, E. AD và BC cắt nhau tại N
a) Tính AC. BD theo AB
b) Chứng minh MN vuông góc AB
c) So sánh 2 tỉ số \(\frac{{CM}}{{CE}};\frac{{DM}}{{DE}}\).
d) Chứng minh rằng đường thẳng EN đi qua trung điểm của các đoạn thẳng AC, BD.
Giải bởi Vietjack
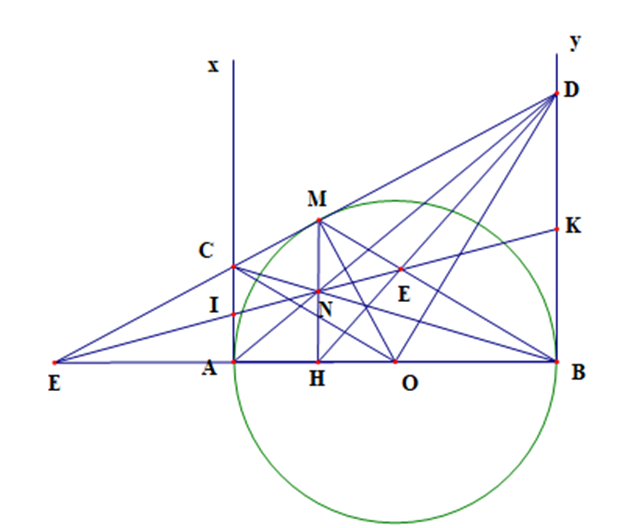
a) Xét (O) có CA, CM là hai tiếp tuyến cắt nhau tại C
Suy ra CA = CM, OC là tia phân giác của \(\widehat {AOM}\)
Do đó \(\widehat {COM} = \frac{1}{2}\widehat {AOM}\)
Xét (O) có DB, DM là hai tiếp tuyến cắt nhau tại D
Suy ra DB = DM, OD là tia phân giác của \(\widehat {BOM}\)
Do đó \(\widehat {DOM} = \frac{1}{2}\widehat {BOM}\)
Ta có: \(\widehat {COD} = \widehat {COM} + \widehat {DOM} = \frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.180^\circ = 90^\circ \)
Do đó tam giác COD vuông tại O
Mà OM ⊥ CD
Suy ra OM2 = CM . DM (hệ thức lượng trong tam giác vuông)
Mà CA = CM, DB = DM, \(OM = \frac{1}{2}AB\)
Suy ra \(CA.DB = \frac{{A{B^2}}}{4}\)
b) Vì AC // BD nên \(\frac{{AC}}{{B{\rm{D}}}} = \frac{{AN}}{{N{\rm{D}}}} = \frac{{CN}}{{NB}}\)
Mà CA = CM, DB = DM (chứng minh câu a)
Suy ra \(\frac{{CM}}{{DM}} = \frac{{AN}}{{N{\rm{D}}}}\)
Xét tam giác ACD có \(\frac{{CM}}{{DM}} = \frac{{AN}}{{N{\rm{D}}}}\)
Suy ra MN // CA
Mà AC ⊥ AB
Do đó MN ⊥ AB
c) Xét tam giác ACE vuông tại A có
\[\sin \widehat E = \frac{{CA}}{{CE}}\]
Mà CA = CM
Suy ra \[\sin \widehat E = \frac{{CM}}{{CE}}\] (1)
Xét tam giác EBD vuông tại B có
\[\sin \widehat E = \frac{{B{\rm{D}}}}{{DE}}\]
Mà BD = DM
Suy ra \[\sin \widehat E = \frac{{DM}}{{DE}}\] (2)
Từ (1) và (2) suy ra \(\frac{{CM}}{{CE}} = \frac{{DM}}{{DE}}\)
d) Gọi giao điểm của MN với AB là H
Giao điểm của AN với AC và BD lần lượt là I và K
Xét (O) đường kính AB có MN ⊥ AO
Mà MN cắt AO tại H
Suy ra H là trung điểm của AO
Xét tam giác DBE có MH // BD
Suy ra \(\frac{{MN}}{{DK}} = \frac{{NH}}{{BK}}\)
Do đó \(\frac{{MN}}{{NH}} = \frac{{DK}}{{BK}}\) (3)
Gọi giao điểm của MB và HD là E
Xét tam giác DKE có MN // KD
Suy ra \(\frac{{NH}}{{DK}} = \frac{{NE}}{{EK}}\)
Xét tam giác BKE có MN // BK
Suy ra \(\frac{{NM}}{{BK}} = \frac{{NE}}{{EK}}\)
Mà \(\frac{{NH}}{{DK}} = \frac{{NE}}{{EK}}\)
Do đó \(\frac{{NH}}{{DK}} = \frac{{MN}}{{BK}}\)
Hay \(\frac{{NM}}{{MH}} = \frac{{BK}}{{DK}}\) (4)
Từ (3) và (4) suy ra \(\frac{{DK}}{{BK}} = \frac{{BK}}{{DK}}\)
Do đó DK = BK, MN = NH
Hay EN đi qua trung điểm K của đoạn thẳng BD
Xét tam giác EHM có CA // MH
Suy ra \(\frac{{CI}}{{MN}} = \frac{{AI}}{{NH}}\)
Mà MN = NH
Suy ra CI = AI
Hay EN đi qua trung điểm I của đoạn thẳng AC
Vậy EN đi qua trung điểm của các đoạn thẳng AC, BD.
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
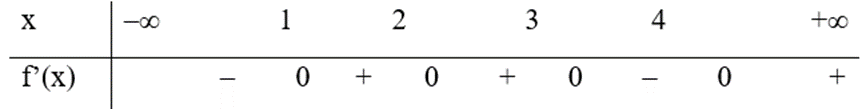
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
Hình bình hành ABCD có AC ⊥ AD và AD = 3,5; \(\widehat D = 50^\circ \). Tính diện tích ABCD.
Cho a là số thực dương, a ≠ 1 và \(P = {\log _{\sqrt[3]{a}}}{a^3}\). Mệnh đề nào dưới đây đúng?
Cho hàm số f(x) có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x2 – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?
Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
Tìm tất cả các giá trị của tham số m để hàm số y = x3 + x2 + mx + 1 đồng biến trên khoảng (–∞; +∞)
Với a, b, c là các số dương, chứng minh rằng
\(\left( {a + b + c} \right)\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right) \ge 9\).
Chứng minh bất đẳng thức sinx < x với mọi x > 0 và sinx > x với mọi x < 0.
