Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có hai điểm cực trị đều nằm bên trái trục tung.
A. 1 < m < 2.
B. m > 1.
C. m < 2.
D. m < 1.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
Ta có: y’ = x2 – 2x + m – 1
Đồ thị hàm số có 2 điểm cực trị đều nằm bên trái trục tung khi y ' = 0 có 2 nghiệm phân biệt đều dương
⇔ Δ ' = 1 − m + 1 > 0
S = 2 > 0
P = m − 1 > 0
(trong đó S là tổng 2 nghiệm và P là tích 2 nghiệm của phương trình)
⇔ 2 > m > 1.
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0.
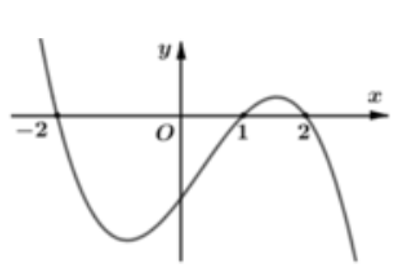
Hàm số g( x) = [f(3 - x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1).
B. (1; 2).
C. (2; 5).
D. ( 5 ; +∞).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Một căn phòng hình chữ nhật có chiều dài 8m, chiều rộng bằng chiều dài. Để lát nền căn phòng đó. Người ta dùng loại gạch men hình vuông cạnh 4dm.
a) Hỏi căn phòng được lát cần bao nhiêu viên gạch đó.
b) Biết rằng để lát 1m2 gạch men hết 75000 đồng. Vậy để lát hết căn phòng đó thì hết bao nhiêu tiền?
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).
Cho a, b, c là các số thực dương thỏa mãn log2a + log8b + log32c = 10 và . Tính log4(abc).