. Giá trị lớn nhất \(M\), nhỏ nhất \(m\) của hàm số \[y = \;\frac{{2{x^2} + 3x + 3}}{{x + 1}}\] trên đoạn \(\left[ {0;2} \right]\) lần lượt là:
B. \(M = \frac{{17}}{3},m = - 3.\)
D. \(M = - 3,m = - 5.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Ta có: \[y = \;\frac{{2{x^2} + 3x + 3}}{{x + 1}}\] \( \Rightarrow y' = \frac{{2{x^2} + 4x}}{{{{\left( {x + 1} \right)}^2}}}\).
\(y' = 0 \Leftrightarrow \frac{{2{x^2} + 4x}}{{{{\left( {x + 1} \right)}^2}}} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ {0;2} \right]\\x = - 2 \notin \left[ {0;2} \right]\end{array} \right.\).
Xét trên đoạn \(\left[ {0;2} \right]\), ta tính được các giá trị \(y\left( 0 \right) = 3,y\left( 2 \right) = \frac{{17}}{3}\).
Vậy \(M = \frac{{17}}{3},m = 3.\)
Trong không gian \[Oxyz\], cho ba điểm \(A(1; - 2;3)\),\(B( - 1;2;5)\),\(C(0;0;1)\).Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\).
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( { - 2;1;2} \right)\), \(\overrightarrow b = \left( {1;1; - 1} \right)\).
a) Xác định tọa độ của \(\overrightarrow u = \overrightarrow a - 2\overrightarrow b \). (0,25 điểm)
b) Tính độ dài của \(\overrightarrow u \). (0,25 điểm)
c) Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). (0,5 điểm)
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(B(1;2 - 3)\), \(C(7;4; - 2)\). Nếu điểm \(E\) thỏa mãn đẳng thức \(\overrightarrow {CE} = 2\overrightarrow {EB} \) thì tọa độ điểm \(E\) là:
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( {2;1; - 1} \right)\),\(\overrightarrow b = \left( {1;3;m} \right)\). Tìm \(m\) để \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \).
Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các suối nước đổ về hồ. Từ lúc 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian \(t\) (giờ) trong ngày cho bởi công thức:
\(h(t) = - \frac{1}{3}{t^3} + 5{t^2} + 24t\), \(\left( {t > 0} \right)\).
Biết rằng phải thông báo cho các hộ dân phải di dời đi trước khi xả nước theo quy định trước 5 giờ. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước mấy giờ? Biết rằng mực nước trong hồ phải đi lên cao nhất mới xả nước. (1,0 điểm)
Trong không gian \[Oxyz\], cho \(\overrightarrow u = \left( { - 1;1;0} \right)\), \(\overrightarrow v = (0; - 1;0)\), góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ.
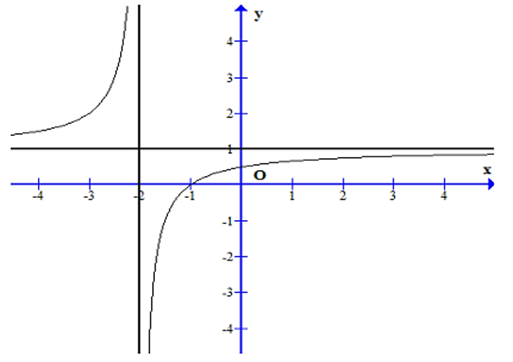
Phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số là:
Cho hàm số \(y = \frac{{4x - 5}}{{x + 1}}\) có đồ thị \(\left( H \right)\). Gọi \(M\left( {{x_0};{y_0}} \right)\) với \({x_0} < 0\) là một điểm thuộc đồ thị \(\left( H \right)\) thỏa mãn tổng khoảng cách từ \(M\) đến hai đường tiệm cận của \(\left( H \right)\) đạt giá trị nhỏ nhất bằng \(6\). Tính giá trị của biểu thức \(S = {\left( {{x_0} + {y_0}} \right)^2}\) . (1,0 điểm)
Trong không gian với hệ trục \[Oxyz\], cho \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là:
Trong không gian với hệ trục \[Oxyz\], cho hình hộp \(ABCD.A'B'C'D'\), biết rằng \[A( - 3;0;0),{\rm{ }}B\left( {0;2;0} \right),{\rm{ }}D\left( {0;0;1} \right),{\rm{ }}A'\left( {1;2;3} \right)\]. Tìm tọa độ điểm \[C'\].
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = \frac{{x + {m^2}}}{{x - 1}}\) trên đoạn \(\left[ {2;3} \right]\) bằng \(14\)?
. Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow u = (1; - 4;0)\) và \(\overrightarrow v = ( - 1; - 2;1)\). Vectơ \(\overrightarrow u + 3\overrightarrow v \) có tọa độ là:
Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat {BAC} = \widehat {BAD} = 60^\circ \), \(\widehat {CAD} = 90^\circ \). Gọi \(I\) và \(J\) lần lượt là trung điểm của \(AB\) và \(CD\). Hãy xác định góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \)?
Trong không gian với hệ trục tọa độ \[Oxyz\], điểm thuộc trục \(Ox\)và cách đều hai điểm \(A\left( {4;2; - 1} \right)\) và \(B\left( {2;1;0} \right)\) là:
Trong không gian \[Oxyz\], cho hai điểm \(A\left( {1;2;1} \right)\), \(B\left( {2; - 1;3} \right)\). Tìm điểm \(M\) trên mặt phẳng \[\left( {Oxy} \right)\] sao cho \[M{A^2}--2M{B^2}\] lớn nhất.