Giải bởi Vietjack
Giải bởi Vietjack
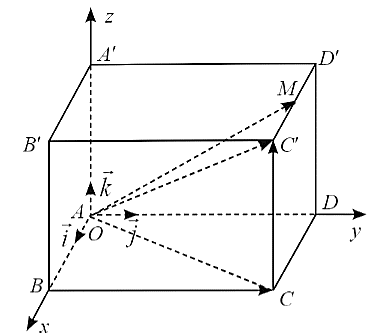
Theo bài ra ta có: \(\overrightarrow {AB} = 14\overrightarrow i + 0\overrightarrow j + 0\overrightarrow k \); \(\overrightarrow {AD} = 0\overrightarrow i + 12\overrightarrow j + 0\overrightarrow k \); \(\overrightarrow {AA'} = 0\overrightarrow i + 0\overrightarrow j + 18\overrightarrow k \).
Vì \(M\) là trung điểm của \(C'D'\) nên
\(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AC'} + \overrightarrow {AD'} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\) (quy tắc hình hộp và quy tắc hình bình hành)
\( = \frac{1}{2}\left( {\overrightarrow {AB} + 2\overrightarrow {AD} + 2\overrightarrow {AA'} } \right)\)
\( = \frac{1}{2}\left[ {14\overrightarrow i + 0\overrightarrow j + 0\overrightarrow k + 2\left( {0\overrightarrow i + 12\overrightarrow j + 0\overrightarrow k } \right) + 2\left( {0\overrightarrow i + 0\overrightarrow j + 18\overrightarrow k } \right)} \right]\)
\( = 7\overrightarrow i + 12\overrightarrow j + 18\overrightarrow k \).
Suy ra \(\overrightarrow {AM} = \left( {7;12;18} \right)\). Do đó, \(a = 7,b = 12,c = 18\).
Vậy \(a + b - c = 7 + 12 - 18 = 1\).
Đáp số: \(1\).
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng \(108\) cm2 như hình dưới đây.
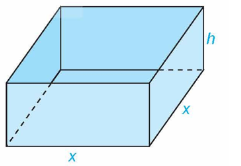
Biết khi \(x = {x_0},\,h = {h_0}\) thì thể tích của hộp là lớn nhất. Khi đó \({x_0} + {h_0}\) bằng bao nhiêu?
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \(\mathbb{R}\) có đồ thị hàm số như hình vẽ dưới đây.
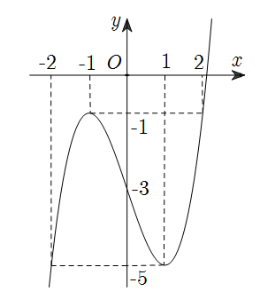
Giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số đã cho trên đoạn \(\left[ { - 2;2} \right]\) lần lượt là:
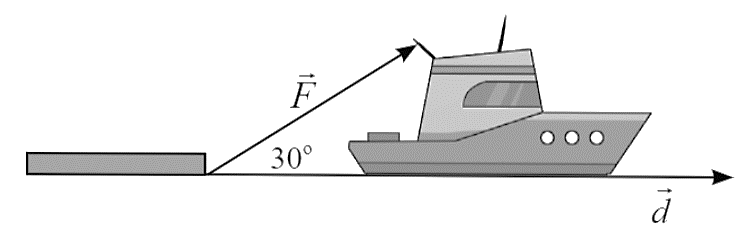
Một tàu kéo một xà lan trên biển di chuyển được 5 km với một lực kéo có cường độ \(3\,000\) N và có phương hợp với phương dịch chuyển một góc \(30^\circ \). Công thực hiện bởi lực kéo nói trên bằng bao nhiêu Jun (làm tròn kết quả đến hàng đơn vị)?
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
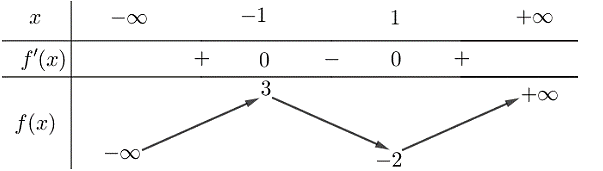
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
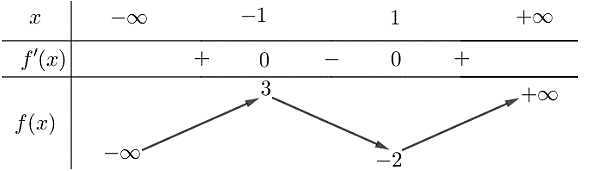
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(1\).
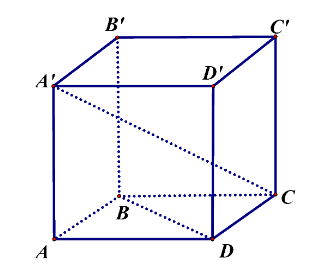
a) \(\overrightarrow {BD} = \overrightarrow {B'D'} \).
b) \(\left| {\overrightarrow {A'C} } \right| = \left| {\overrightarrow {AC'} } \right| = \sqrt 3 \).
c) \(\overrightarrow {A'C} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {D'D} \).
d) \(\overrightarrow {A'C} \cdot \overrightarrow {BD} = \sqrt 2 \).
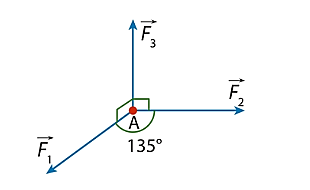
Một chất điểm \(A\) nằm trên mặt phẳng nằm ngang \(\left( \alpha \right)\), chịu tác động bởi ba lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \). Các lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) có giá nằm trong \(\left( \alpha \right)\) và \(\left( {\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} } \right) = 135^\circ \), còn lực \(\overrightarrow {{F_3}} \) có giá vuông góc với \(\left( \alpha \right)\) và hướng lên trên. Độ lớn hợp lực của các lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} \) bằng bao nhiêu (làm tròn kết quả đến hàng phần mười), biết rằng độ lớn của ba lực đó lần lượt là 20 N, 15 N và 10 N.