 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có: \(y = {x^3} - 3x\) \( \Rightarrow y' = 3{x^2} - 3.\)
\(y' = 0 \Leftrightarrow x = \pm 1.\)
Ta có bảng biến thiên như sau:
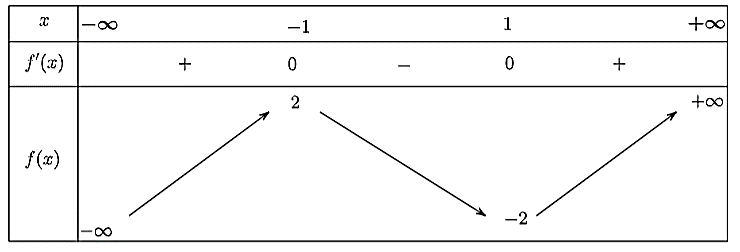
Hàm số \(y = {x^3} - 3x\) nghịch biến trên khoảng \(\left( { - 1;1} \right).\)
Cho hàm số \(\left( C \right)\): \(y = \frac{{{x^2} - 3x + m}}{{x - 1}}.\)
Khảo sát và vẽ đồ thị hàm số \(\left( C \right)\) với \(m = - 4.\)
Hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.
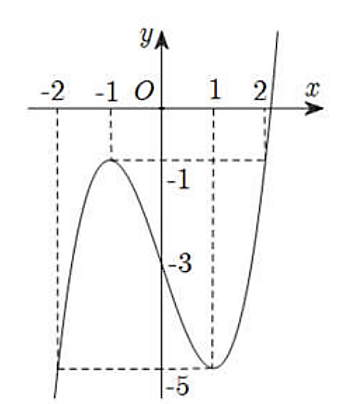
Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;2} \right]\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
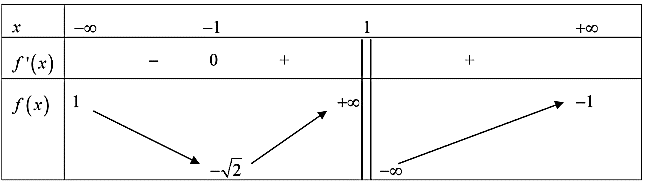
Tập hợp tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt.
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới.
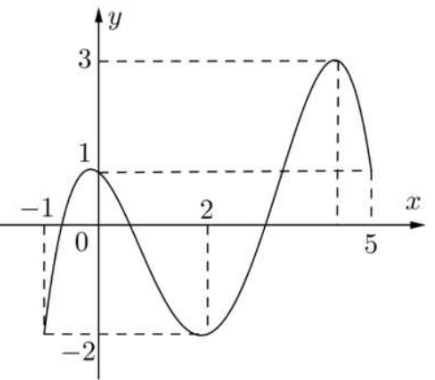
Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\) bằng:
Cho hàm số \(y = f(x)\) liên tục và có đồ thị hàm số trên đoạn \(\left[ { - 2;4} \right]\) như hình vẽ dưới đây.
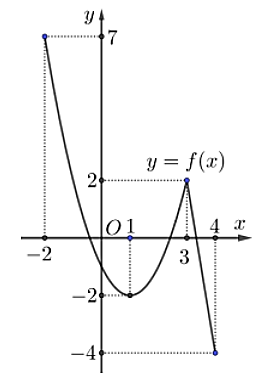
Tổng giá trị lớn nhất và nhỏ nhất của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;4} \right]\) bằng:
Cho hàm số \(\left( C \right)\): \(y = \frac{{{x^2} - 3x + m}}{{x - 1}}.\)
Với \(m = 2\), tính giá trị lớn nhất, giá trị nhỏ nhất của \(\left( C \right)\) trên đoạn \(\left[ {2;3} \right]\).
Cho hàm số \(y = f(x)\) có đồ thị là đường cong trong hình dưới đây.
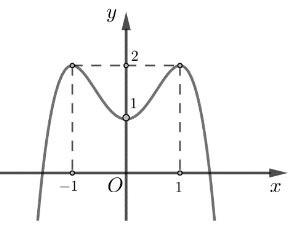
Hàm số đã cho đồng biến trên khoảng nào dưới đây?