Đề thi giữa kì 1 Toán 12 Cánh Diều có đáp án - Đề 10
-
386 lượt thi
-
39 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số \(y = f(x)\) có đồ thị là đường cong trong hình dưới đây.
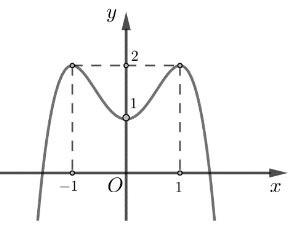
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào đồ thị hàm số \(y = f(x)\) ta có hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right).\)
Câu 2:
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
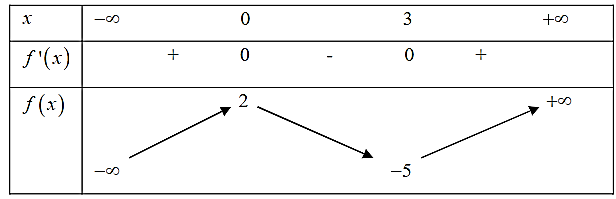
Giá trị cực tiểu của hàm số đã cho bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dựa vào bảng biến thiên ta có giá trị cực tiểu của hàm số bằng \( - 5.\)
Câu 3:
Cho hàm số bậc ba \(y = f(x)\) có đồ thị là đường cong trong hình dưới đây.
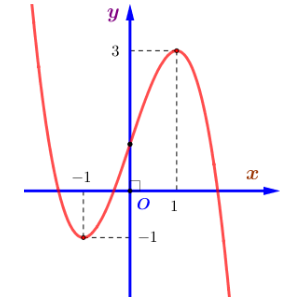
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ đồ thị hàm số \(y = f(x)\), ta có điểm cực tiểu của đồ thị hàm số có tọa độ là \(\left( { - 1; - 1} \right).\)
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(y = {x^3} - 3x\) \( \Rightarrow y' = 3{x^2} - 3.\)
\(y' = 0 \Leftrightarrow x = \pm 1.\)
Ta có bảng biến thiên như sau:
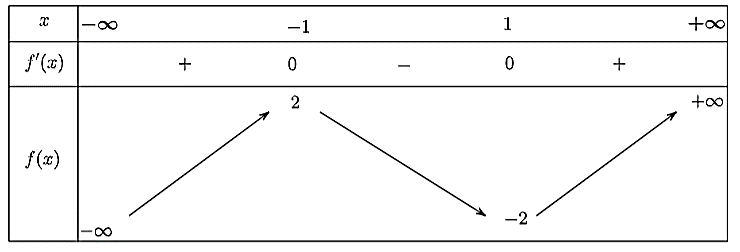
Hàm số \(y = {x^3} - 3x\) nghịch biến trên khoảng \(\left( { - 1;1} \right).\)
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét hàm số \(y = 2\sqrt x - x\):
Tập xác định \(D = \left[ {0; + \infty } \right)\).
Ta có \(y' = \frac{1}{{\sqrt x }} - 1 = \frac{{1 - \sqrt x }}{{\sqrt x }}\), \(\forall x \in \left( {0;\, + \infty } \right)\); \(y' = 0 \Leftrightarrow x = 1\).
Bảng biến thiên của hàm số trên \(D = \left[ {0; + \infty } \right)\) như sau:
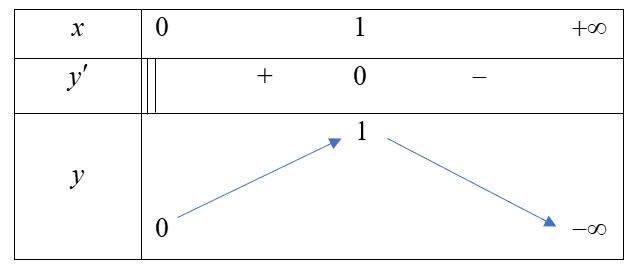
Vậy hàm số đạt cực đại tại \(x = 1\).
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(f\left( x \right) = {x^3} - 3{x^2} + 4\) \( \Rightarrow f'\left( x \right) = 3{x^2} - 6x\).
\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2.\end{array} \right.\)
Ta có bảng biến thiên như sau:
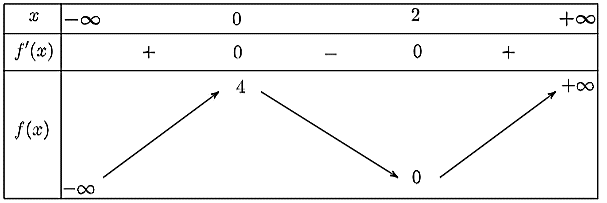
Từ bảng biến thiên, hàm số có giá trị cực đại bằng \(4\) tại \(x = 0\) và đạt giá trị cực tiểu bằng \(0\) tại \(x = 2.\)
Vậy hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số là: \(4 - 0 = 4.\)
Câu 7:
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức sau:
\(G\left( x \right) = 0,025{x^2}\left( {30 - x} \right),\)
trong đó \(x\)là lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam).
Liều lượng thuốc cần tiêm cho bệnh nhân nằm trong khoảng nào để huyết áp bệnh nhân tăng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(G\left( x \right) = 0,025{x^2}\left( {30 - x} \right) = 0,75{x^2} - 0,025{x^3}\), \(\left( {x > 0} \right)\).
\(G'\left( x \right) = 1,5x - 0,075{x^2}\)
\(G'\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 20\end{array} \right.\).
Ta có bảng biến thiên như sau:
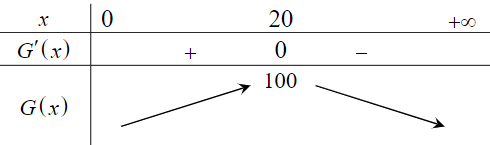
Liều lượng thuốc cần tiêm cho bệnh nhân nằm trong khoảng \(\left( {0;20} \right)\) thì huyết áp bệnh nhân tăng.
Câu 8:
Cho hàm số \(y = f(x)\) liên tục và có đồ thị hàm số trên đoạn \(\left[ { - 2;4} \right]\) như hình vẽ dưới đây.
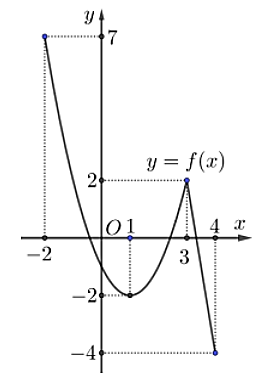
Tổng giá trị lớn nhất và nhỏ nhất của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;4} \right]\) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét trên đoạn \(\left[ { - 2;4} \right]\), hàm số đã cho đạt giá trị lớn nhất bằng \(7\) và đạt giá trị nhỏ nhất bằng \( - 4\).
Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;4} \right]\) bằng\(7 + \left( { - 4} \right) = 3.\)
Câu 9:
Hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ dưới đây.
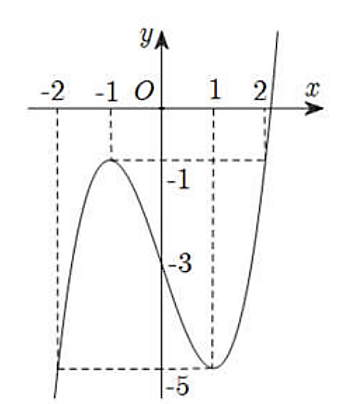
Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 2;2} \right]\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nhìn vào đồ thị ta thấy:
\(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 1\) khi \(x = - 1\) hoặc \(x = 2.\)
\(m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 5\) khi \(x = - 2\) hoặc \(x = 1.\)
Câu 10:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới.
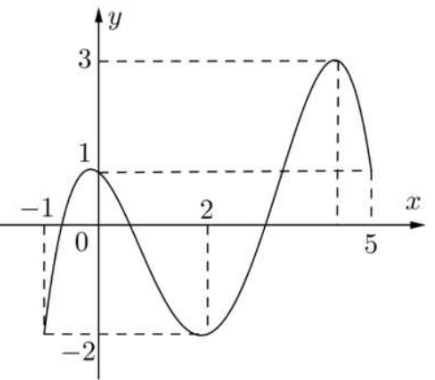
Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ đồ thị hàm số, ta thấy: \(\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 1;5} \right]} f\left( x \right) = 3\\m = \mathop {\min }\limits_{\left[ { - 1;5} \right]} f\left( x \right) = - 2\end{array} \right. \Rightarrow M.m = 3.\left( { - 2} \right) = - 6.\)
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hàm số đã cho liên tục trên \(\left[ {0;3} \right]\).
Ta có \(y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\) với \(\forall x \in \left[ {0;3} \right]\).
Ta được: \(y\left( 0 \right) = - 1,y\left( 3 \right) = \frac{1}{2}\).
Do đó \(\mathop {\min }\limits_{\left[ {0;3} \right]} y = y\left( 0 \right) = - 1.\)
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(f'\left( x \right) = 2\left( {{x^2} - 2} \right){e^{2x}} + 2x{e^{2x}} = 2\left( {{x^2} + x - 2} \right){e^{2x}}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ { - 1;2} \right]\\x = - 2 \notin \left[ { - 1;2} \right]\end{array} \right.\)
Và \(f\left( { - 1} \right) = - {e^{ - 2}};f\left( 2 \right) = 2{e^4};f\left( 1 \right) = - {e^2}.\)
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left( {{x^2} - 2} \right){e^{2x}}\) trên đoạn \(\left[ { - 1;2} \right]\) bằng \( - {e^2}\) tại \(x = 1.\)
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đặt \(t = {\sin ^2}x\), \(0 \le t \le 1\) \( \Rightarrow f\left( t \right) = {t^2} - 4t + 5\)\( \Rightarrow \)\(f'\left( t \right) = 2t - 4\).
\(f'\left( t \right) = 0 \Leftrightarrow t = 2 \notin \left[ {0;1} \right]\).
Ta có: \(f\left( 0 \right) = 5,f\left( 1 \right) = 2\). Vậy \(\mathop {\min }\limits_\mathbb{R} y = 2,\mathop {\max }\limits_\mathbb{R} y = 5\).
Câu 14:
Một chất điểm chuyển động trong \(20\) giây đầu tiên có phương trình như sau:
\(s\left( t \right) = \frac{1}{{12}}{t^4} - {t^3} + 6{t^2} + 10t,\)
trong đó \(t > 0\) với \(t\) tính bằng giây \(\left( s \right)\) và \(s\left( t \right)\) tính bằng mét \(\left( m \right)\). Hỏi tại thời điểm gia tốc đạt giá trị nhỏ nhất thì vận tốc bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vận tốc của chuyển động là: \(v\left( t \right) = s'\left( t \right) = \frac{1}{3}{t^3} - 3{t^2} + 12t + 10.\)
Gia tốc của chuyển động là: \(a\left( t \right) = v'\left( t \right) = {t^2} - 6t + 12 = {\left( {t - 3} \right)^2} + 3.\)
Nhận thấy \({t^2} - 6t + 12 = {\left( {t - 3} \right)^2} + 3 \ge 3\).
Dấu xảy ra khi \(t = 3\).
Vậy gia tốc đạt giá trị nhỏ nhất tại \(t = 3\left( s \right)\).
Khi đó vận tốc của vật bằng: \(v\left( 3 \right) = 28\left( {m/s} \right).\)
Câu 15:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
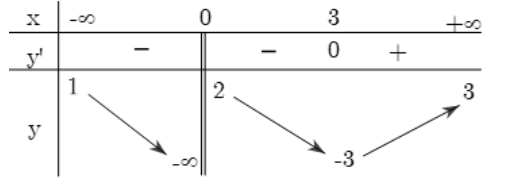
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dựa vào bảng biến thiên, ta có:
\(\mathop {\lim }\limits_{x \to {0^ - }} y = - \infty \) nên \(x = 0\) là đường tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \infty } y = 1\) nên \(y = 1\) là đường tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = 3\) nên \(y = 3\) là đường tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{2x - 2}}{{x + 1}} = - \infty \) và \(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{2x - 2}}{{x + 1}} = + \infty \) nên đường thẳng \(x = - 1\)là tiệm cận đứng của đồ thị hàm số.
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét các đáp án A, B, C, D, ta thấy:
Ở đáp án C, hàm số \(y = \frac{{{x^2}}}{{x + 3}}\) ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = + \infty \\\mathop {\lim }\limits_{x \to - \infty } y = - \infty .\end{array} \right.\)
Do đó đồ thị hàm số \(y = \frac{{{x^2}}}{{x + 3}}\) không có tiệm cận ngang.
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Để đồ thị \(\left( C \right)\) nhận điểm \(I\left( {2;1} \right)\) là tâm đối xứng thì đồ thị \(\left( C \right)\) phải có đường tiệm cận đứng \(x = 2.\)
Do đó \(m + 2 = 0 \Leftrightarrow m = - 2.\)
Câu 19:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên như sau:
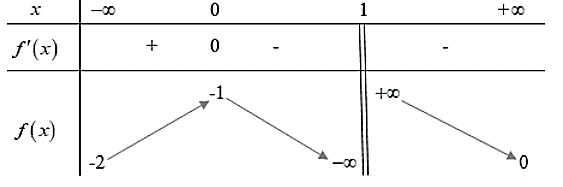
Đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) + 3}}\) có bao nhiêu đường tiệm cận đứng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(y = \frac{1}{{2f\left( x \right) + 3}}\).
Xét \(2f\left( x \right) + 3 = 0 \Leftrightarrow f\left( x \right) = - \frac{3}{2}\).
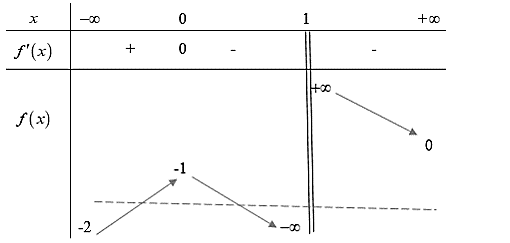
Từ bảng biến thiên nhận thấy phương trình \(f\left( x \right) = - \frac{3}{2}\) có hai nghiệm phân biệt\({x_1} \in \left( { - \infty ;0} \right),\)\({x_2} \in \left( {0;1} \right)\).
Do đó đồ thị hàm số \(y = \frac{1}{{2f\left( x \right) + 3}}\) có hai đường tiệm cận đứng.
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Để đồ thị hàm số không có tiệm cận đứng thì \({x^2} - 2mx + 1 = 0\) vô nghiệm.
Do đó \(\Delta ' = {m^2} - 1 < 0 \Leftrightarrow - 1 < m < 1.\)
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đồ thị hàm số có tiệm cận đứng \({d_1}:x = 1\) và tiệm cận ngang \({d_2}:y = 2.\)
Giả sử \(M\left( {{x_0};\frac{{2{x_0} - 1}}{{{x_0} - 1}}} \right) \in \left( C \right)\) với \({x_0} \ne 1.\)
Ta có: \(d\left( {M,{d_1}} \right) = \left| {{x_0} - 1} \right|\); \(d\left( {M,{d_2}} \right) = \left| {\frac{{2{x_0} - 1}}{{{x_0} - 1}} - 2} \right| = \frac{1}{{\left| {{x_0} - 1} \right|}}.\)
Theo đề bài, ta có: \(\left| {{x_0} - 1} \right| + \frac{1}{{\left| {{x_0} - 1} \right|}} = 2\left| {{x_0} - 1} \right|.\frac{1}{{\left| {{x_0} - 1} \right|}} = 2\).
\( \Leftrightarrow \left| {{x_0} - 1} \right| = 1 \Rightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 0.\end{array} \right.\)
Vậy có hai điểm \(M\) thỏa mãn bài toán.
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y = {x^3} + x + 1\)
\(y' = 3{x^2} + 1 > 0,\forall x \in \mathbb{R}.\)
Vậy hàm số luôn đồng biến trên \(\left( { - \infty ; + \infty } \right).\) Chọn D.
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét hàm số \(y = \frac{{{x^2} + x + 1}}{{x - 1}}\):
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Ta có: \(y = \frac{{{x^2} + x + 1}}{{x - 1}} = x + 2 + \frac{3}{{x - 1}}\)
\(y' = \frac{{{x^2} - 2x - 2}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 3 \\x = 1 + \sqrt 3 \end{array} \right.\).
Đồ thị hàm số có tiệm cận đứng \(x = 1\) và tiệm cận xiên \(y = x + 2.\)
Ta có bảng biến thiên:
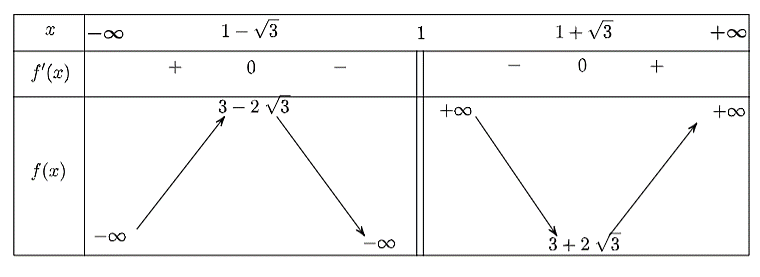
Từ bảng biến thiên, ta thấy hàm số có 2 cực trị.
Quan sát các đồ thị đã cho, ta thấy đồ thị ở phương án A thỏa mãn.
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Thay tọa độ các điểm ở các đáp án A, B, C, D vào hàm số \(y = {x^4} - 2{x^2} - 1\), ta thấy đáp án A thỏa mãn.
Câu 25:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
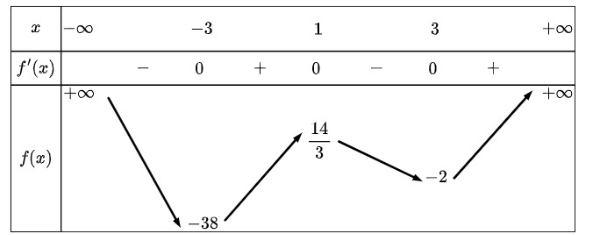
Đồ thị của hàm số trên cắt trục hoành tại mấy điểm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
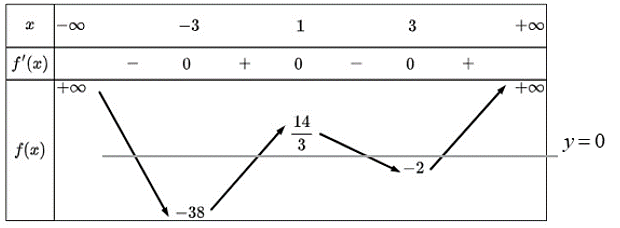
Từ bảng biến thiên, ta thấy đường thẳng \(y = 0\) (trục hoành) cắt đồ thị hàm số đã cho tại 4 điểm.
Câu 26:
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
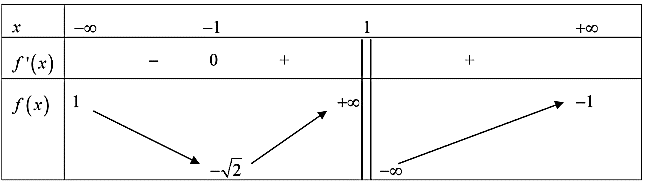
Tập hợp tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
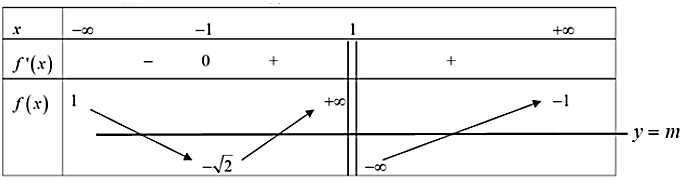
Đường thẳng \(y = m\) cắt đồ thị hàm số đã cho tại 3 điểm phân biệt khi \( - \sqrt 2 < m < - 1.\)
Câu 27:
Hàm số \(y = f'\left( x \right)\) có đồ thị hàm số như hình vẽ.
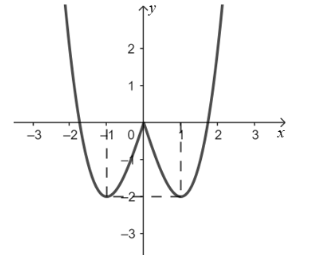
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\), ta có:
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a \in \left( { - 2; - 1} \right)\\x = 0\\x = b \in \left( {1;2} \right).\end{array} \right.\)
Từ đồ thị, ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau:
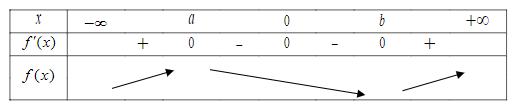
Vậy hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right).\)
Câu 28:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tập xác định: \(D = \mathbb{R}.\)
Ta có: \(y' = 3{x^2} - 4x + m - 1\).
Gọi \(M\left( {{x_0};{y_0}} \right) \in \left( C \right)\) là tiếp điểm.
Phương trình tiếp tuyến tại \(M\): \(y = k\left( {x - {x_0}} \right) + {y_0}.\)
Ta có: \(k = y'\left( {{x_0}} \right) = 3x_0^2 - 4{x_0} + m - 1\)
\(k' = 6{x_0} - 4\)
\(k' = 0 \Leftrightarrow {x_0} = \frac{2}{3} \Rightarrow k = \frac{{ - 7}}{3} + m.\)
Ta có bảng biến thiên sau:
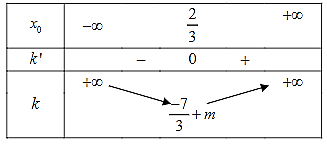
Từ đây, hệ số góc nhỏ nhất của tiếp tuyến của đồ thị \(\left( C \right)\) là \({k_{\min }} = \frac{{ - 7}}{3} + m\).
Tiếp tuyến này vuông góc với đường thẳng \(d:y = 3x + 2024\) khi và chỉ khi
\({k_{\min }} = \frac{{ - 1}}{{{k_d}}} = \frac{{ - 1}}{3}\) \( \Leftrightarrow \frac{{ - 7}}{3} + m = \frac{{ - 1}}{3} \Leftrightarrow m = 2.\)
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
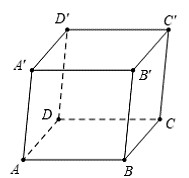
Có 3 vectơ bằng vectơ \(\overrightarrow {BC} \), đó là: \(\overrightarrow {AD} ,\overrightarrow {A'D'} ,\overrightarrow {B'C'} \).
Câu 30:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
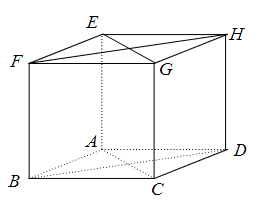
Ta có: \(EG\,{\rm{//}}\,AC\) (do \(ACGE\) là hình chữ nhật).
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = 45^\circ .\)
Câu 31:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right).\)
Mà theo giả thiết, ta có: \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\) \( \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 1 \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 180^\circ .\)
Câu 32:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
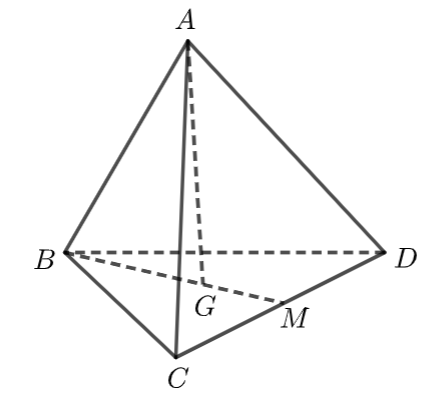
Gọi \(M\) là trung điểm \(CD\) \( \Rightarrow \overrightarrow {BG} = \frac{2}{3}\overrightarrow {BM} .\)
Ta có: \(\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BM} = \overrightarrow {AB} + \frac{2}{3}.\frac{1}{2}.\left( {\overrightarrow {BC} + \overrightarrow {BD} } \right).\)
\( = \overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} + \overrightarrow {AD} - \overrightarrow {AB} } \right)\)
\( = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right) = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right).\)
Câu 33:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
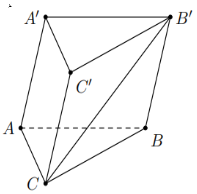
Vì \(BB'C'C\) là hình bình hành nên
\(\overrightarrow {B'C} = \overrightarrow {B'C'} + \overrightarrow {B'B} = \overrightarrow {BC} - \overrightarrow {AA'} .\)
\( = - \overrightarrow {AA'} + \overrightarrow {BA} + \overrightarrow {AC} \)
\( = - \overrightarrow {AA'} - \overrightarrow {AB} + \overrightarrow {AC} \)
\( = - \overrightarrow a - \overrightarrow b + \overrightarrow c .\)
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
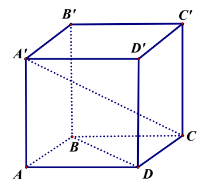
Ta có: \(\overrightarrow {A'C} .\overrightarrow {BD} = \left( {\overrightarrow {A'B'} + \overrightarrow {A'D'} + \overrightarrow {A'A} } \right).\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)
\[ = \overrightarrow {A'B'} .\overrightarrow {AD} - \overrightarrow {A'B'} .\overrightarrow {AB} + \overrightarrow {A'D'} .\overrightarrow {AD} - \overrightarrow {A'D'} .\overrightarrow {AB} + \overrightarrow {A'A} .\overrightarrow {AD} - \overrightarrow {A'A} .\overrightarrow {AB} \]
\( = 0 - {\left( {\overrightarrow {AB} } \right)^2} + {\left( {\overrightarrow {AD} } \right)^2} - 0 + 0 - 0 = 0\).
(Vì \(ABCD\) là hình vuông nên \(AB = AD\)).
Vậy \(\overrightarrow {A'C} \bot \overrightarrow {BD} \) hay góc giữa \(\overrightarrow {A'C} \) và \(\overrightarrow {BD} \) bằng \(90^\circ .\)
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
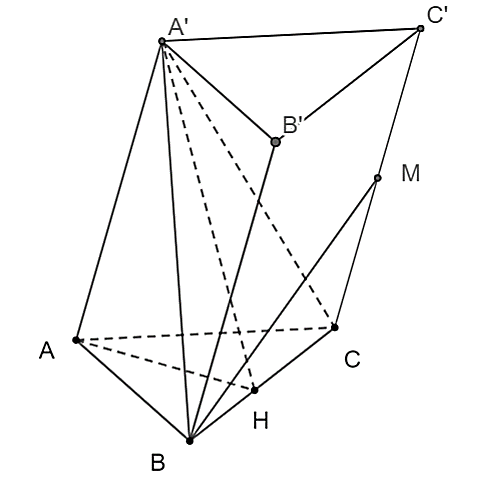
Gọi \(H\) là trung điểm của \(BC\).
Ta có: \(AH = A'H = \frac{{a\sqrt 3 }}{2}\) và \(AH \bot BC,A'H \bot BC\) \( \Rightarrow BC \bot \left( {AA'H} \right) \Rightarrow BC \bot AA'\) hay \(BC \bot BB'\). Do đó, \(BCC'B'\) là hình chữ nhật.
Khi đó, \(CC' = AA' = \frac{{a\sqrt 3 }}{2}.\sqrt 2 = \frac{{a\sqrt 6 }}{2}\) \( \Rightarrow BM = \sqrt {{a^2} + \frac{{{a^2}.6}}{{16}}} = \frac{{a\sqrt {22} }}{4}\).
Xét \(\overrightarrow {AA'} .\overrightarrow {BM} = \overrightarrow {AA'} .\left( {\overrightarrow {BC} + \overrightarrow {CM} } \right) = \overrightarrow {AA'} .\overrightarrow {BC} + \overrightarrow {AA'} .\overrightarrow {CM} = 0 + \left| {\overrightarrow {AA'} } \right|.\left| {\overrightarrow {CM} } \right|.\cos 0^\circ = \frac{{3{a^2}}}{4}.\)
Suy ra \(\cos \alpha = \cos \left( {\overrightarrow {AA'} ,\overrightarrow {BM} } \right) = \frac{{\overrightarrow {AA'} .\overrightarrow {BM} }}{{\left| {\overrightarrow {AA'} } \right|.\left| {\overrightarrow {BM} } \right|}} = \frac{{\frac{{3{a^2}}}{4}}}{{\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt {22} }}{4}}} = \frac{{\sqrt {33} }}{{11}}.\)
Câu 36:
Cho hàm số \(\left( C \right)\): \(y = \frac{{{x^2} - 3x + m}}{{x - 1}}.\)
Khảo sát và vẽ đồ thị hàm số \(\left( C \right)\) với \(m = - 4.\)
 Xem đáp án
Xem đáp án
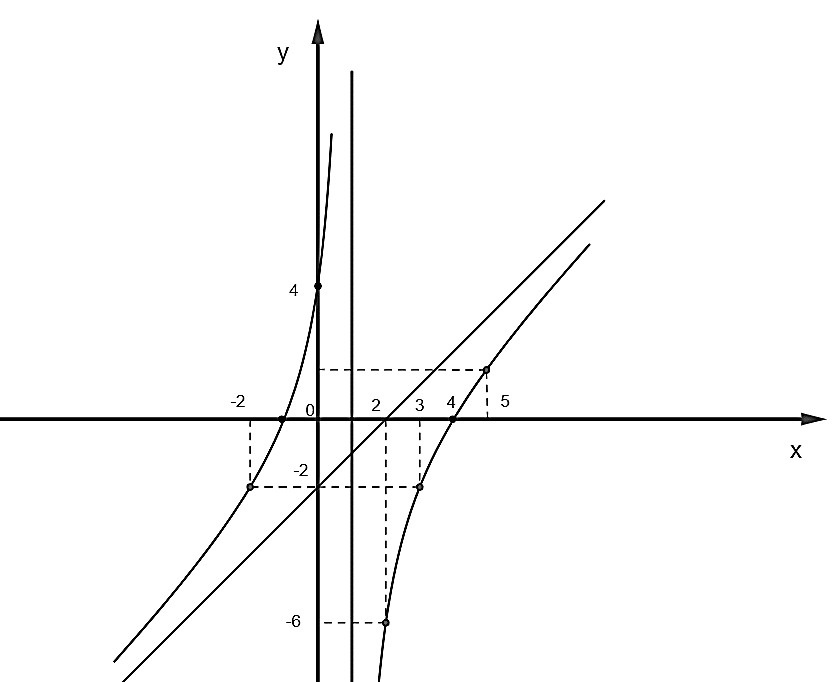
Với \(m = - 4\), ta có: \(\left( C \right):y = \frac{{{x^2} - 3x - 4}}{{x - 1}}\).
1. Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
2. Sự biến thiên
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x - 4}}{{x - 1}} = + \infty .\)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - 3x - 4}}{{x - 1}} = - \infty .\)
Do đó, đồ thị hàm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 3x - 4}}{{x - 1}} = - \infty ,\)\(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 3x - 4}}{{x - 1}} = + \infty \), do đó đồ thị hàm số nhận đường thẳng \(x = 1\) làm tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x - 4}}{{x\left( {x - 1} \right)}} = 1\), \(\mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{{x^2} - 3x - 4}}{{x - 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 2x - 4}}{{x - 1}} = - 2\).
Do đó, đồ thị hàm số nhận đường thẳng \(y = x - 2\) làm tiệm cận xiên.
Ta có: \(y' = \frac{{{x^2} - 2x + 7}}{{{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D.\)
Từ đây ta có bảng biến thiên:
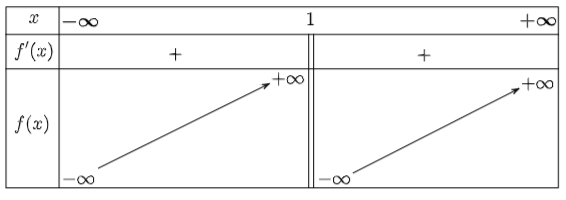
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
Hàm số không có cực trị.
3. Đồ thị
Giao điểm của đồ thị với trục tung: \(\left( {0;4} \right).\)
Giao điểm của đồ thị với trục hoành: \(\left( {4;0} \right),\left( { - 1;0} \right).\)
Đồ thị đi qua các điểm \(\left( { - 2; - 2} \right);\left( {2; - 6} \right);\left( {3; - 2} \right);\left( {5;\frac{3}{2}} \right)\).
Đồ thị nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = x - 2\) làm tiệm cận xiên.
Ta có đồ thị hàm số:
Câu 37:
Cho hàm số \(\left( C \right)\): \(y = \frac{{{x^2} - 3x + m}}{{x - 1}}.\)
Với \(m = 2\), tính giá trị lớn nhất, giá trị nhỏ nhất của \(\left( C \right)\) trên đoạn \(\left[ {2;3} \right]\).
 Xem đáp án
Xem đáp án
Với \(m = 2\), ta có: \(\left( C \right):y = \frac{{{x^2} - 3x + 2}}{{x - 1}}\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Ta có: \(y' = \frac{{{x^2} - 2x + 1}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{{\left( {x - 1} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}} = 1 > 0,\forall x \in D.\)
Do đó, hàm số đã cho đồng biến trên \(\left[ {2;3} \right]\).
Xét trên đoạn \(\left[ {2;3} \right]\), ta tính được các giá trị sau: \(y\left( 2 \right) = 0,y\left( 3 \right) = 1.\)
Vậy với \(m = 2\), giá trị lớn nhất của hàm số trên đoạn \(\left[ {2;3} \right]\) bằng \(1\) và giá trị nhỏ nhất trên đoạn \(\left[ {2;3} \right]\) bằng \(0.\)
Câu 38:
 Xem đáp án
Xem đáp án
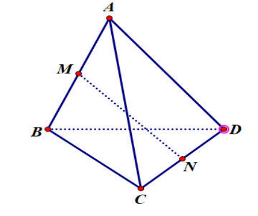
Ta có: \(\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) \Rightarrow {\left| {\overrightarrow {MN} } \right|^2} = \frac{1}{4}\left( {{{\overrightarrow {AC} }^2} + 2\overrightarrow {AC} .\overrightarrow {BD} + {{\overrightarrow {BD} }^2}} \right)\)
\( = \frac{1}{4}\left( {2{a^2} + 2\overrightarrow {AC} .\overrightarrow {BD} } \right).\)
Mà: \(\overrightarrow {AC} .\overrightarrow {BD} = \overrightarrow {AC} .\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right) = \overrightarrow {AC} .\overrightarrow {AD} - \overrightarrow {AC} .\overrightarrow {AB} \)
\( = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AD} } \right|.\cos 60^\circ - \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AB} } \right|.\cos 60^\circ = 0.\)
Suy ra \({\left| {\overrightarrow {MN} } \right|^2} = \frac{1}{4}.2{a^2} = \frac{{{a^2}}}{2}\)\( \Rightarrow \left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt 2 }}{2}.\)
Ta có: \(\overrightarrow {AC} .\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} .\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} + \overrightarrow {AC} .\overrightarrow {BD} } \right) = \frac{{{a^2}}}{2}.\)
Khi đó, \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {MN} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {MN} }}{{\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {MN} } \right|}} = \frac{{\frac{{{a^2}}}{2}}}{{a.\frac{{a\sqrt 2 }}{2}}} = \frac{{\sqrt 2 }}{2}.\)
Vậy \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {MN} } \right) = \frac{{\sqrt 2 }}{2}.\)
Câu 39:
 Xem đáp án
Xem đáp án
Gọi \(x\) là giá bán thực tế của mỗi quả bưởi Đoan Hùng \(\left( {30000 \le x \le 50000} \right)\), đơn vị: đồng.
Theo đề ta có:
Nếu bán với giá \(50000\) đồng thì bán được \(40\) quả bưởi
Giảm giá \(5000\) đồng thì bán được thêm \[50\] quả.
Giảm giá \(50000 - x\) thì bán được thêm bao nhiêu quả?
Khi đó, số quả bưởi được bán thêm là: \(\left( {50000 - x} \right)\frac{{50}}{{5000}} = \frac{1}{{100}}\left( {50000 - x} \right)\).
Do đó, số quả bưởi bán được tương ứng với giá bán \(x\):
\(40 + \frac{1}{{100}}\left( {50000 - x} \right) = \frac{{ - 1}}{{100}}x + 540\).
Gọi \(F\left( x \right)\) là hàm lợi nhuận thu được (\(F\left( x \right)\): đồng).
Ta có: \(F\left( x \right) = \left( {\frac{{ - 1}}{{100}}x + 540} \right)\left( {x - 30000} \right) = \frac{{ - 1}}{{100}}{x^2} + 840x - 16200000\).
Lúc này, bài toán trở thành tìm GTLN của hàm số:
\(F\left( x \right) = \frac{{ - 1}}{{100}}{x^2} + 840x - 16200000\) với \(30000 \le x \le 50000\).
\(F'\left( x \right) = \frac{{ - 1}}{{50}}x + 840\)
\(F'\left( x \right) = 0 \Leftrightarrow \frac{{ - 1}}{{50}}x + 840 = 0 \Leftrightarrow x = 42000\).
Vì hàm \(F\left( x \right)\) liên tục trên \(\left[ {30000;\,50000} \right]\) nên ta có:
\(F\left( {30000} \right) = 0\)
\(F\left( {42000} \right) = 1440000\)
\(F\left( {50000} \right) = 800000\).
Vậy với \(x = 42000\) thì \(F\left( x \right)\) đạt GTLN.
Vậy để cửa hàng thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi quả bưởi Đoan Hùng là \(42000\) đồng.
