Đề thi giữa kì 1 Toán 12 Cánh Diều có đáp án - Đề 05
-
405 lượt thi
-
22 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
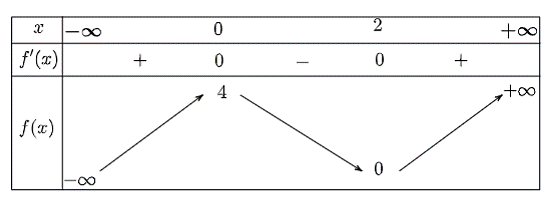
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát bảng biến thiên, ta thấy trên khoảng \[\left( {0;\,2} \right)\], \(f'\left( x \right) < 0\), do đó hàm số đã cho nghịch biến trên khoảng này.
Câu 2:
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có đồ thị như hình dưới đây.
và có đồ thị như hình dưới đây.
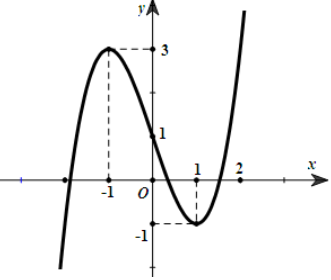
Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát đồ thị hàm số, ta thấy hàm số đã cho đạt cực tiểu tại điểm \[x = 1\] và đạt cực đại tại điểm \(x = - 1\).
Câu 3:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
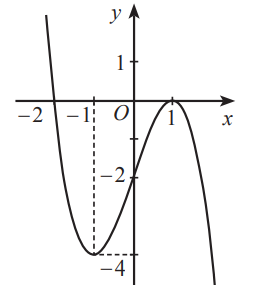
Giá trị nhỏ nhất của hàm số đã cho trên đoạn \[\left[ { - 2;\,0} \right]\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Căn cứ vào đồ thị hàm số trên, ta thấy \[\mathop {\min }\limits_{\left[ { - 2;\,0} \right]} f\left( x \right) = f\left( { - 1} \right) = - 4\].
Câu 4:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình dưới đây.
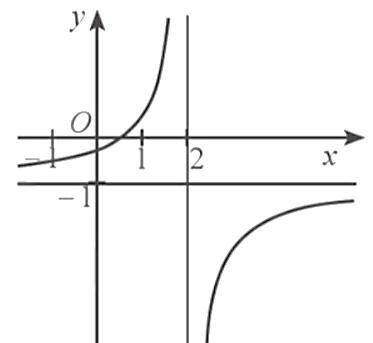
Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát hình vẽ, ta thấy:
+ Đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số đã cho.
+ Đường thẳng \(y = - 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
Câu 5:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây.
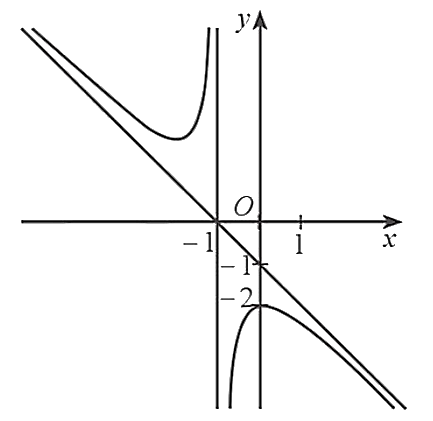
Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Từ đồ thị đã cho, ta thấy đường tiệm cận xiên của đồ thị hàm số là đường thẳng đi qua hai điểm \(\left( { - 1;0} \right)\) và \(\left( {0; - 1} \right)\). Do đó, tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng \(y = - x - 1\).
Câu 6:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây.
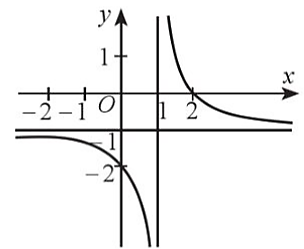
Tâm đối xứng của đồ thị hàm số có tọa độ là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đồ thị hàm số đã cho nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Giao điểm này có tọa độ là \(\left( {1;\, - 1} \right)\).
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo lý thuyết, ta có: với hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k\left( {\overrightarrow a - \overrightarrow b } \right) = k\overrightarrow a - k\overrightarrow b \).
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
+ Tập xác định của hàm số \(y = \frac{{x + 1}}{{2 - x}}\) là \(\mathbb{R}\backslash \left\{ 2 \right\}\) nên hàm số này không thể nghịch biến trên \(\mathbb{R}\).
+ Hàm số \(y = - {x^3} - 3x + 2024\) có tập xác định là \(\mathbb{R}\).
Ta có \(y' = - 3{x^2} - 3 = - 3\left( {{x^2} + 1} \right) < 0\) với mọi \(x \in \mathbb{R}\).
Do đó, hàm số này nghịch biến trên \(\mathbb{R}\). Vậy chọn đáp án B.
+ Tương tự, ta chứng minh được hai hàm số ở các phương án C và D không nghịch biến trên \(\mathbb{R}\).
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \(y' = 3\left( {x - 3} \right) \cdot {e^x} + {\left( {x - 3} \right)^2} \cdot {e^x} = {e^x} \cdot \left( {x - 3} \right) \cdot \left( {x - 1} \right)\).
Khi đó, trên khoảng \(\left( {2;\,\,4} \right)\), \(y' = 0\) khi \(x = 3\).
\(y\left( 2 \right) = {e^2};\,\,y\left( 3 \right) = 0;\,\,y\left( 4 \right) = {e^4}\).
Từ đó suy ra \(\mathop {\max }\limits_{\left[ {2;\,4} \right]} y = y\left( 4 \right) = {e^4}\).
Câu 10:
Quan sát bảng biến thiên và cho biết bảng biến thiên đó là của hàm số nào.
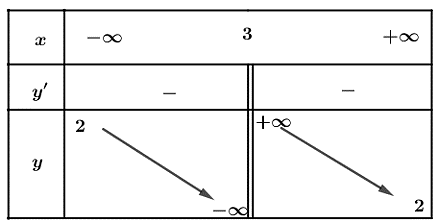
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Từ bảng biến thiên, ta thấy:
+) \(\mathop {\lim }\limits_{x \to {3^ - }} y = - \infty ;\,\,\mathop {\lim }\limits_{x \to {3^ + }} y = + \infty \), do đó đường thẳng \(x = 3\) là tiệm cận đứng của đồ thị hàm số đã cho;
+) \(\mathop {\lim }\limits_{x \to - \infty } y = 2;\,\,\mathop {\lim }\limits_{x \to + \infty } y = 2\), do đó đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số đã cho.
Trong các hàm số đã cho ở các phương án, chỉ hàm số ở phương án D thỏa mãn.
Câu 11:
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{x + d}}\) có đồ thị như hình vẽ.
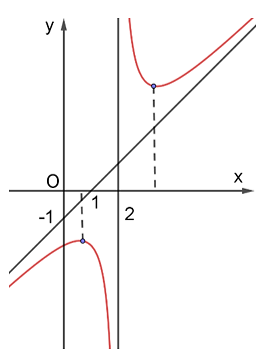
Trong các số \(a,b,c,d\) có bao nhiêu số có giá trị dương?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Do đồ thị có tiệm cận đứng là \(x = 2\) nên \(d < 0.\)
Giao điểm của đồ thị và trục tung có tung độ \(\frac{c}{d} < 0 \Rightarrow c > 0.\)
Hệ số góc của tiệm cận xiên là \(a.\) Mặt khác, từ hình vẽ hệ số góc của tiệm cận xiên là dương nên \(a > 0.\)
Lại có \(y' = \frac{{a{x^2} + 2adx + bd - c}}{{{{\left( {x + d} \right)}^2}}}\) và hai điểm cực trị của hàm số có giá trị dương.
Suy ra \({x_1}{x_2} = \frac{{bd - c}}{a} > 0 \Rightarrow bd - c > 0 \Rightarrow bd > c \Rightarrow b < 0\).
Vậy có 2 số có giá trị dương trong các số \(a,b,c,d\).
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \(ABCD\) là tứ diện đều cạnh \(a\) nên \(ABC\) là tam giác đều cạnh \(a\).
Do đó, \(\overrightarrow {AB} \cdot \overrightarrow {AC} = \left| {\overrightarrow {AB} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot \cos \left( {\overrightarrow {AB} ,\,\overrightarrow {AC} } \right)\)
\( = \left| {\overrightarrow {AB} } \right| \cdot \left| {\overrightarrow {AC} } \right| \cdot \cos \widehat {BAC}\)\( = a \cdot a \cdot \cos 60^\circ = \frac{1}{2}{a^2}\).
Câu 13:
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
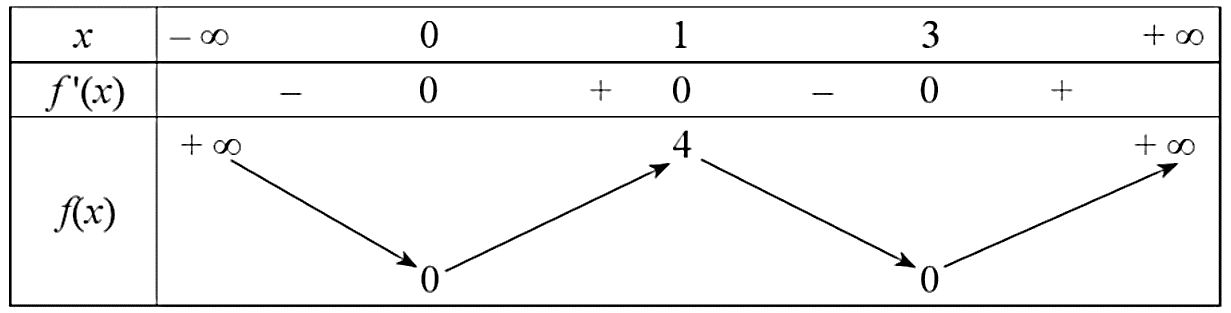
a) Hàm số \(y = f\left( x \right)\) đồng biến trên mỗi khoảng \[\left( { - \infty ;1} \right)\] và \(\left( {3;\, + \infty } \right)\).
b) Số điểm cực trị của hàm số đã cho là \(3\).
c) Hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng \(0\).
d) Đồ thị hàm số không có đường tiệm cận.
 Xem đáp án
Xem đáp án
a) S, b) Đ, c) Đ, d) Đ.
Hướng dẫn giải
– Quan sát bảng biến thiên, ta thấy hàm số đã cho đồng biến trên mỗi khoảng \[\left( {0;1} \right)\] và \(\left( {3;\, + \infty } \right)\), do đó ý a) sai.
– Ta có \(f'\left( x \right)\) đổi dấu từ “–” sang “+” tại các điểm \(x = 0\), \(x = 3\) và đổi dấu từ “+” sang “–” tại điểm \(x = 1\). Vậy hàm số \(y = f\left( x \right)\) có 3 điểm cực trị nên ý b) đúng.
– Hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng \(0\) tại \(x = 0\) và \(x = 3\) nên ý c) đúng.
– Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = + \infty \) nên đồ thị hàm số này không có đường tiệm cận. Vậy ý d) đúng.
Câu 14:
Cho hàm số \(y = {e^x} - x + 3\).
a) Hàm số đã cho nghịch biến trên \(\mathbb{R}\).
b) Hàm số đã cho đạt cực đại tại \(x = 0\).
c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ là \(\left( {0;4} \right)\).
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ.
 Xem đáp án
Xem đáp án
a) S, b) S, c) Đ, d) Đ.
Hướng dẫn giải
Xét hàm số \(y = {e^x} - x + 3\).
– Tập xác định của hàm số là \(\mathbb{R}\).
– Ta có \(y' = {e^x} - 1\); \(y' = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số như sau:
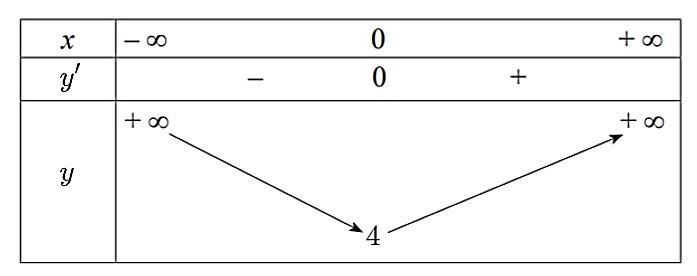
– Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\). Do đó, ý a) sai.
– Hàm số đã cho đạt cực tiểu tại \(x = 0\) và không có cực đại. Do đó, ý b) sai.
– Với \(x = 0\), ta có \(y = {e^0} - 0 + 3 = 4\) nên đồ thị hàm số cắt trục tung tại điểm \(\left( {0;4} \right)\).
Từ đó suy ra đồ thị hàm số đã cho không đi qua gốc tọa độ.
Vậy ý c) và ý d) đúng.
Câu 15:
Cho hình hộp \(ABCD.A'B'C'D'\).
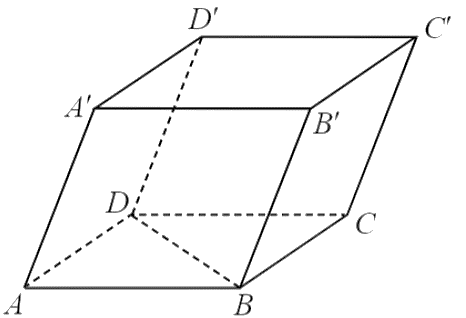
a) Các vectơ bằng với vectơ \(\overrightarrow {AD} \) là \(\overrightarrow {BC} ,\,\,\overrightarrow {B'C'} ,\,\overrightarrow {A'D'} \).
b) Các vectơ đối của vectơ \(\overrightarrow {DB} \) là \[\overrightarrow {BD} ,\,\,\overrightarrow {D'B'} \].
c) \(\overrightarrow {AB} + \overrightarrow {DC} = - 2\overrightarrow {D'C'} \).
d) \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {AC'} \).
 Xem đáp án
Xem đáp án
a) Đ, b) S, c) S, d) Đ.
Hướng dẫn giải
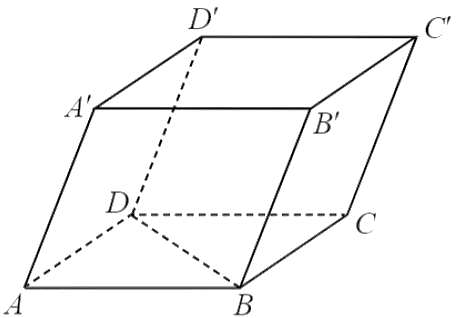
– Vì \(ABCD.A'B'C'D'\) là hình hộp nên các mặt của hình hộp này là hình bình hành.
Do đó, \(\overrightarrow {AD} = \overrightarrow {BC} = \overrightarrow {B'C'} = \overrightarrow {A'D'} \). Vậy ý a) đúng.
– Ta có \(\overrightarrow {DB} = - \overrightarrow {BD} \) và \(\overrightarrow {DB} = \overrightarrow {D'B'} = - \overrightarrow {B'D'} \).
Vậy các vectơ đối của vectơ \(\overrightarrow {DB} \) là \[\overrightarrow {BD} ,\,\,\overrightarrow {B'D'} \]. Do đó ý b) sai.
– Vì \(\overrightarrow {AB} = \overrightarrow {DC} = \overrightarrow {D'C'} \) nên \(\overrightarrow {AB} + \overrightarrow {DC} = \overrightarrow {D'C'} + \overrightarrow {D'C'} = 2\overrightarrow {D'C'} \).
Vậy ý c) sai.
– Ta có \(\overrightarrow {BB'} = \overrightarrow {AA'} ,\,\,\overrightarrow {CA} = \overrightarrow {C'A'} \). Suy ra \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {AA'} - \overrightarrow {C'A'} = \overrightarrow {AA'} + \overrightarrow {A'C'} = \overrightarrow {AC'} \).
Vậy ý d) đúng.
Câu 16:
Cho tứ diện \(ABCD\) có \(AB,\,AC,\,AD\) đôi một vuông góc và \(AB = AC = AD = 1\). Gọi \(M\) là trung điểm của \(BC\).
a) \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
b) \(\overrightarrow {AB} \cdot \overrightarrow {AD} = \overrightarrow {AC} \cdot \overrightarrow {AD} = \overrightarrow {AC} \cdot \overrightarrow {AB} = 1\).
c) \(\overrightarrow {AM} \cdot \overrightarrow {BD} = \frac{1}{2}\).
d) \(\left( {\overrightarrow {AM} ,\,\,\overrightarrow {BD} } \right) = 120^\circ \).
 Xem đáp án
Xem đáp án
a) Đ, b) S, c) S, d) Đ.
Hướng dẫn giải
– Theo quy tắc ba điểm, ta có:
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CD} \)\( = \overrightarrow {AD} + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right) = \overrightarrow {AD} + \overrightarrow {CB} \).
Vậy ý a) đúng.
– Do \(AB,\,AC,\,AD\) đôi một vuông góc nên ta có:
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = \overrightarrow {AC} \cdot \overrightarrow {AD} = \overrightarrow {AC} \cdot \overrightarrow {AB} = 0\).
Vậy ý) b sai.
– Vì \(AB = 1\) nên \({\overrightarrow {AB} ^2} = 1\).
Vì \(M\) là trung điểm của \(BC\) nên ta có:
\(\overrightarrow {AM} \cdot \overrightarrow {BD} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cdot \left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {AB} \cdot \overrightarrow {AD} - {{\overrightarrow {AB} }^2} + \overrightarrow {AC} \cdot \overrightarrow {AD} - \overrightarrow {AC} \cdot \overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( {0 - 1 + 0 - 0} \right) = - \frac{1}{2}\).
Vậy ý c) sai.
– Ta tính được \(AM = \frac{{\sqrt 2 }}{2},\,\,BD = \sqrt 2 \), suy ra
\(\cos \left( {\overrightarrow {AM} ,\,\overrightarrow {BD} } \right) = \frac{{\overrightarrow {AM} \cdot \overrightarrow {BD} }}{{\left| {\overrightarrow {AM} } \right| \cdot \left| {\overrightarrow {BD} } \right|}} = \frac{{ - \frac{1}{2}}}{{\frac{{\sqrt 2 }}{2} \cdot \sqrt 2 }} = - \frac{1}{2}\).
Vậy \(\left( {\overrightarrow {AM} ,\,\,\overrightarrow {BD} } \right) = 120^\circ \). Do đó, ý d) đúng.
Câu 17:
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Giả sử hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x - 5\) đạt cực đại tại \(x = a\) và đạt cực tiểu tại \(x = b\). Giá trị của biểu thức \(M = 2a - 3b\) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có \(f'\left( x \right) = 3{x^2} - 12x + 9\); \(f'\left( x \right) = 0 \Leftrightarrow x = 1\) hoặc \(x = 3\).
Bảng biến thiên của hàm số như sau:
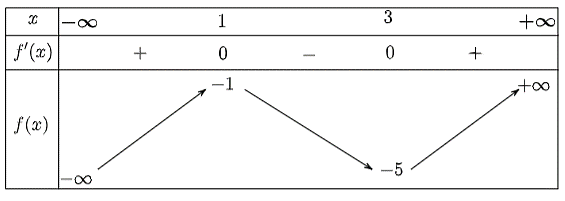
Vậy hàm số đạt cực đại tại \(x = 1\) và đạt cực tiểu tại \(x = 3\) nên suy ra \(a = 1,\,\,b = 3\).
Khi đó, \[M = 2a - 3b = 2 \cdot 1 - 3 \cdot 3 = - 7\].
Đáp số: \( - 7\).
Câu 18:
 Xem đáp án
Xem đáp án
Ta có \(y' = {e^{x + 2}} + 5 > 0\) với mọi \(x \in \mathbb{R}\).
Do đó, hàm số \(y = {e^{x + 2}} + 5x - m\) đồng biến trên \(\mathbb{R}\) nên hàm số này cũng đồng biến trên \(\left[ {0;\,\,3} \right]\). Suy ra \(\mathop {\max }\limits_{\left[ {0;\,3} \right]} y = y\left( 3 \right) = {e^{3 + 2}} + 5 \cdot 3 - m = {e^5} + 15 - m\).
Theo bài ra: \(\mathop {\max }\limits_{\left[ {0;\,3} \right]} y = y\left( 3 \right) = {e^5} \Leftrightarrow {e^5} + 15 - m = {e^5} \Leftrightarrow m = 15\).
Đáp số: \(15\).
Câu 19:
 Xem đáp án
Xem đáp án
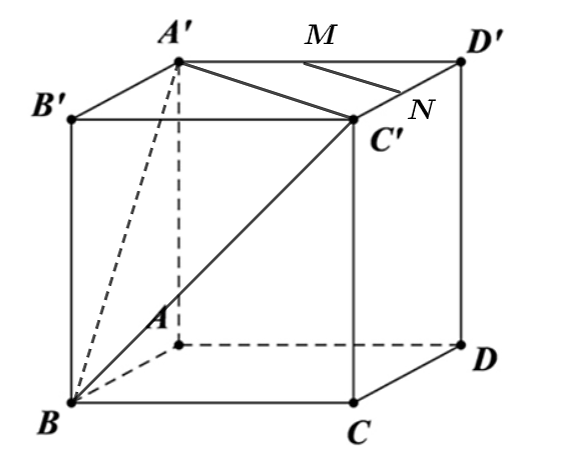
Vì \(M,N\) lần lượt là trung điểm của \(A'D'\) và \(C'D'\) nên ta suy ra \(MN\,{\rm{//}}\,A'C'\).
Do đó, \(\left( {\overrightarrow {MN} ,\,\overrightarrow {A'B} } \right) = \left( {\overrightarrow {A'C'} ,\,\overrightarrow {A'B} } \right) = \widehat {C'A'B}\).
Vì \(ABCD.A'B'C'D'\) là hình lập phương nên tam giác \(C'A'B\) là tam giác đều.
Suy ra \(\widehat {C'A'B} = 60^\circ \). Vậy \(\varphi = 60^\circ \).
Đáp số: \(60\).
Câu 20:
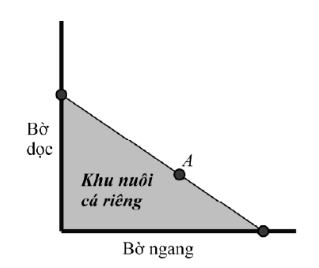
Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí \(A\). Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
 Xem đáp án
Xem đáp án
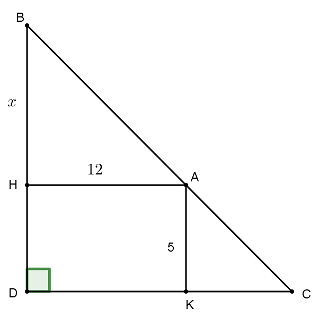
Ta mô hình hóa bài toán đã cho như hình trên với \(H,\,K\) lần lượt là hình chiếu của \(A\) lên bờ dọc \(BD\) và bờ ngang \(CD\). Khi đó, theo bài ra có \(AH = 12\,\,{\rm{m}},\,\,AK = 5\,\,{\rm{m}}\).
Suy ra \(DK = AH = 12\,\,{\rm{m}},\,\,DH = AK = 5\,\,{\rm{m}}\).
Đặt \(BH = x\,\,\,\left( {{\rm{m}},\,x > 0} \right)\).
Ta có \(AH\,{\rm{//}}\,BC,\,\,AK\,{\rm{//}}\,DH\) nên \(\frac{{BH}}{{HD}} = \frac{{BA}}{{AC}} = \frac{{DK}}{{KC}}\).
Suy ra \(KC = \frac{{HD \cdot DK}}{{BH}} = \frac{{5 \cdot 12}}{x} = \frac{{60}}{x}\) (m).
Diện tích khu nuôi cá riêng là:
\(S = \frac{1}{2}BD \cdot DC = \frac{1}{2}\left( {x + 5} \right)\left( {\frac{{60}}{x} + 12} \right) = 6x + \frac{{150}}{x} + 60\) (m2).
Xét hàm số \(S\left( x \right) = 6x + \frac{{150}}{x} + 60\) với \(x \in \left( {0; + \infty } \right)\).
Ta có \(S'\left( x \right) = 6 - \frac{{150}}{{{x^2}}} = \frac{{6{x^2} - 150}}{{{x^2}}}\). Trên khoảng \(\left( {0; + \infty } \right)\), \(S'\left( x \right) = 0 \Leftrightarrow x = 5\).
Bảng biến thiên của hàm số \(S\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) như sau:
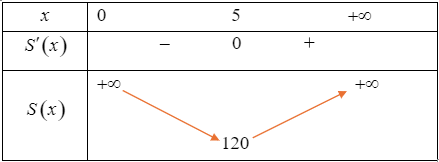
Từ bảng biến thiên, ta có \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S\left( x \right) = 120\) tại \(x = 5\).
Vậy diện tích nhỏ nhất có thể giăng dưới là \(120\) m2.
Ngoài ra, ta có thể dùng bất đẳng thức:
\[S = 6x + \frac{{150}}{x} + 60 \ge 2\sqrt {6x \cdot \frac{{150}}{x}} + 60 = 120\].
Dấu “=” xảy ra khi và chỉ khi \(6x = \frac{{150}}{x} \Leftrightarrow x = 5 \in \left( {0;\, + \infty } \right)\).
Đáp số: \(120\).
Câu 21:
 Xem đáp án
Xem đáp án
Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}\). Giả sử \(M\left( {{x_0};\,{y_0}} \right) \in \left( C \right)\), \(\left( {{x_0} \ne 1} \right)\) suy ra tiếp tuyến của \(\left( C \right)\) tại \(M\) có phương trình là \(y = \frac{{ - 1}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \frac{{2{x_0} - 1}}{{{x_0} - 1}}\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 1}}{{x - 1}} = + \infty ;\,\,\mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x - 1}}{{x - 1}} = - \infty \) nên đường thẳng \(x = 1\) là tiệm cận đứng của \(\left( C \right)\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 1}}{{x - 1}} = 2;\,\,\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 1}}{{x - 1}} = 2\) nên đường thẳng \(y = 2\) là tiệm cận ngang của \(\left( C \right)\).
Suy ra \(I\left( {1;\,\,2} \right)\).
Điểm \(A\left( {1;\,\frac{{2{x_0}}}{{{x_0} - 1}}} \right)\) là giao điểm của tiệm cận đứng và tiếp tuyến, điểm \(B\left( {2{x_0} - 1;\,2} \right)\) là giao điểm của tiệm cận ngang và tiếp tuyến.
Ta có chu vi của tam giác \(IAB\) bằng:
\(IA + IB + AB = \frac{2}{{\left| {{x_0} - 1} \right|}} + 2\left| {{x_0} - 1} \right| + \sqrt {4{{\left( {{x_0} - 1} \right)}^2} + \frac{4}{{{{\left( {{x_0} - 1} \right)}^2}}}} \).
Áp dụng bất đẳng thức AM-GM, ta có \(IA + IB + AB \ge 2\sqrt 4 + \sqrt {4 \cdot 2} = 4 + \sqrt 8 \).
Đẳng thức xảy ra khi \(\left| {{x_0} - 1} \right| = 1 \Leftrightarrow {x_0} = 0\) hoặc \({x_0} = 2\).
Vậy chu vi tam giác \(IAB\) đạt giá trị nhỏ nhất bằng \(4 + \sqrt 8 \) khi \(M\left( {0;1} \right)\) hoặc \(M\left( {2;3} \right)\).
Suy ra \(a = 4,b = 8\) nên \(a - b + 4 = 0\).
Đáp số: \(0\).
Câu 22:
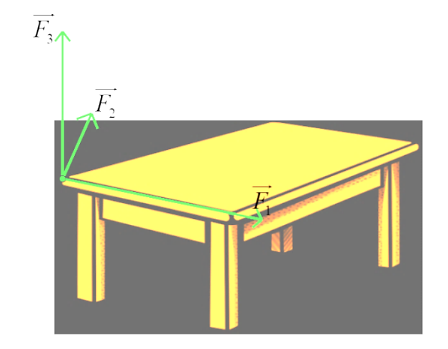
Có ba lực cùng tác động vào một cái bàn như hình vẽ dưới. Trong đó hai lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) tạo với nhau một góc \(110^\circ \) và có độ lớn lần lượt là 9 N và 4 N, lực \(\overrightarrow {{F_3}} \) vuông góc với mặt phẳng tạo bởi hai lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) và có độ lớn 7 N. Độ lớn hợp lực của ba lực trên là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị của Newton)?
 Xem đáp án
Xem đáp án
Theo đề bài, ta có hình vẽ sau:
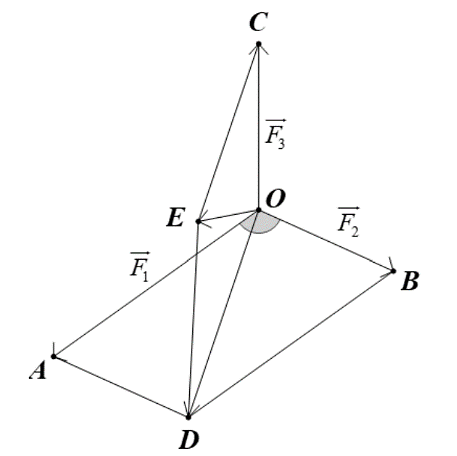
Hợp lực tác động vào ba vật là \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \).
Ta có \(\widehat {AOB} = \left( {\overrightarrow {OA} ,\,\overrightarrow {OB} } \right) = \left( {\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} } \right) = 110^\circ \). Suy ra \(\widehat {OAD} = 70^\circ \).
Áp dụng định lý côsin trong tam giác \(OAD\), ta có:
\(O{D^2} = O{A^2} + A{D^2} - 2OA \cdot AD \cdot \cos \widehat {OAD} = {9^2} + {4^2} - 2 \cdot 9 \cdot 4 \cdot \cos 70^\circ = 97 - 72\cos 70^\circ \).
Vì \(OC \bot \left( {OBDA} \right)\) nên \(OC \bot OD\). Suy ra \(ODEC\) là hình chữ nhật.
Do đó, tam giác \(OCE\) vuông tại \(C\) nên
\(O{E^2} = O{C^2} + E{C^2} = {7^2} + 97 - 72\cos 70^\circ = 146 - 72\cos 70^\circ \).
Suy ra \(OE = \sqrt {146 - 72\cos 70^\circ } \approx 11\).
Vậy độ lớn của hợp lực của ba lực đã cho bằng khoảng 11 N.
Đáp số: \(11\).
