Đề thi giữa kì 1 Toán 12 Cánh Diều có đáp án - Đề 09
-
384 lượt thi
-
40 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
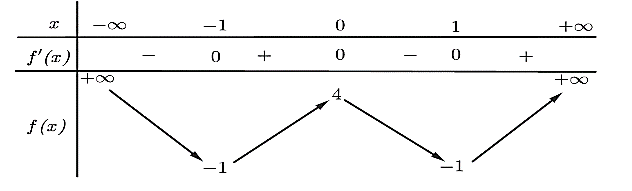
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Câu 2:
Cho hàm số \[y = f\left( x \right)\] có đồ thị hàm số như hình vẽ dưới đây.
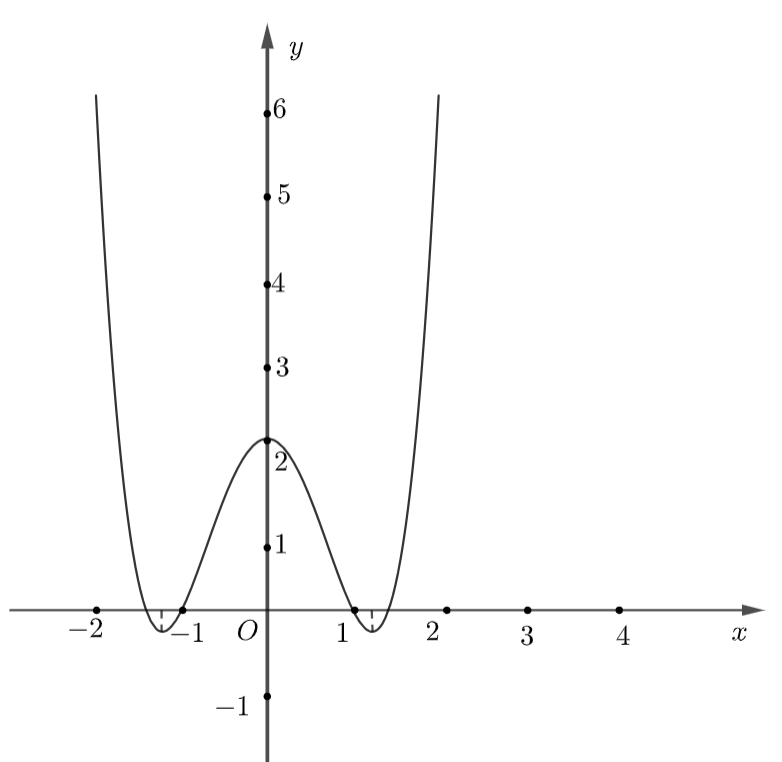
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát đồ thị hàm số, ta có:
Trên khoảng \(\left( {0;1} \right)\), đồ thị hàm số đi xuống từ trái sang phải nên hàm số đã cho nghịch biến trên khoảng này.
Vậy hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
Câu 3:
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) dưới đây:
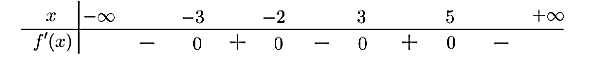
Số điểm cực trị của hàm số đã cho là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát bảng xét dấu, ta thấy hàm số có 4 điểm cực trị.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[y = {x^3}--3{x^2} + 2\] \( \Rightarrow \) \(y' = 3{x^2} - 6x\).
\(y' = 0\)\( \Leftrightarrow \)\(3{x^2} - 6x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 0\end{array} \right.\).
Ta có bảng biến thiên như sau:
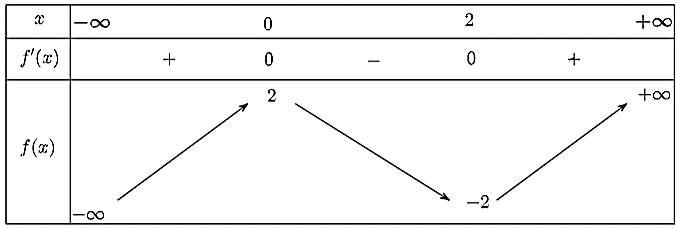
Vậy hàm số đạt cực tiểu tại \(x = 2\) và đạt cực đại tại \(x = 0\).
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(y = 3{x^4} - 6{x^2} + 1\) \( \Rightarrow y' = 12{x^3} - 12x\).
\(y' = 0 \Leftrightarrow 12{x^3} - 12x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1.\end{array} \right.\)
Ta có bảng biến thiên như sau:
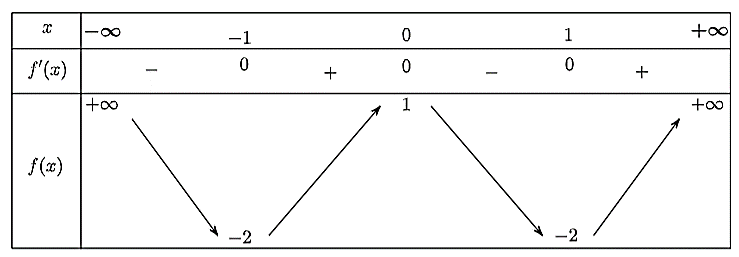
Quan sát bảng biến thiên, ta thấy:
Hàm số đạt cực đại tại \(x = 0\) và
Hàm số đạt cực tiểu tại \(x = \pm 1\) và \({y_{CT}} = - 2.\)
Câu 6:
Thể tích \(V\) (đơn vị: cm3) của 1 kg nước tại nhiệt độ \(T\left( {0^\circ C \le T \le 30^\circ C} \right)\) được tính bởi công thức sau: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\) (Nguồn: J. Stewart, Calculus, Steventh Edition, Brooks/Cole, CENGAGE Learning 2012).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0^\circ C \le T \le 30^\circ C} \right)\), giảm trong khoảng nhiệt độ gần với khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\)
\( \Rightarrow V'\left( T \right) = - 0,06426 + 0,0170086T - 2,{037.10^{ - 4}}{T^2}\)
\(V'\left( T \right) = 0 \Leftrightarrow - 2,{037.10^{ - 4}}{T^2} + 0,0170086T - 0,06426 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}T \approx 79,53\,\,\,\,(L)\\T \approx 3,97\,\,\,\,\,(TM)\end{array} \right.\).
Ta có bảng xét dấu như sau:
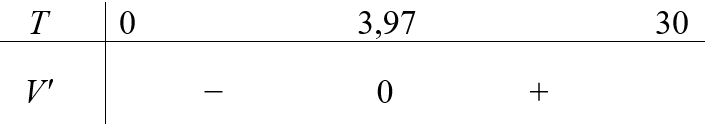
Vậy thể tích giảm khi \(T \in \left( {0^\circ C;3,97^\circ C} \right)\).
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(y = {x^3} - 3{x^2} + \left( {4 - m} \right)x\); \(y' = 3{x^2} - 6x + 4 - m\).
Để thỏa mãn yêu cầu bài toán thì \(y' \ge 0,\forall x \in \left( {2; + \infty } \right)\).
\( \Leftrightarrow 3{x^2} - 6x + 4 - m \ge 0,\forall x \in \left( {2; + \infty } \right).\)
\( \Leftrightarrow m \le 3{x^2} - 6x + 4,\forall x \in \left( {2; + \infty } \right).\)
\( \Leftrightarrow m \le \mathop {\min }\limits_{\left( {2; + \infty } \right)} g(x)\) với \(g(x) = 3{x^2} - 6x + 4.\)
Ta có: \(g'\left( x \right) = 6x - 6\)
\(g'\left( x \right) = 0 \Leftrightarrow 6x - 6 = 0 \Leftrightarrow x = 1\).
Ta có bảng biến thiên:
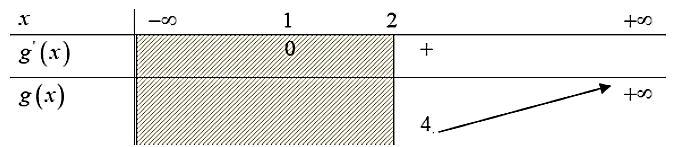
Dựa vào bảng biến thiên, suy ra \(m \le 4\) thỏa mãn yêu cầu bài toán.
Vậy \(m \in \left( { - \infty ;4} \right]\) thì hàm số đã cho đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Câu 8:
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \(\left[ { - 2;3} \right]\) có đồ thị như hình vẽ dưới đây:
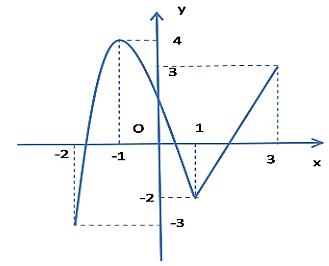
Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;3} \right]\). Giá trị của \(2m - 3M\) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Quan sát đồ thị hàm số, ta có:
Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ { - 2;3} \right]\) là \(M = 4\) khi \(x = - 1\).
Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ { - 2;3} \right]\) là \(m = - 3\) khi \(x = - 2\).
Suy ra: \(2m - 3M\)= \(2.\left( { - 3} \right) - 3.4\) = \( - 18\).
Câu 9:
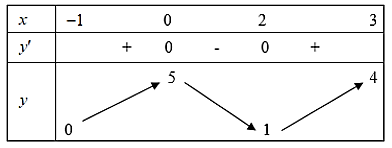
Cho hàm số \[y = f\left( x \right)\] liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;3} \right]\) như hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát bảng biến thiên, ta thấy:
Xét trên đoạn \(\left[ { - 1;3} \right]\), giá trị lớn nhất của hàm số là \(f\left( 0 \right) = 5\).
Vậy \(\mathop {\max }\limits_{[ - 1;3]} \)\[f\left( x \right) = f\left( 0 \right)\].
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tập xác định: \(D = \left[ {1; + \infty } \right)\).
Ta có: \(y' = 1 - \frac{1}{{2\sqrt {x - 1} }} = \frac{{2\sqrt {x - 1} - 1}}{{2\sqrt {x - 1} }}\).
\(y' = 0 \Leftrightarrow \frac{{2\sqrt {x - 1} - 1}}{{2\sqrt {x - 1} }} = 0\)\( \Leftrightarrow 2\sqrt {x - 1} = 1 \Leftrightarrow x = \frac{5}{4}\).
Ta có bảng biến thiên như sau:
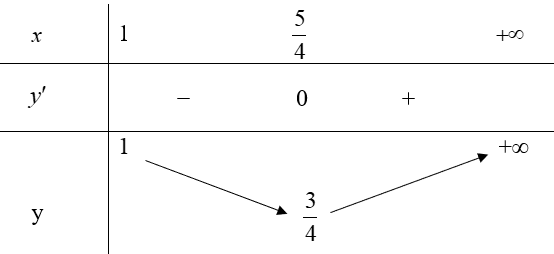
Từ bảng biến thiên ta thấy:
Hàm số có giá trị nhỏ nhất là \(\frac{3}{4}\) và không có giá trị lớn nhất.
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[y = \;\frac{{2{x^2} + 3x + 3}}{{x + 1}}\] \( \Rightarrow y' = \frac{{2{x^2} + 4x}}{{{{\left( {x + 1} \right)}^2}}}\).
\(y' = 0 \Leftrightarrow \frac{{2{x^2} + 4x}}{{{{\left( {x + 1} \right)}^2}}} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ {0;2} \right]\\x = - 2 \notin \left[ {0;2} \right]\end{array} \right.\).
Xét trên đoạn \(\left[ {0;2} \right]\), ta tính được các giá trị \(y\left( 0 \right) = 3,y\left( 2 \right) = \frac{{17}}{3}\).
Vậy \(M = \frac{{17}}{3},m = 3.\)
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(y = \frac{{x + {m^2}}}{{x - 1}}\)\( \Rightarrow y' = \frac{{ - 1 - {m^2}}}{{{{\left( {x - 1} \right)}^2}}}\).
Vì \( - 1 - {m^2} < 0\,\,\forall m \in \mathbb{R} \Rightarrow \frac{{ - 1 - {m^2}}}{{{{\left( {x - 1} \right)}^2}}} < 0,\,\,\,\forall x \in \left[ {2;3} \right]\).
Suy ra \(\mathop {\min }\limits_{\left[ {2;3} \right]} y = y\left( 3 \right) = 14\).
Ta có: \(y\left( 3 \right) = \frac{{3 + {m^2}}}{{3 - 1}} = 14\)\( \Rightarrow {m^2} = 25\) \( \Leftrightarrow m = \pm 5\).
Mà theo đề bài, \(m\) nhận giá trị nguyên dương nên \(m = 5.\)
Vậy có 1 giá trị nguyên dương của tham số \(m\) thỏa mãn.
Câu 13:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ:
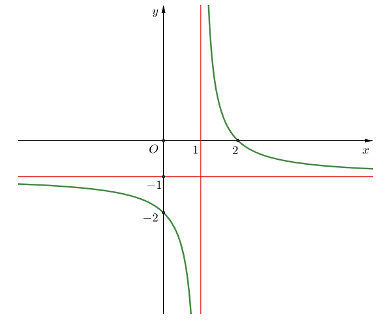
Đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát đồ thị hàm số, ta có:
Đường thẳng \(x = 1\) là đường tiệm cận đứng của đồ thị hàm số.
Câu 14:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ.
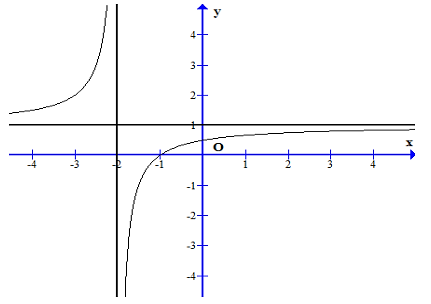
Phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát đồ thị hàm số, ta có:
Đường thẳng \(x = - 2\) là đường tiệm cận đứng của đồ thị hàm số.
Đường thẳng \(y = 1\) là đường tiệm cận ngang của đồ thị hàm số.
Vậy tiệm cận đứng \(x = - 2\), tiệm cận ngang \(y = 1\).
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét các đáp án A, B, C, D ta lấy tử số chia mẫu số. Ta có:
Đáp án A, ta có:
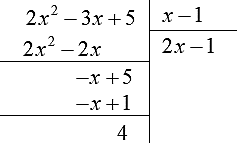
Vậy đường thẳng \(y = 2x - 1\) là đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x + 5}}{{x - 1}}\).
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có điều kiện xác định: \(D = \left[ { - 4; + \infty } \right)\backslash \left\{ {0; - 1} \right\}.\)
Xét: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = 0\).
Do đó, đường thẳng \(y = 0\) là đường tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = + \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = - \infty .\)
Do đó, \(x = - 1\) là đường tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{{x\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \frac{1}{4}\).
\(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{x}{{x\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \frac{1}{4}\).
Do đó, \(x = 0\) không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 2}}{{x + 2}} = 1.\)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 2}}{{x + 2}} = 1.\)
Do đó, \(y = 1\) là đường tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - {2^ - }} y = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{x - 2}}{{x + 2}} = + \infty .\)
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{x - 2}}{{x + 2}} = - \infty .\)
Do đó, \(x = - 2\) là đường tiệm cận đứng của đồ thị hàm số.
Vậy tọa độ giao điểm \(I\) của hai đường tiệm cận của đồ thị \[\left( C \right)\] là \(I\left( { - 2;1} \right)\).
Câu 18:
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\).
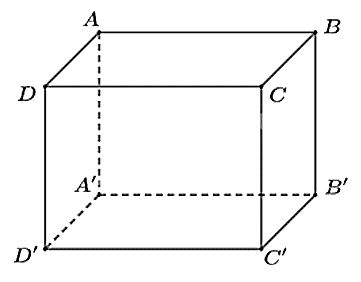
Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên
\(\overrightarrow {AB} = \overrightarrow {A'B'} = \overrightarrow {D'C'} = \overrightarrow {DC} \) và \(\overrightarrow {AD} = \overrightarrow {A'D'} = \overrightarrow {B'C'} = \overrightarrow {BC} \).
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
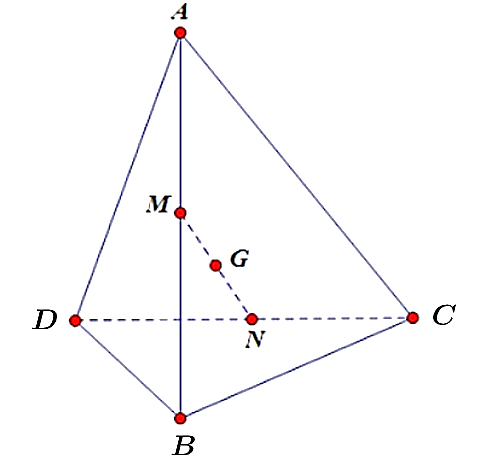
Có \(M,N,G\) lần lượt là trung điểm \(AB,CD,MN\). Theo quy tắc trung điểm, ta có:
\(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} \); \(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \); \(\overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \).
Suy ra \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \) hay \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {DG} \).
Với \(O\) là điểm bất kì, ta có:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OG} + \overrightarrow {GA} + \overrightarrow {OG} + \overrightarrow {GB} + \overrightarrow {OG} + \overrightarrow {GC} + \overrightarrow {OG} + \overrightarrow {GD} \)
\( = 4\overrightarrow {OG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \)\( = 4\overrightarrow {OG} \).
Vậy đáp án A sai và các đáp án B, C, D đúng.
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo đề bài, \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ đều khác vectơ \(\overrightarrow 0 \). Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)\)
\( = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \)
\( = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos 60^\circ - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos 60^\circ \)
\( = 0\).
Suy ra \(\left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = 90^\circ \).
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
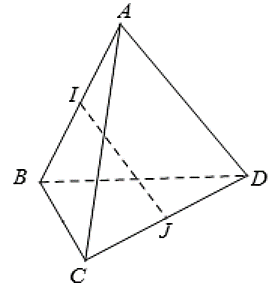
Ta có: \(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right)\).
Vì tam giác \(ABC\) có \(AB = AC\) và \(\widehat {BAC} = 60^\circ \) nên tam giác \(ABC\) đều.
Suy ra \(CI \bot AB\).
Tương tự ta có tam giác \(ABD\) đều nên \(DI \bot AB\).
Xét: \(\overrightarrow {IJ} .\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right).\overrightarrow {AB} = \frac{1}{2}\overrightarrow {IC} .\overrightarrow {AB} + \frac{1}{2}\overrightarrow {ID} .\overrightarrow {AB} \) \( = \overrightarrow 0 \).
Suy ra \(\left( {\overrightarrow {IJ} ,\overrightarrow {AB} } \right) = 90^\circ \).
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
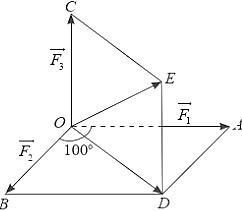
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) là ba lực tác động vào vật tại điểm \(O\) lần lượt có độ lớn \(25N,12N,4N\).
Vẽ \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Dựng hình bình hành \(OADB\) và hình bình hành \(ODEC\).
Hợp lực tác động vào vật là:
\(\overrightarrow F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} .\)
Áp dụng định lí côsin trong tam giác \(OBD\), ta có:
\(O{D^2} = B{D^2} + O{B^2} - 2.BD.OB.\cos \widehat {OBD} = O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \)
Vì \(OC \bot \left( {OADB} \right)\) nên \(OC \bot OD\), suy ra \(ODEC\) là hình chữ nhật.
Do đó, tam giác \(DOE\) vuông tại \(D\).
Ta có: \(O{E^2} = O{C^2} + O{D^2} = O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \).
Suy ra:
\(OE = \sqrt {O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ } \)\( = \sqrt {{4^2} + {{25}^2} + {{12}^2} + 2.25.12.\cos 100^\circ } \)
\(OE \approx 26N\).
Vậy độ lớn của hợp lực \(F = OE \approx 26N\).
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trong không gian với hệ trục \[Oxyz\], có \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \) nên tọa độ \(\overrightarrow a = \left( { - 1;2; - 3} \right)\).
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Trong không gian \[Oxyz\], hình chiếu vuông góc của điểm \(A\left( {3;5;2} \right)\) trên trục \(Ox\) có tọa độ \(\left( {3;0;0} \right)\).
Câu 26:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có điểm đối xứng của \(A\left( {1;2; - 3} \right)\) qua mặt phẳng \[\left( {Oyz} \right)\] ta được điểm có tọa độ \(\left( { - 1;2; - 3} \right)\).
Câu 27:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi \(C\left( {x;y;z} \right)\), ta có: \(\overrightarrow {DC} = \overrightarrow {AB} \).
Suy ra: \(\left\{ \begin{array}{l}x - 0 = 0 - \left( { - 3} \right)\\y - 0 = 2 - 0\\z - 1 = 0 - 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\\z = 1\end{array} \right.\). Vậy \(C\left( {3;2;1} \right)\).
Gọi \(C'\left( {{x_0};{y_0};{z_0}} \right)\), ta có: \(\overrightarrow {CC'} = \overrightarrow {AA'} \).
Suy ra \(\left\{ \begin{array}{l}{x_0} - 3 = 1 - \left( { - 3} \right)\\{y_0} - 2 = 2 - 0\\{z_0} - 1 = 3 - 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 7\\{y_0} = 4\\{z_0} = 4\end{array} \right.\). Vậy \(C'\left( {7;4;4} \right)\).
Câu 28:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(\overrightarrow {AB} = \left( { - 5; - 4; - 1} \right)\) \( \Rightarrow AB = \sqrt {{{\left( { - 5} \right)}^2} + {{\left( { - 4} \right)}^2} + {{\left( { - 1} \right)}^2}} = \sqrt {42} .\)
\(\overrightarrow {AC} = \left( {3;1;2} \right)\) \( \Rightarrow AC = \sqrt {{3^2} + {1^2} + {2^2}} = \sqrt {14} \).
Ta có: \(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{ - 5.3 + \left( { - 4} \right).1 + \left( { - 1} \right).2}}{{\sqrt {42} .\sqrt {14} }} = - \frac{{\sqrt 3 }}{2}\).
Suy ra \(\widehat {BAC} = 150^\circ \).
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi điểm \(M\) thuộc trục \(Ox\) có tọa độ \(\left( {x;0;0} \right)\).
Theo đề, ta có \(M\) cách đều hai điểm \(A\left( {4;2; - 1} \right)\) và \(B\left( {2;1;0} \right)\) hay \(MA = MB\).
Ta có: \(MA = MB\) \( \Rightarrow \)\(M{A^2} = M{B^2}\)
\( \Leftrightarrow {\left( {x - 4} \right)^2} + {(0 - 2)^2} + {\left[ {0 - \left( { - 1} \right)} \right]^2} = {\left( {2 - x} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( {0 - 0} \right)^2}\)
\( \Leftrightarrow {x^2} - 8x + 16 + 4 + 1 = {x^2} - 4x + 4 + 1\)
\( \Leftrightarrow 4x = 16\)
\( \Leftrightarrow x = 4.\)
Vậy \(M\left( {4;0;0} \right)\).
Câu 30:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi \(I\left( {x;y;z} \right)\) là điểm thỏa mãn \(\overrightarrow {IA} = 2\overrightarrow {IB} \) \( \Leftrightarrow \left\{ \begin{array}{l}1 - x = 2\left( {2 - x} \right)\\2 - y = 2\left( { - 1 - y} \right)\\1 - z = 2\left( {3 - z} \right).\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 4\\z = 5\end{array} \right. \Rightarrow I\left( {3; - 4;5} \right)\).
Khi đó, ta có: \(M{A^2} - 2M{B^2} = {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} - 2{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} = - M{I^2} + 2\overrightarrow {MI} .\left( {\overrightarrow {IA} - 2\overrightarrow {IB} } \right) + I{A^2} - 2I{B^2}\)
\( = - M{I^2} + I{A^2} - 2I{B^2}\).
Để \[M{A^2}--2M{B^2}\] lớn nhất thì \( - M{I^2} + I{A^2} - 2I{B^2}\) lớn nhất \( \Leftrightarrow MI\) nhỏ nhất \( \Leftrightarrow M\) là hình chiếu của \(I\) trên mặt phẳng \(\left( {Oxy} \right)\).
Suy ra \(M\left( {3; - 4;0} \right)\).
Câu 31:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(3\overrightarrow v = \left( { - 3; - 6;3} \right)\).
Do đó, \(\overrightarrow u + 3\overrightarrow v = \left( { - 2; - 10;3} \right)\).
Câu 32:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{ - 1.0 + 1.\left( { - 1} \right) + 0.0}}{{\sqrt {{{\left( { - 1} \right)}^2} + {1^2} + {0^2}} .\sqrt {{0^2} + {{\left( { - 1} \right)}^2} + {0^2}} }}\)\( = \frac{{ - 1}}{{\sqrt 2 .1}} = - \frac{1}{{\sqrt 2 }}\).
Suy ra \(\left( {\overrightarrow u ,\overrightarrow v } \right) = 135^\circ \).
Câu 33:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{2.1 + 1.3 + \left( { - 1} \right).m}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {3^2} + {m^2}} }}\).
Vì \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \) nên \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 0\).
Suy ra \(2.1 + 1.3 + \left( { - 1} \right).m = 0\) hay \(m = 5\).
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi \(G(x;y;z)\) là trọng tâm của tam giác \(ABC\).
Ta có: \(\left\{ \begin{array}{l}x = \frac{{1 + \left( { - 1} \right) + 0}}{3} = 0\\y = \frac{{ - 2 + 2 + 0}}{3} = 0\\z = \frac{{3 + 5 + 1}}{3} = 3\end{array} \right.\)\( \Rightarrow G\left( {0;0;3} \right)\).
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi \(E\left( {x;y;z} \right)\), ta có: \(\overrightarrow {CE} = 2\overrightarrow {EB} \).
\( \Leftrightarrow \left\{ \begin{array}{l}x - 7 = 2\left( {1 - x} \right)\\y - 4 = 2\left( {2 - y} \right)\\z + 2 = 2\left( { - 3 - z} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = \frac{8}{3}\\z = \frac{{ - 8}}{3}\end{array} \right.\)\( \Rightarrow E\left( {3;\frac{8}{3}; - \frac{8}{3}} \right)\).
Câu 36:
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( { - 2;1;2} \right)\), \(\overrightarrow b = \left( {1;1; - 1} \right)\).
Xác định tọa độ của \(\overrightarrow u = \overrightarrow a - 2\overrightarrow b \). (0,25 điểm)
 Xem đáp án
Xem đáp án
Ta có: \(2\overrightarrow b = \left( {2;2; - 2} \right)\).
Do đó, \(\overrightarrow a - 2\overrightarrow b = \left( { - 2 - 2;1 - 2;2 - \left( { - 2} \right)} \right) = \left( { - 4; - 1;4} \right)\).
Vậy \(\overrightarrow u = \left( { - 4; - 1;4} \right)\).
Câu 37:
 Xem đáp án
Xem đáp án
Ta có: \(\left| {\overrightarrow u } \right| = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 1} \right)}^2} + {4^2}} = \sqrt {33} \).
Vậy độ dài vectơ \(\overrightarrow u \) là \(\sqrt {33} \).
Câu 38:
Trong không gian \[Oxyz\], cho hai vectơ \(\overrightarrow a = \left( { - 2;1;2} \right)\), \(\overrightarrow b = \left( {1;1; - 1} \right)\).
Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). (0,5 điểm)
 Xem đáp án
Xem đáp án
Ta có: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 2.1 + 1.1 + 2.\left( { - 1} \right)}}{{\sqrt {{{\left( { - 2} \right)}^2} + {1^2} + {2^2}} .\sqrt {{1^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{ - \sqrt 3 }}{3}\).
Vậy \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{ - \sqrt 3 }}{3}\).
Câu 39:
Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các suối nước đổ về hồ. Từ lúc 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian \(t\) (giờ) trong ngày cho bởi công thức:
\(h(t) = - \frac{1}{3}{t^3} + 5{t^2} + 24t\), \(\left( {t > 0} \right)\).
Biết rằng phải thông báo cho các hộ dân phải di dời đi trước khi xả nước theo quy định trước 5 giờ. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước mấy giờ? Biết rằng mực nước trong hồ phải đi lên cao nhất mới xả nước. (1,0 điểm)
 Xem đáp án
Xem đáp án
Xét: \(h(t) = - \frac{1}{3}{t^3} + 5{t^2} + 24t\), \(\left( {t > 0} \right).\)
Ta có: \(h'(t) = - {t^2} + 10t + 24\)
\(h'(t) = 0 \Leftrightarrow - {t^2} + 10t + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 12 \in \left( {0; + \infty } \right)\\t = - 2 \notin \left( {0; + \infty } \right)\end{array} \right.\)
Bảng biến thiên:
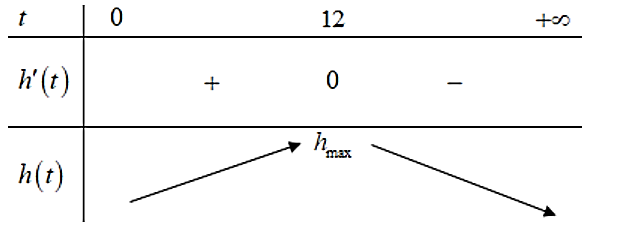
Để mực nước lên cao nhất thì phải mất 12 giờ.
Vậy phải thông báo cho dân dời đi vào 15 giờ chiều cùng ngày.
Câu 40:
 Xem đáp án
Xem đáp án
Đồ thị \(\left( H \right)\) có tiệm cận đứng là đường thẳng \({\Delta _1}:x = - 1\) và tiệm cận ngang là đường thẳng \({\Delta _2}:y = 4\).
Gọi \(M\left( {{x_0};\frac{{4{x_0} - 5}}{{{x_0} + 1}}} \right) \in \left( H \right)\), \({x_0} \ne - 1,{x_0} < 0\).
Khi đó, ta có: \({d_1} = d\left( {M,{\Delta _1}} \right) = \left| {{x_0} + 1} \right|\) và \({d_2} = d\left( {M,{\Delta _2}} \right) = \frac{9}{{\left| {{x_0} + 1} \right|}}.\)
\( \Rightarrow {d_1}.{d_2} = \left| {{x_0} + 1} \right|.\frac{9}{{\left| {{x_0} + 1} \right|}} = 9\).
Ta có: \({d_1} + {d_2} \ge 2\sqrt {{d_1}{d_2}} = 6\) nên \(\min \left( {{d_1} + {d_2}} \right) = 6\) khi \({d_1} = {d_2} \Leftrightarrow \left| {{x_0} + 1} \right| = \frac{9}{{\left| {{x_0} + 1} \right|}}.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = - 4\end{array} \right.\)
Do \({x_0} < 0\) nên chọn \({x_0} = - 4\), khi đó \(M\left( { - 4;7} \right) \Rightarrow S = 9.\)
