 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Ta có điều kiện xác định: \(D = \left[ { - 4; + \infty } \right)\backslash \left\{ {0; - 1} \right\}.\)
Xét: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = 0\).
Do đó, đường thẳng \(y = 0\) là đường tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = + \infty .\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = - \infty .\)
Do đó, \(x = - 1\) là đường tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{{x\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \frac{1}{4}\).
\(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{x}{{x\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{\left( {x + 1} \right)\left( {\sqrt {x + 4} + 2} \right)}} = \frac{1}{4}\).
Do đó, \(x = 0\) không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các suối nước đổ về hồ. Từ lúc 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian \(t\) (giờ) trong ngày cho bởi công thức:
\(h(t) = - \frac{1}{3}{t^3} + 5{t^2} + 24t\), \(\left( {t > 0} \right)\).
Biết rằng phải thông báo cho các hộ dân phải di dời đi trước khi xả nước theo quy định trước 5 giờ. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước mấy giờ? Biết rằng mực nước trong hồ phải đi lên cao nhất mới xả nước. (1,0 điểm)
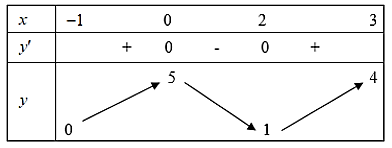
Cho hàm số \[y = f\left( x \right)\] liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;3} \right]\) như hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
Thể tích \(V\) (đơn vị: cm3) của 1 kg nước tại nhiệt độ \(T\left( {0^\circ C \le T \le 30^\circ C} \right)\) được tính bởi công thức sau: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\) (Nguồn: J. Stewart, Calculus, Steventh Edition, Brooks/Cole, CENGAGE Learning 2012).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0^\circ C \le T \le 30^\circ C} \right)\), giảm trong khoảng nhiệt độ gần với khoảng nào sau đây?
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \(\left[ { - 2;3} \right]\) có đồ thị như hình vẽ dưới đây:
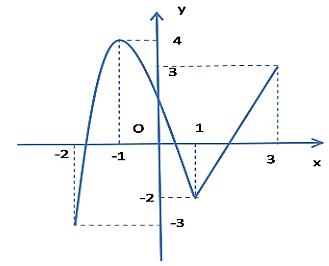
Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;3} \right]\). Giá trị của \(2m - 3M\) bằng: