Trong không gian \[Oxyz\], cho điểm \[H\left( {1;2; - 2} \right)\]. Mặt phẳng \[\left( \alpha \right)\] đi qua \[H\] và cắt các trục \[Ox,Oy,Oz\] tại \[A,B,C\] sao cho \[H\] là trực tâm của tam giác \[ABC\]. Viết phương trình mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng \[\left( \alpha \right)\].
A. \[{x^2} + {y^2} + {z^2} = 81.\]
B. \[{x^2} + {y^2} + {z^2} = 1.\]
C. \[{x^2} + {y^2} + {z^2} = 9.\]
D. \[{x^2} + {y^2} + {z^2} = 25.\]
Giải bởi Vietjack
Đáp án đúng là: C
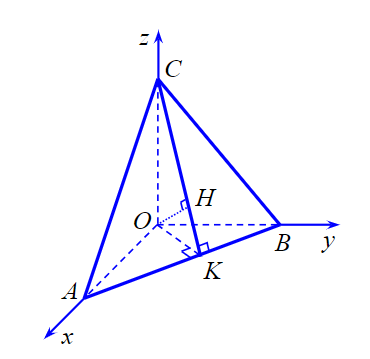
Ta có
\[H\] là trực tâm của tam giác \[ABC\], suy ra \[OH \bot \left( {ABC} \right)\].
Thật vậy:
\[\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\end{array} \right. \Rightarrow OC \bot AB\] (1)
Mà \[CH \bot AB\] (vì \[H\] là trực tâm tam giác \[ABC\]) (2).
Từ (1) và (2) suy ra \[AB \bot \left( {OHC} \right)\]\[ \Rightarrow AB \bot OH\].
Tương tự, ta suy ra \[BC \bot \left( {OAH} \right)\]\[ \Rightarrow BC \bot OH.\]
Từ đây suy ra \[OH \bot \left( {ABC} \right).\]
Khi đó, mặt cầu tâm \[O\] tiếp xúc mặt phẳng \[\left( {ABC} \right)\] có bán kính \[R = OH = 3.\]
Vậy mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng \[\left( \alpha \right)\] là \[{x^2} + {y^2} + {z^2} = 9.\]
Có tất cả bao nhiêu giá trị nguyên của \[m\] để phương trình \[{x^2} + {y^2} + {z^2} + 4mx + 2my - 2mz + 9{m^2} - 28 = 0\] là phương trình mặt cầu?
Trong không gian với hệ trục tọa độ \[Oxyz\], cho mặt cầu có phương trình \[\left( S \right):\]\[{\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 3} \right)^2} = 16\] có tâm là
II. Thông hiểu
Trong không gian với hệ trục tọa độ \[Oxyz\], cho mặt cầu \[\left( S \right):\] \[{x^2} + {y^2} + {z^2} - 4x - 2y + 2z - 3 = 0\] và một điểm \[M\left( {4;2; - 2} \right)\]. Mệnh đề nào sau đây là đúng?
Cho mặt phẳng \[\left( P \right):2x + 2y + z - {m^2} + 4m - 5 = 0\] và mặt cầu có phương trình \[\left( S \right):\]\[{x^2} + {y^2} + {z^2} - 2x + 2y - 2z - 6 = 0\]. Giá trị của \[m\] để \[\left( P \right)\] tiếp xúc với \[\left( S \right)\] là
Cho điểm \[M\] nằm ngoài mặt cầu \[S\left( {O;R} \right)\]. Khẳng định nào sau đây là đúng?
III. Vận dụng
Trong không gian \[Oxyz\], mặt cầu (S) đi qua điểm \[O\] và cắt các tia \[Ox,\]\[Oy,\]\[Oz\] lần lượt tại các điểm \[A,B,C\] khác \[O\] thỏa mãn tam giác \[ABC\] có trọng tâm là điểm \[G\left( { - 6; - 12;18} \right)\]. Tọa độ tâm của mặt cầu (S) là
Trong không gian \[Oxyz\], cho mặt cầu có phương trình \[\left( S \right):\]\[{x^2} + {y^2} + {z^2}\]\[ + 2x - 4y - 6z + m - 3 = 0\]. Tìm số thực của tham số \[m\] để mặt phẳng \[\left( \beta \right):\]\[2x - y + 2z - 8 = 0\] cắt \[\left( S \right)\] theo một đường tròn có chu vi bằng \[8\pi .\]
I. Nhận biết
Trong không gian \[Oxyz\], mặt cầu tâm \[I\left( {{x_0};{y_0};{z_0}} \right)\] bán kính \[R\] có phương trình là:
Trong không gian với hệ trục tọa độ \[Oxyz\], phương trình nào sau đây là phương trình mặt cầu
Điều kiện đề phương trình \[{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\] là phương trình mặt cầu là
Phương trình mặt cầu tâm \[I\left( {1; - 2;3} \right)\] bán kính \[R = 3\] là
Xác định tâm và bán kính mặt cầu \[{x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\] ta được
Trong các phương trình sau, phương trình nào là phương trình mặt cầu?
Trong không gian \[Oxyz\], cho điểm \[I\left( {3;4;2} \right)\]. Phương trình mặt cầu tâm \[I\] tiếp xúc với trục \[Oz\] là
Trong không gian \[Oxyz\], cho mặt cầu \[{x^2} + {y^2} + z{}^2 - 4x + 1 = 0\] có tâm và bán kính là
