Tiệm cận đứng của đồ thị hàm số \(y = \frac{x}{{{x^2} - 4x}}\) là
A. \(x = 0.\)
B. \(x = - 4.\)
C. \(x = 0\); \(x = 4.\)
D. \(x = 4.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{{x\left( {x - 4} \right)}} = - \frac{1}{4}\); \(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \frac{x}{{x\left( {x - 4} \right)}} = - \frac{1}{4}\).
Do đó x = 0 không là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {4^ + }} y = \mathop {\lim }\limits_{x \to {4^ + }} \frac{x}{{x\left( {x - 4} \right)}} = + \infty \); \(\mathop {\lim }\limits_{x \to {4^ - }} y = \mathop {\lim }\limits_{x \to {4^ - }} \frac{x}{{x\left( {x - 4} \right)}} = - \infty \).
Do đó x = 4 là tiệm cận đứng của đồ thị hàm số.
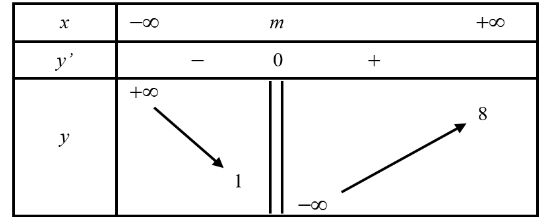
Cho đồ thị hàm số y = f(x) có bảng biến thiên xác định như hình. Biết rằng đồ thị hàm số có tiệm cận đứng x = x0, tiệm cận ngang y = y0 và x0y0 = 16. Tìm m.
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x + 3}}{{x + 1}}\) là
Cho hàm số y = f(x) có đồ thị như hình vẽ
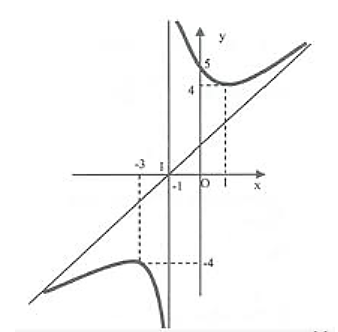
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) có bảng biến thiên như hình bên.
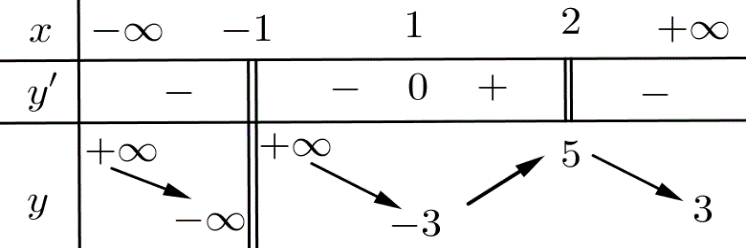
Số tiệm cận của đồ thị hàm số đã cho là.
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 3}}\) có một đường tiệm cận ngang là
Cho hàm số y = f(x) có bảng biến thiên
![Cho hàm số y = f(x) có bảng biến thiên Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để đồ thị hàm số có 4 tiệm cận. (ảnh 1)](https://video.vietjack.com/upload2/images/1728876922/1728877622-image6.png)
Có bao nhiêu giá trị nguyên của m ∈ [−4; 4] để đồ thị hàm số có 4 tiệm cận.
I. Nhận biết
Cho hàm số y = f(x) có đồ thị như hình vẽ
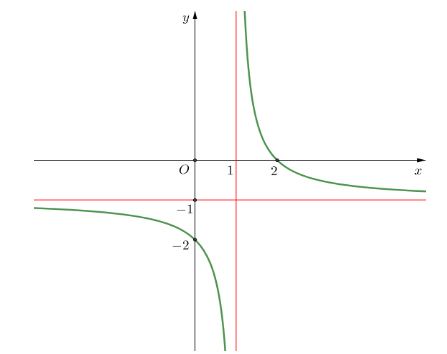
Đồ thị hàm số đã cho có tiệm cận đứng bằng
II. Thông hiểu
Đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 3}}\) có bao nhiêu đường tiệm cận?
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
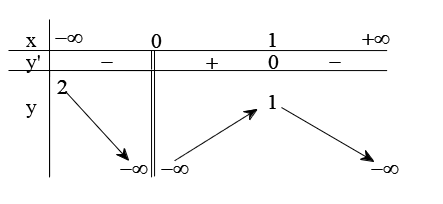
Tổng số đường tiệm cận của đồ thị hàm số \[y = f\left( x \right)\]là
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây. Phương trình đường tiệm cận xiên của đồ thị hàm số là
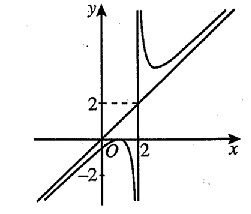
Tìm tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số \[y = \frac{{3 - x}}{{2x + 5}}\]
Cho hàm số \(y = \frac{{2x + 1}}{{x - 2}}\). Khẳng định nào dưới đây là đúng?
Viết phương trình các đường tiệm cận của đồ thị hàm số \(y = \frac{{x + 3}}{{2 - x}}\) ?
Đường thẳng \(x = - 1\) không là tiệm cận của đồ thị hàm số nào dưới đây?
III. Vận dụng
Đồ thị hàm số nào dưới đây có đường tiệm cận ngang qua điểm \(A\left( {2;3} \right)\)