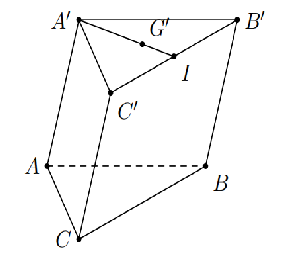
Cho hình lăng trụ \(ABC.A'B'C'\) đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c .\) Gọi \(G'\) là trọng tâm của tam giác \(A'B'C'\). Vectơ \(\overrightarrow {AG'} \) bằng
A. \(\overrightarrow {AG'} = \frac{1}{3}\left( {\overrightarrow a + 3\overrightarrow b + \overrightarrow c } \right).\)
B. \(\overrightarrow {AG'} = \frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow c } \right).\)
C. \(\overrightarrow {AG'} = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + 3\overrightarrow c } \right).\)
D. \(\overrightarrow {AG'} = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right).\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Gọi
\(I\) là trung điểm \(B'C'\). Vì \(G'\) là trọng tâm tam giác \(A'B'C'\) \( \Rightarrow \overrightarrow {A'G'} = \frac{2}{3}\overrightarrow {A'I} .\)
Mặt khác \(\overrightarrow {AG'} = \overrightarrow {AA'} + \overrightarrow {A'G'} = \overrightarrow {AA'} + \frac{2}{3}\overrightarrow {A'I} = \overrightarrow {AA'} + \frac{1}{3}\left( {\overrightarrow {A'B'} + \overrightarrow {A'C'} } \right)\)
\( = \overrightarrow {AA'} + \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {3\overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\).
III. Vận dụng
Một chiếc đèn chùm treo có khối lượng \(m = 5\) kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích \(SA,SB,SC,SD\) sao cho \(S.ABCD\) là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \). Biết \(\overrightarrow P = m.\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn \(10\)m/s2, \(\overrightarrow P \) là trọng lượng của vật có đơn vị kg.
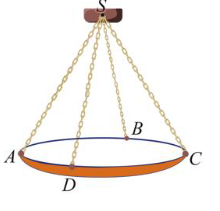
Khi đó:
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vectơ đồng phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|.\)
c) Độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm bằng \(50N\).
d) Độ lớn của lực căng cho mỗi sợi xích bằng \(\frac{{25\sqrt 3 }}{2}N\).
Số mệnh đề đúng trong các mệnh đề trên là:
Cho hình chóp \(S.ABC\). Tổng của hai vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {AB} \) là
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
I. Nhận biết
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\).
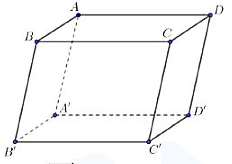
Vectơ nào sau đây cùng phương với \(\overrightarrow {BC} \) ?
Cho hình lập phương \(ABCD.A'B'C'D'\). Khẳng định nào sau đây là sai?
II. Thông hiểu
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M\) là trung điểm của cạnh \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a \), \(\overrightarrow {CB} = \overrightarrow b \), \(\overrightarrow {AA'} = \overrightarrow c \). Khẳng định nào sau đây đúng?
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) thỏa mãn: \(\left| {\overrightarrow a } \right| = 4\); \(\left| {\overrightarrow b } \right| = 3\); \(\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi \(\alpha \) là góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \). Chọn khẳng định đúng ?
Cho khối lập phương \(ABCD.A'B'C'D'\). Khi đó, góc giữa vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {AD} \) là
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
Cho hình lăng trụ \(ABC.A'B'C'\). Chọn khẳng định đúng trong các khẳng định dưới đây:
Cho tứ diện \(ABCD\). Gọi \(E,F\) là các điểm lần lượt thuộc các cạnh \(AB,CD\) sao cho \(AE = \frac{1}{3}AB,CF = \frac{1}{3}CD\). Tìm giá trị \(k\) với \(k \in \mathbb{R}\) thỏa mãn đẳng thức:
\(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AD} + k.\overrightarrow {BC} + \frac{1}{3}.\overrightarrow {AB} \).
Cho tứ diện \(ABCD\). Lấy \(G\) là trọng tâm tam giác \(BCD\). Phát biểu nào sau đây là sai?
Cho hình chóp \(S.ABC\) có \(AB = 4\), \(\widehat {BAC} = 60^\circ \), \(\overrightarrow {AB} .\overrightarrow {AC} = 6\). Khi đó độ dài \(\overrightarrow {AC} \) là
Cho hình lập phương \(ABCD.EFGH\) có cạnh bằng \(a\). Ta có: \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng:
Cho hình chóp \(S.ABC\) có \(SA = SB = SC\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {BC} \) ?