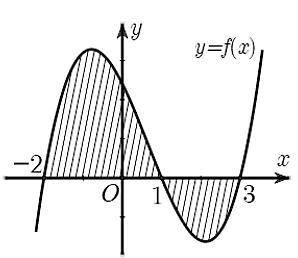
Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], trục hoành và hai đường thẳng \[x = - 3,x = 2\]. Đặt \[a = \int\limits_{ - 3}^1 {f\left( x \right)dx} ,{\rm{ }}b = \int\limits_1^2 {f\left( x \right)dx.} \]
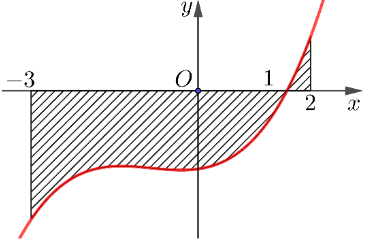
Mệnh đề nào dưới đây là đúng?
A. \[S = a + b.\]
B. \[S = a - b.\]
C. \[S = - a - b.\]
D. \[S = b - a.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Ta có: \[S = \int\limits_{ - 3}^2 {\left| {f\left( x \right)} \right|dx = } \int\limits_{ - 3}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} \]
\[ = - \int\limits_{ - 3}^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} \]\[ = b - a.\]
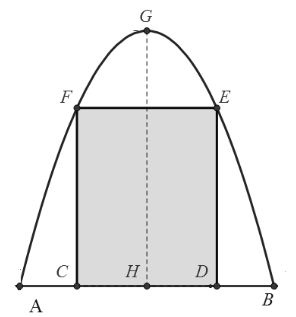
Chị Minh muốn làm một cái cổng hình parabol như hình vẽ dưới đây. Chiều cao \[GH = 4\] m, chiều rộng \[AB = 4\] m, \[AC = BD = 0,9\] m. Chi Minh làm hai cánh cổng khi đóng lại là hình chữ nhật \[CDEF\] tô đậm có giá là \[1200000\] đồng/m2, còn các phần để trắng để trang trí hoa có giá là \[900000\] đồng/m2. Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
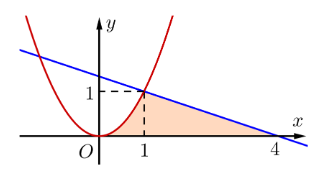
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2}\], \[y = - \frac{1}{3}x + \frac{4}{3}\] và trục hoành như hình vẽ sau:
III. Vận dụng
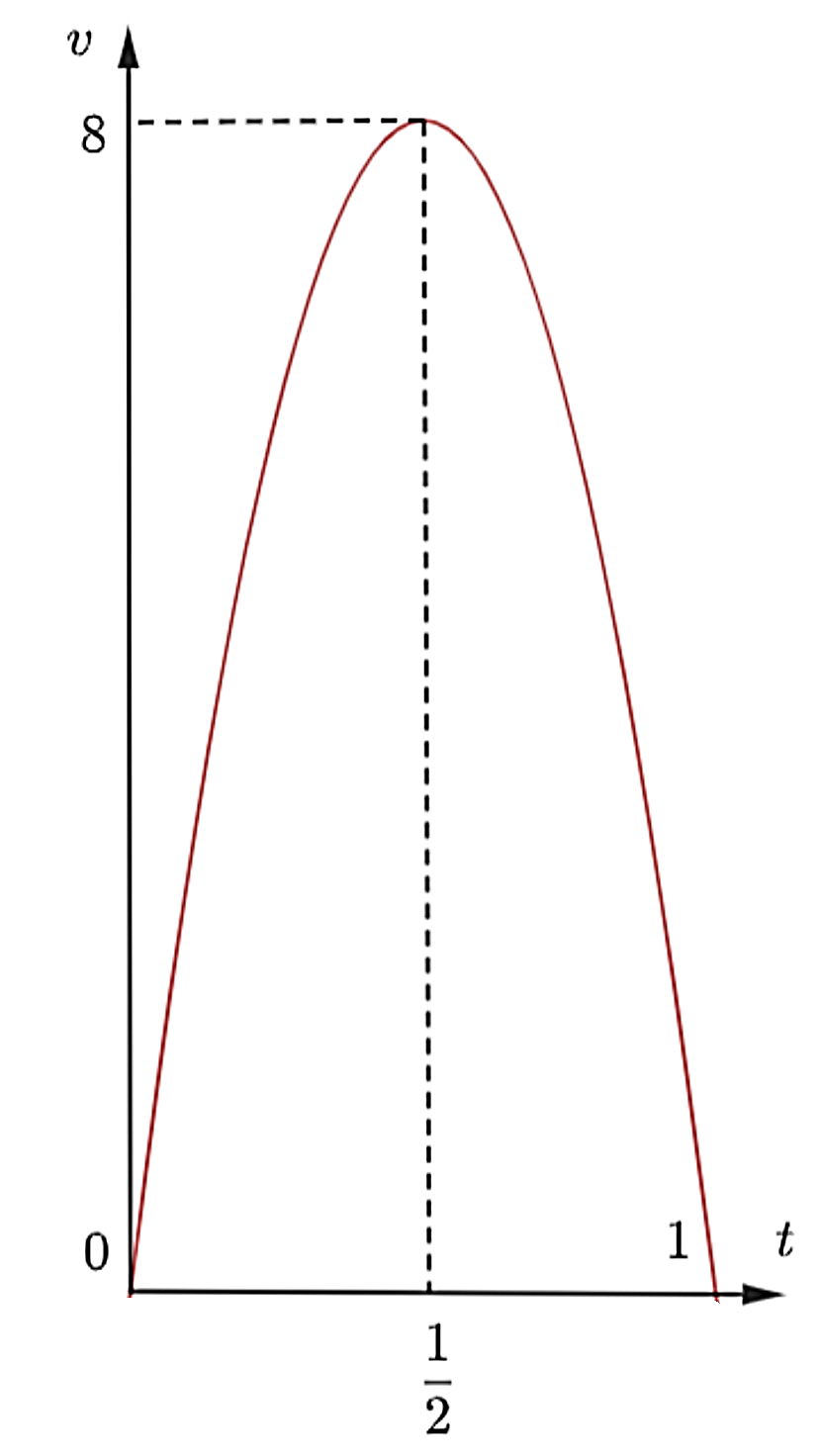
Một người chạy trong thời gian 1 giờ, vận tốc \[v\] (km/h) phụ thuộc vào thời gian t (h) có đồ thị là một phần parabol với đỉnh \[I\left( {\frac{1}{2};8} \right)\] và trục đối xứng song song với trục tung như hình bên. Tính quãng đường \[s\] người đó chạy được trong khoảng thời gian 45 phút, kể từ khi chạy?
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2} + 1,{\rm{ }}x = - 1,{\rm{ }}x = 2\] và trục hoành.
Cho hình phẳng D giới hạn bởi đường cong \[y = {e^x}\], trục hoành và các đường thẳng \[x = 0,x = 1\]. Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
Cho hình (H) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình \[y = \frac{{10}}{3}x - {x^2}\], \[y = \left\{ \begin{array}{l} - x,{\rm{ }}x \le 1\\x - 2{\rm{, }}x > 1\end{array} \right.\].
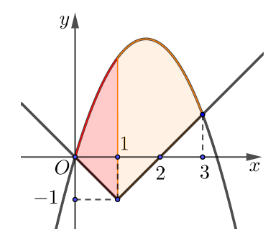
Diện tích của hình (H) bằng
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = \ln x,{\rm{ }}y = 1\] và hai đường thẳng \[x = 1,x = e\] bằng
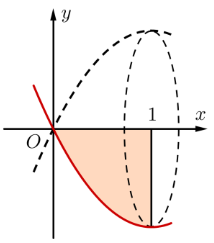
Cho hình phẳng (H) giới hạn bởi các đường \[y = {x^2} - 2x\], trục hoành, trục tung và đường thẳng \[x = 1.\] Tính thể tích V của khối tròn xoay khi quay (H) quanh trục \[Ox.\]
Diện tích \[S\] của hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] được tính theo công thức
</>
Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = {3^x}\], \[y = 0,x = 0,x = 2.\]Mệnh đề nào dưới đây là đúng?
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}.\] Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], \[y = 0,x = - 2,x = 3\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
Cho hình phẳng D giới hạn bởi đường cong \[y = {x^2} + 1\], trục hoành và các đường thẳng \[x = 0,x = 3\]. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
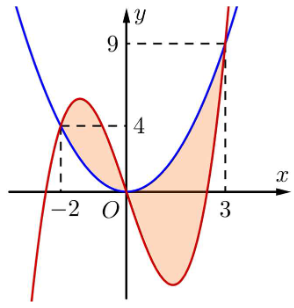
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = {x^3} - 6x,y = {x^2}\] (phần tô đậm trong hình sau) bằng:
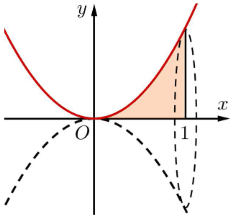
Cho hình (H) giới hạn bởi các đường \[y = {x^2},x = 1\] và trục hoành. Quay hình (H) quanh trục \[Ox\] ta được khối tròn xoay có thể tích là
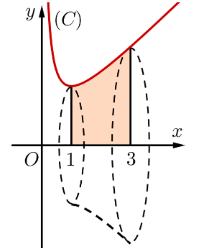
Gọi (H) là hình phẳng giới hạn bởi đồ thị \[\left( C \right):y = \frac{{{x^2} + 1}}{x}\], trục \[Ox\] và hai đường thẳng \[x = 1,x = 3\]. Thể tích V của vật thể tròn xoay khi (H) quay quanh trục \[Ox\] thỏa: