Trong không gian với hệ trục \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\). Biết \(A\left( {2;4;0} \right)\), \(B\left( {4;0;0} \right)\), \(C\left( { - 1;4; - 7} \right)\) và \(D'\left( {6;8;10} \right)\). Tìm tọa độ điểm \(B'\).
A. \(\left( {8;4;10} \right).\)
B. \(\left( {6;12;0} \right).\)
C. \(\left( {10;8;6} \right).\)
D. \(\left( {13;0;17} \right).\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Do \(ABCD.A'B'C'D'\) là hình hộp nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
Gọi \(D\left( {x;y;z} \right)\), suy ra \(\left\{ \begin{array}{l} - 1 - x = 4 - 2\\4 - y = 0 - 4\\ - 7 - z = 0 - 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = 8\\x = - 7\end{array} \right.\) ⇒ \(D\left( { - 3;8;7} \right)\).
Gọi \(B'\left( {{x_1};{y_1};{z_1}} \right)\), có \(\overrightarrow {DD'} = \overrightarrow {BB'} \) hay \(\left\{ \begin{array}{l}{x_1} - 4 = 6 - \left( { - 3} \right)\\{y_1} - 0 = 8 - 8\\{z_1} - 0 = 10 - \left( { - 7} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 13\\{y_1} = 0\\{z_1} = 17\end{array} \right.\) ⇒ \(B'\left( {13;0;17} \right)\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông có các cạnh bằng 1, \(SAD\) là tam giác đều và nằm trong mặt phẳng với đáy. Gọi \(O\), \(M\) và \(N\) lần lượt là trung điểm của \(AD\), \(BC\) và \(CD\). Thiết lập hệ trục tọa độ \(Oxyz\) như hình vẽ.
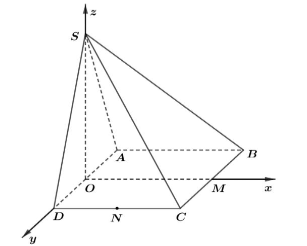
a) Tọa độ các điểm \(A,B\) là \(A\left( {0; - \frac{1}{2};0} \right),B\left( {1; - \frac{1}{2};0} \right).\)
b) Tọa độ các điểm \(C,D\) là \(C\left( {1;\frac{1}{2};0} \right),D\left( {0;\frac{1}{2};0} \right).\)
c) Tọa độ điểm \(S\) là điểm \(S\left( {0;0;\frac{{\sqrt 3 }}{2}} \right).\)
d) Tọa độ các điểm \(M,N\) là \(M\left( {1;0;0} \right),N\left( {\frac{1}{2};\frac{1}{2};0} \right).\)
Khi đó, số mệnh đề đúng trong các mệnh đề là:
Trong không gian với hệ trục \(Oxyz\), cho ba điểm \(A\left( { - 1;2; - 3} \right)\), \(B\left( {1;0;2} \right)\), \(C\left( {x;y;7} \right)\) sao cho \(\overrightarrow {AB} = \overrightarrow {BC} \). Khi đó \(x + y\) bằng
Trong không gian với hệ trục \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có điểm \(A\) trùng với gốc tọa độ \(O\), điểm \(B\) nằm trên tia \(Ox\), điểm \(D\) nằm trên tia \(Oy\), điểm \(A'\) nằm trên tia \(Oz\). Biết \(AB = 2,AD = 4,AA' = 3\). Gọi tọa độ \(C'\) là \(\left( {a;b;c} \right)\) khi đó biểu thức \(a + b - c\) có giá trị là
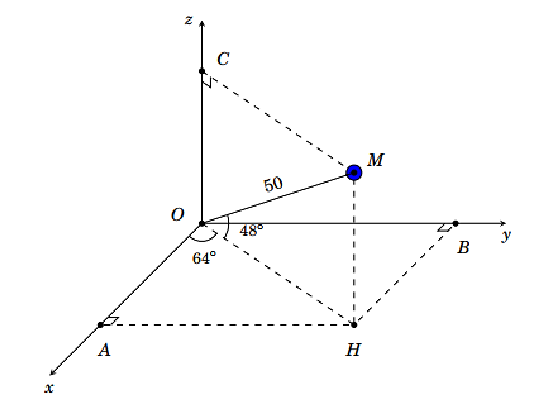
Ở một sân bay, vị trí của máy bay được xác định bởi điểm \(M\) trong không gian \(Oxyz\) như hình bên. Gọi \(H\) là hình chiếu vuông góc của \(M\) xuống mặt phẳng \(\left( {Oxy} \right)\). Biết \(OM = 70,\left( {\overrightarrow i ,\overrightarrow {OH} } \right) = 64^\circ \), \(\left( {\overrightarrow {OH} ,\overrightarrow {OM} } \right) = 48^\circ \). Tìm tọa độ điểm \(M\).
Trong không gian \(Oxyz\), cho \(A\left( {2; - 1;0} \right)\) và \(B\left( {1;1; - 3} \right)\). Vectơ \(\overrightarrow {AB} \) có tọa độ là
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(A\left( {2;3; - 1} \right)\) trên mặt phẳng \(\left( {Oxz} \right)\) có tọa độ là
Trong không gian với hệ trục \(Oxyz\), cho hình bình hành \(ABCD\) có tâm \(I\) có tọa độ các đỉnh \(B\left( {3;1;0} \right)\), \(D\left( {0;4; - 6} \right)\). Tọa độ điểm \(I\) là
Trong không gian \(Oxyz\), cho \(M\left( {8;4;3} \right)\). Khi đó:
a) Hình chiếu vuông góc của \(M\) trên trục \(Ox\) là điểm \(\left( {0;4;3} \right)\).
b) Hình chiếu vuông góc của \(M\) trên trục \(Oz\) là điểm \(\left( {0;0;3} \right)\).
c) Hình chiếu vuông góc của \(M\) trên trục \(Oxz\) là điểm \(\left( {8;0;3} \right)\).
d) \(\overrightarrow {OM} = 8\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k .\)
Số mệnh đề đúng trong các mệnh đề trên là:
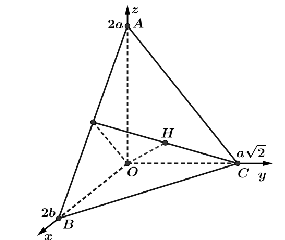
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc và \(OA = OB = 2a\), \(OC = a\sqrt 2 \). Khi đó vectơ \(\overrightarrow {AB} \left( {m;n;p} \right)\). Khi \(a = 1\) hãy tính giá trị của biểu thức \(T = m + n + p.\)
I. Nhận biết
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(A\left( {3;4;1} \right)\) lên trục \(Ox\) có tọa độ là
Trong không gian với hệ trục \(Oxyz\), cho hai điểm \(A\left( {2;1;1} \right)\), \(B\left( { - 1;2;1} \right)\). Tìm tọa độ của điểm \(A'\) đối xứng với điểm \(A\) qua điểm \(B\) ?
Trong không gian \(Oxyz\), cho \(I\left( {1;2;3} \right)\). Điểm đối xứng với \(A\) qua trục \(Oz\) có tọa độ là
II. Thông hiểu
Trong không gian với hệ trục \(Oxyz\), cho hình bình hành \(ABCD\) và các đỉnh có tọa độ lần lượt là \(A\left( {3;1;2} \right),B\left( {1;0;1} \right),C\left( {2;3;0} \right)\). Tọa độ đỉnh \(D\) là
Trong không gian với hệ trục \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {1;2;3} \right)\) và \(\overrightarrow v = 2\overrightarrow i + a\overrightarrow j + 6\overrightarrow k \). Tìm giá trị của tham số a để \(\overrightarrow u = \frac{1}{2}\overrightarrow v \).
Trong không gian với hệ trục \(Oxyz\), cho điểm \(M\left( {1;2;3} \right)\). Gọi \(H\) là hình chiếu vuông góc của \(M\) lên mặt phẳng \(\left( {Oxy} \right)\). Tọa độ của \(H'\) đối xứng với \(H\) qua mặt phẳng \(\left( {Oxz} \right)\) là