Trong không gian \(Oxyz\), cho hình thang \(ABCD\) vuông tại \(A\) và \(B\). Ba đỉnh \(A\left( {1;2;1} \right)\), \(B\left( {2;0; - 1} \right)\), \(C\left( {6;1;0} \right)\). Hình thang có diện tích bằng \(6\sqrt 2 \). Giả sử đỉnh \(D\left( {a;b;c} \right)\), tìm mệnh đề đúng.
A. \(a + b + c = 6.\)
B. \(a + b + c = 5.\)
C. \(a + b + c = 8.\)
D. \(a + b + c = 7.\)
Giải bởi Vietjack
Đáp án đúng là: A
Ta có: \(\overrightarrow {AB} = \left( {1; - 2; - 2} \right) \Rightarrow AB = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} = 3\);
\(\overrightarrow {BC} = \left( {4;1;1} \right) \Rightarrow BC = \sqrt {{4^2} + {1^2} + {1^2}} = 3\sqrt 2 \).
Theo giả thiết \(ABCD\) là hình thang vuông tại \(A\) và \(B\) và có diện tích bằng \(6\sqrt 2 \) nên
\(\frac{1}{2}AB\left( {AD + BC} \right) = 6\sqrt 2 \Leftrightarrow \frac{1}{2}.3\left( {AD + 3\sqrt 2 } \right) = 6\sqrt 2 \Leftrightarrow AD = \sqrt 2 \Rightarrow AD = \frac{1}{3}BC\).
Do \(ABCD\) là hình thang vuông tại \(A\) và \(B\) nên \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {BC} \).
Suy ra \(\left\{ \begin{array}{l}a - 1 = \frac{4}{3}\\b - 2 = \frac{1}{3}\\c - 1 = \frac{1}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{7}{3}\\b = \frac{7}{3}\\c = \frac{4}{3}\end{array} \right. \Rightarrow a + b + c = 6\).
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất cách điểm xuất phát 2 km về phía nam và 1 km về phía đông, đồng thời cách mặt đất 0,5 km. chiếc thứ hai mằm cách điểm xuất phát 1 km về phía bắc và 1,5 km về phía tây, đồng thời cách mặt đất 0,8 m. Chọn hệ trục \(Oxyz\) với O là gốc đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất với trục \(Ox\) hướng về phía nam, trục \[Oy\] hướng về phía đông và trục \(Oz\) hướng thẳng đứng lên trời, đơn vị đo lấy theo kilomet.
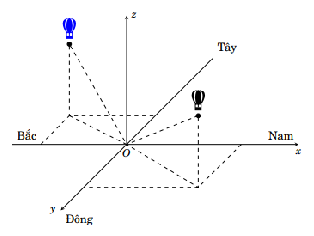
Khi đó:
a) Với hệ tọa độ đã chọn, tọa độ khinh khí cầu thứ nhất là \(\left( {2;1;0,5} \right)\).
b) Với hệ tọa độ đã chọn, tọa độ khinh khí cầu thứ hai là \(\left( { - 1,5; - 1;0,8} \right)\).
c) Khoảng cách từ điểm xuất phát đến khinh khí cầu thứ nhất bằng \(\sqrt {21} \) km.
d) Khoảng cách hai chiếc khinh khí cầu là 3,92 km (Kết quả làm tròn đến hàng phần trăm).
Số khẳng định đúng trong các khẳng định trên là:
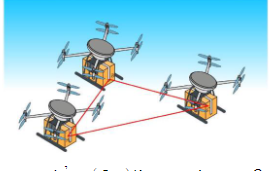
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian \(Oxyz\), một đội gồm ba drone giao hàng \(A,B,C\) đang có tọa độ là \(A\left( {1;1;1} \right)\), \(B\left( {5;7;9} \right)\), \(C\left( {9;11;4} \right)\). Gọi \({d_1},{d_2},{d_3}\) lần lượt là khoảng cách của mỗi cặp drone giao hàng trên. Tính \({d_1} + {d_2} + {d_3}\). (Kết quả làm tròn đến hàng đơn vị).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {1;2; - 1} \right)\), \(B\left( {2; - 1;3} \right)\), \(C\left( { - 4;7;5} \right)\). Gọi \(D\left( {a;b;c} \right)\) là chân đường phân giác trong góc \(B\) của tam giác \(ABC\). Giá trị \(a + b + 2c\) bằng
II. Thông hiểu
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {1;2;3} \right)\) và \(\overrightarrow v = \left( {4; - 5;6} \right)\). Vectơ \(2\overrightarrow u - 3\overrightarrow v \) cùng phương với vectơ nào?
Trong không gian \(Oxyz\), cho ba điểm \(M\left( {2; - 3; - 1} \right)\), \(N\left( {0;3;1} \right)\), \(P\left( {1;m - 1;2} \right)\). Với giá trị nào của \(m\) thì tam giác \(MNP\) vuông tại \(N\)?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;2; - 5} \right)\), \(B\left( {1;2;4} \right)\), \(C\left( {2;5; - 2} \right)\). Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {0;2;1} \right)\) và \(B\left( {3; - 2;1} \right)\). Độ dài đoạn thẳng \(AB\) bằng
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( { - 1 - 1;0} \right)\) và \(\overrightarrow b = \left( {0; - 1;0} \right)\). Góc giữa hai vectơ này là:
Trong không gian \(Oxyz\), cho các điểm \(A\left( {1;3;5} \right)\), \(B\left( {1;1;3} \right)\), \(C\left( {4; - 2;3} \right)\).
Khi đó:
a) Tọa độ trung điểm \(BC\) là \(\left( {\frac{5}{2}; - \frac{1}{2};3} \right)\).
b) Độ dài đoạn thẳng \(BC\) là \(3\sqrt 2 \).
c) Côsin \(\widehat {BAC}\) bằng \(\frac{{7\sqrt {19} }}{{38}}\).
d) Gọi \(D\) là đỉnh thứ tư của hình bình hành \(ABCD\). Tọa độ hình chiếu của trọng tâm tam giác \(ABD\) lên mặt phẳng \(Oyz\) là \(\left( {2;0;0} \right)\).
Số mệnh đề đúng trong các mệnh đề trên là:
I. Nhận biết
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow a = \left( { - 2;6;2} \right)\). Vectơ \(\frac{3}{2}\overrightarrow a \) có tọa độ là
Trong không gian \(Oxyz\), cho hai điểm \(M\left( {1; - 2;2} \right)\) và \(N\left( {1;0;4} \right)\). Tọa độ trung điểm của đoạn thẳng \(MN\) là
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow u = \left( {1; - 2;3} \right)\). Vectơ nào sau đây cùng phương với vectơ \(\overrightarrow u \) ?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {0;1; - 1} \right)\), \(B\left( {1;2;0} \right)\), \(\left( {m;n;0} \right)\). Giá trị \(m,n\) sao cho ba điểm \(A,B,C\) thẳng hàng:
Trong không gian \(Oxyz\), cho ba điểm \(A\left( { - 1; - 2;3} \right)\), \(B\left( {0;3;1} \right)\), \(C\left( {4;2;2} \right)\). Giá trị \(\cos \left( {\widehat {BAC}} \right)\) bằng
Trong không gian \(Oxyz\), cho điểm \(G\left( {1; - 2;3} \right)\) và ba điểm \(A\left( {a;0;0} \right)\), \(B\left( {0;b;0} \right)\), \(C\left( {0;0;c} \right)\). Biết \(G\) là trọng tâm của của tam giác \(ABC\) thì \(a + b + c\) bằng
