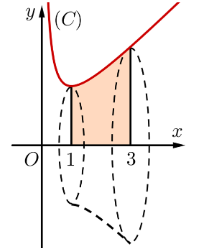
Gọi (H) là hình phẳng giới hạn bởi đồ thị \[\left( C \right):y = \frac{{{x^2} + 1}}{x}\], trục \[Ox\] và hai đường thẳng \[x = 1,x = 3\]. Thể tích V của vật thể tròn xoay khi (H) quay quanh trục \[Ox\] thỏa:
A. \[16 < V < 17.\]
B. \[41 < V < 42.\]
C. \[13 < V < 14.\]
D. \[5 < V < 6.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có: \[V = \pi \int\limits_1^3 {{{\left( {\frac{{{x^2} + 1}}{x}} \right)}^2}} dx = \pi \int\limits_1^3 {\left( {{x^2} + 2 + \frac{1}{{{x^2}}}} \right)dx} \]
\[ = \left. {\pi \left( {\frac{{{x^3}}}{3} + 2x - \frac{1}{x}} \right)} \right|_1^3 = \frac{{40\pi }}{3} \approx 41,89\].
Vậy \[41 < V < 42.\]
Cho hình (H) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình \[y = \frac{{10}}{3}x - {x^2}\], \[y = \left\{ \begin{array}{l} - x,{\rm{ }}x \le 1\\x - 2{\rm{, }}x > 1\end{array} \right.\].
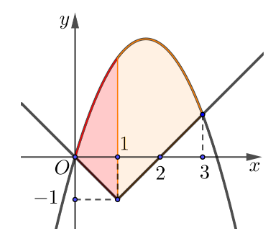
Diện tích của hình (H) bằng
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = \ln x,{\rm{ }}y = 1\] và hai đường thẳng \[x = 1,x = e\] bằng
Cho hình phẳng D giới hạn bởi đường cong \[y = \sqrt {2 + \cos x} \], trục hoành và các đường thẳng \[x = 0,x = \frac{\pi }{2}.\] Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng:
Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = {3^x}\], \[y = 0,x = 0,x = 2.\]Mệnh đề nào dưới đây là đúng?
Một li rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc cốc thành 2 phần bằng nhau) là một đường parabol.
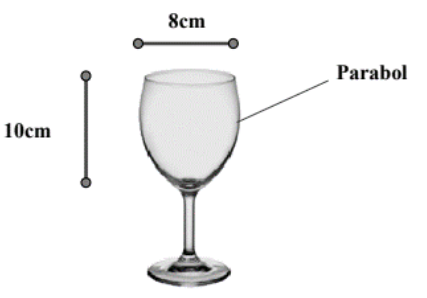
Thể tích tối đa mà cốc có thể chứa được là (làm tròn kết quả đến hai chữ số thập phân).
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2} + 1,{\rm{ }}x = - 1,{\rm{ }}x = 2\] và trục hoành.
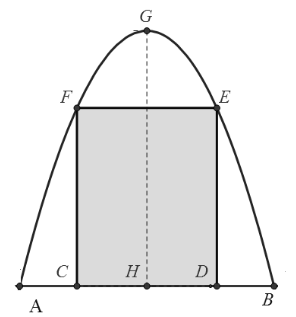
Chị Minh muốn làm một cái cổng hình parabol như hình vẽ dưới đây. Chiều cao \[GH = 4\] m, chiều rộng \[AB = 4\] m, \[AC = BD = 0,9\] m. Chi Minh làm hai cánh cổng khi đóng lại là hình chữ nhật \[CDEF\] tô đậm có giá là \[1200000\] đồng/m2, còn các phần để trắng để trang trí hoa có giá là \[900000\] đồng/m2. Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
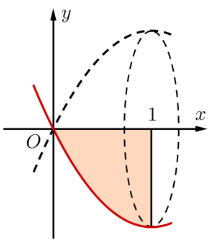
Cho hình phẳng D giới hạn bởi đường cong \[y = {e^x}\], trục hoành và các đường thẳng \[x = 0,x = 1\]. Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
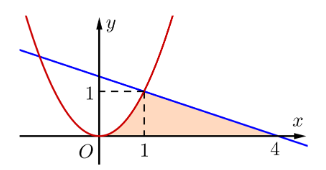
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2}\], \[y = - \frac{1}{3}x + \frac{4}{3}\] và trục hoành như hình vẽ sau:
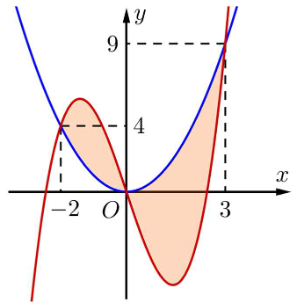
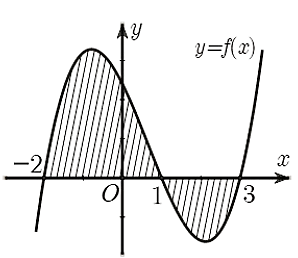
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}.\] Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], \[y = 0,x = - 2,x = 3\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
Cho hình phẳng D giới hạn bởi đường cong \[y = {x^2} + 1\], trục hoành và các đường thẳng \[x = 0,x = 3\]. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
Cho hình phẳng (H) giới hạn bởi các đường \[y = {x^2} - 2x\], trục hoành, trục tung và đường thẳng \[x = 1.\] Tính thể tích V của khối tròn xoay khi quay (H) quanh trục \[Ox.\]
I. Nhận biết
Thể tích \[V\] của khối tròn xoay giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] khi quay quanh trục \[Ox\] là:
Diện tích \[S\] của hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] được tính theo công thức
</>
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = {x^3} - 6x,y = {x^2}\] (phần tô đậm trong hình sau) bằng: