Một li rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc cốc thành 2 phần bằng nhau) là một đường parabol.
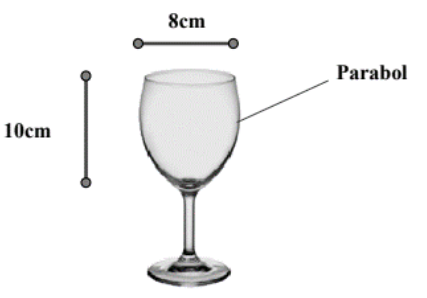
Thể tích tối đa mà cốc có thể chứa được là (làm tròn kết quả đến hai chữ số thập phân).
A. \[V \approx 320\] cm3.
B. \[V \approx 1005,31\] cm3.
C. \[V \approx 251,33\] cm3.
D. \[V \approx 502,65\] cm3.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Gắn phần miệng li đựng nước vào hệ trục tọa độ, với đỉnh trùng với gốc tọa độ.
Lúc này, ta được parabol đi qua các điểm (0; 0), (−4; 10); (4; 10).
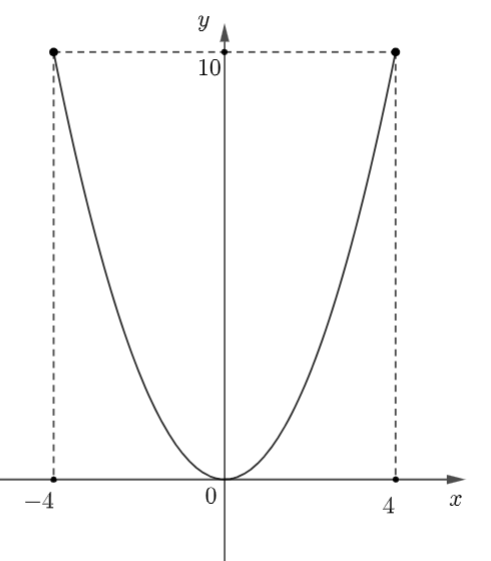
Gọi phương trình parabol là: \[y = a{x^2} + bx + c\] \[\left( {a \ne 0} \right)\].
Ta có: \[\left\{ \begin{array}{l}c = 0\\16a - 4b + c = 10\\16a + 4b + c = 10\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 0\\a = \frac{5}{8}\\b = 0\end{array} \right.\].
Vậy \[y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y \Leftrightarrow x = \sqrt {\frac{8}{5}y} \]
Thể tích tối đa mà cốc có thể chứa nước là
\[V = \pi {\int\limits_0^{10} {\left( {\sqrt {\frac{8}{5}} y} \right)} ^2}dy = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)dy = \left. {\pi \frac{4}{5}{y^2}} \right|_0^{10}} = 80\pi \approx 251,33\] cm3.
Cho hình (H) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình \[y = \frac{{10}}{3}x - {x^2}\], \[y = \left\{ \begin{array}{l} - x,{\rm{ }}x \le 1\\x - 2{\rm{, }}x > 1\end{array} \right.\].
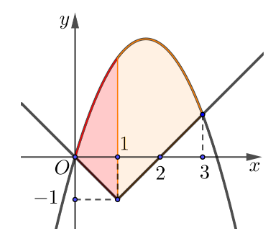
Diện tích của hình (H) bằng
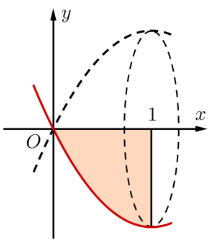
Cho hình phẳng (H) giới hạn bởi các đường \[y = {x^2} - 2x\], trục hoành, trục tung và đường thẳng \[x = 1.\] Tính thể tích V của khối tròn xoay khi quay (H) quanh trục \[Ox.\]
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = \ln x,{\rm{ }}y = 1\] và hai đường thẳng \[x = 1,x = e\] bằng
Cho hình phẳng D giới hạn bởi đường cong \[y = \sqrt {2 + \cos x} \], trục hoành và các đường thẳng \[x = 0,x = \frac{\pi }{2}.\] Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng:
I. Nhận biết
Thể tích \[V\] của khối tròn xoay giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] khi quay quanh trục \[Ox\] là:
Diện tích \[S\] của hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] được tính theo công thức
</>
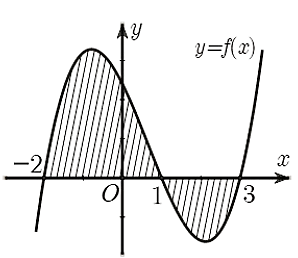
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}.\] Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], \[y = 0,x = - 2,x = 3\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
II. Thông hiểu
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {\left( {x - 2} \right)^2} - 1\], trục hoành và hai đường thẳng \[x = 1,x = 2\] bằng
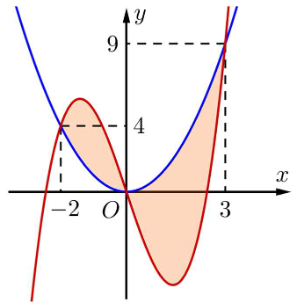
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = {x^3} - 6x,y = {x^2}\] (phần tô đậm trong hình sau) bằng:
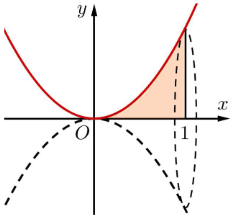
Cho hình (H) giới hạn bởi các đường \[y = {x^2},x = 1\] và trục hoành. Quay hình (H) quanh trục \[Ox\] ta được khối tròn xoay có thể tích là
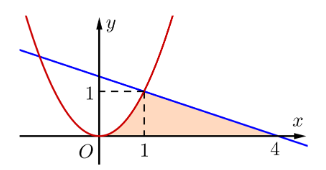
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2}\], \[y = - \frac{1}{3}x + \frac{4}{3}\] và trục hoành như hình vẽ sau:
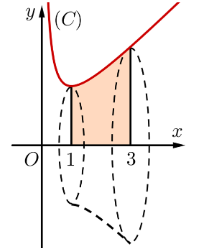
Gọi (H) là hình phẳng giới hạn bởi đồ thị \[\left( C \right):y = \frac{{{x^2} + 1}}{x}\], trục \[Ox\] và hai đường thẳng \[x = 1,x = 3\]. Thể tích V của vật thể tròn xoay khi (H) quay quanh trục \[Ox\] thỏa:
Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], trục hoành và hai đường thẳng \[x = - 3,x = 2\]. Đặt \[a = \int\limits_{ - 3}^1 {f\left( x \right)dx} ,{\rm{ }}b = \int\limits_1^2 {f\left( x \right)dx.} \]
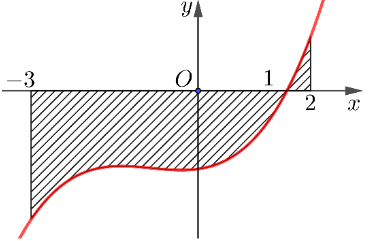
Mệnh đề nào dưới đây là đúng?
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2} + 1,{\rm{ }}x = - 1,{\rm{ }}x = 2\] và trục hoành.
Cho hình phẳng D giới hạn bởi đường cong \[y = {x^2} + 1\], trục hoành và các đường thẳng \[x = 0,x = 3\]. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng