Một nhóm học sinh có 6 bạn nam và 5 bạn nữ. Hỏi có bao nhiêu cách chọn ra 5 học sinh trong đó có cả nam và nữ?

Cho X là biến ngẫu nhiên tuân theo luật phân phối đều liên tục X∼U([a;b]). Giá trị P(X∈[a−1;b+1]) bằng:

C.

D.

Một hộp đựng 5 viên bi màu xanh, 7 viên bi màu vàng. Có bao nhiêu cách lấy ra 6 viên bi bất kỳ?

Có bao nhiêu cách lấy hai con bài từ cỗ bài tú lơ khơ gồm 52 con?

Biến ngẫu nhiên X tuân theo luật phân phối nhị thức: X∼B(n,p).P(X=x), với 0≤x≤n, bằng:

Có 15 đội bóng đá thi đấu theo thể thức vòng tròn tính điểm. Hỏi cần phải tổ chức bao nhiêu trận đấu?

Có bao nhiêu cách cắm 3 bông hoa giống nhau vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông)?

Cho X∼B(5;0.25). Giá trị P(X > 3) bằng:

Trong mặt phẳng, cho 6 điểm phân biệt sao cho không có ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?

Cho mặt phẳng chứa đa giác đều (H) có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của (H). Hỏi có bao nhiêu tam giác có đúng 1 cạnh là cạnh của (H).

Số giao điểm tối đa của 10 đường thẳng phân biệt là:

Cho hai biến ngẫu nhiên X có phân phối chuẩn , Y có phân phối chuẩn , X độc lập với Y. Thống kê  có quy luật phân phối?

Với đa giác lồi 10 cạnh thì số đường chéo là:

Trong mặt phẳng có bao nhiêu hình chữ nhật được tạo thành từ bốn đường thẳng phân biệt song song với nhau và năm đường thẳng phân biệt vuông góc với bốn đường thẳng song song đó?

Một lớp có 15 học sinh nam và 20 học sinh nữ. Có bao nhiêu cách chọn 5 bạn học sinh sao cho trong đó có đúng 3 học sinh nữ?

Cho hai biến ngẫu nhiên X có phân phối chuẩn 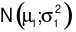, Y có phân phối chuẩn 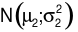, X độc lập với Y. Thống kê 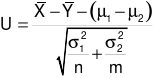có quy luật phân phối