Giải bởi Vietjack
Phương pháp giải
+ Gọi \(M\left( {x;y;z} \right)\) và \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên \({\rm{mp}}\left( P \right)\).
+ Chứng minh \(M\) luôn thuộc một đường tròn cố định.
+ Gọi \(E\) là hình chiếu của \(I\) lên \(\left( P \right)\), tìm \(E\).
+ Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \({\rm{mp}}\left( P \right)\), tìm \(H\).
+ vì \(O{M^2} = O{H^2} + H{M^2}\) nên \(OM_{{\rm{max}}}^2 \Leftrightarrow HM_{{\rm{max}}}^2\), tính \(O{M^2}\) max.
Phương pháp giải các bài toán về mặt cầu và mặt phẳng
Lời giải
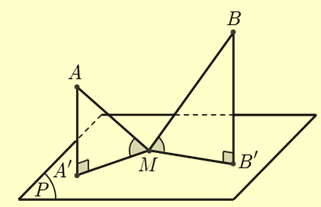
Nhận thấy đường thẳng \(AB\) không vuông góc với \({\rm{mp}}\left( P \right)\) và
\(\left( { - 1 + 0 - 0 + 2} \right).\left( {1 + 0 - 1 + 2} \right) > 0\) nên \(A,B\) nằm cùng phía so với \(\left( P \right)\).
Gọi \(M\left( {x;y;z} \right)\) và \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên \({\rm{mp}}\left( P \right)\).
Vì các đường thẳng \(MA,MB\) cùng tạo với \({\rm{mp}}\left( P \right)\) các góc bằng nhau nên \(\widehat {AMA'} = \widehat {BMB'}\)
\( \Rightarrow {\rm{\Delta }}AMA'\,\,{\rm{\Delta }}BMB' \Rightarrow \frac{{MA}}{{MB}} = \frac{{AA'}}{{BB'}} = \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}} = \frac{{\left| { - 1 + 2} \right|}}{{\left| {1 - 1 + 2} \right|}} = \frac{1}{2}\)
\( \Leftrightarrow MB = 2MA \Leftrightarrow M{B^2} = 4M{A^2} \Leftrightarrow {(x - 1)^2} + {y^2} + {(z - 1)^2}\)
\( = 4\left[ {{{(x + 1)}^2} + {y^2} + {z^2}} \right]\)
\( \Leftrightarrow 3{x^2} + 3{y^2} + 3{z^2} + 10x + 2z + 2 = 0 \Leftrightarrow {x^2} + {y^2} + {z^2} + \frac{{10}}{3}x + \frac{2}{3}z + \frac{2}{3} = 0\).
Suy ra \(M\) nằm trên mặt cầu \(\left( S \right)\) tâm \(I\left( { - \frac{5}{3};0; - \frac{1}{3}} \right)\), bán kính \(R = \sqrt {{{\left( { - \frac{5}{3}} \right)}^2} + {{\left( { - \frac{1}{3}} \right)}^2} - \frac{2}{3}} = \frac{{2\sqrt 5 }}{3}\).
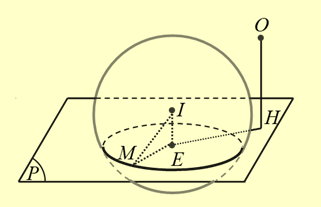
Vì \(\left\{ {\begin{array}{*{20}{l}}{M \in \left( P \right)}\\{M \in \left( S \right)}\end{array} \Rightarrow M \in \left( C \right)} \right.\), với \(\left( C \right) = \left( P \right) \cap \left( S \right)\).
Ta có \(d\left( {I,\left( P \right)} \right) = \frac{{\left| { - \frac{5}{3} + \frac{1}{3} + 2} \right|}}{{\sqrt 3 }} = \frac{2}{{3\sqrt 3 }}\).
Gọi \(E\) là hình chiếu của \(I\) lên \(\left( P \right)\).
Đường tròn \(\left( C \right)\) có tâm là \(E\) và bán kính bằng \(r = \sqrt {{R^2} - {d^2}\left( {I,\left( P \right)} \right)} = \)\(\sqrt {\frac{{20}}{9} - \frac{4}{{27}}} = \frac{{2\sqrt {42} }}{9}\).
Đường thẳng \(IE\) đi qua điểm \(I\) nhận vectơ pháp tuyến của \({\rm{mp}}\left( P \right)\) là \(\overrightarrow {{n_{\left( P \right)}}} = \left( {1;1; - 1} \right)\) làm vectơ chỉ phương nên có phương trình \(IE:\left\{ {\begin{array}{*{20}{l}}{x = - \frac{5}{3} + t}\\{y = t}\\{z = - \frac{1}{3} - t}\end{array} \Rightarrow E\left( { - \frac{5}{3} + t;t; - \frac{1}{3} - t} \right)} \right.\).
\(E \in \left( P \right) \Leftrightarrow - \frac{5}{3} + t + t + \frac{1}{3} + t + 2 = 0 \Leftrightarrow t = - \frac{2}{9} \Leftrightarrow E\left( { - \frac{{17}}{9}; - \frac{2}{9}; - \frac{1}{9}} \right)\).
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \({\rm{mp}}\left( P \right)\).
Phương trình đường thẳng \(OH:\left\{ {\begin{array}{*{20}{l}}{x = t'}\\{y = t'}\\{z = - t'}\end{array} \Rightarrow H\left( {t';t'; - t'} \right)} \right.\).
\(H\left( {t';t'; - t'} \right) \in \left( P \right) \Leftrightarrow t' + t' + t' + 2 = 0 \Leftrightarrow t' = - \frac{2}{3} \Leftrightarrow H\left( { - \frac{2}{3}; - \frac{2}{3};\frac{2}{3}} \right)\).
\(\overrightarrow {HE} = \left( { - \frac{{11}}{9};\frac{4}{9}; - \frac{7}{9}} \right) \Rightarrow HE = \sqrt {\frac{{121}}{{81}} + \frac{{16}}{{81}} + \frac{{49}}{{81}}} = \frac{{\sqrt {186} }}{9}\).
vì \(O{M^2} = O{H^2} + H{M^2}\) nên \(OM_{{\rm{max}}}^2 \Leftrightarrow HM_{{\rm{max}}}^2\)
Mà \(H{M_{{\rm{max}}}} = HE + r = \frac{{\sqrt {186} + 2\sqrt {42} }}{9}\).
Suy ra \(OM_{{\rm{max}}}^2 = \frac{4}{3} + {\left( {\frac{{\sqrt {186} + 2\sqrt {42} }}{9}} \right)^2} = \frac{4}{3} + \frac{{354 + 24\sqrt {217} }}{{81}} = \frac{{462 + 24\sqrt {217} }}{{81}}\).
Do đó \(a = 462,b = 217,c = 81\).
Vậy \(a + b + c = 760\).
Chọn C
Hoàn thành câu hỏi bằng cách chọn đáp án đúng hoặc sai.
Hai ông ấm – con trai cụ Kép là những người con hiếu thảo, luôn cố gắng làm cha vui lòng khi toại được sở thích của mình.
Đúng hay sai?
Với tính cách của cụ Kép, theo em vì sao cụ KHÔNG trồng lan Bạch ngọc?
Trong thí nghiệm Young về giao thoa ánh sáng, khoảng vân sẽ thay đổi thế nào khi ta thay nguồn sáng đơn sắc có bước sóng λ bằng ánh sáng đơn sắc có bước sóng là 1,2λ? Nếu khoảng cách từ hai khe đến màn quan sát giữ cố định, ta phải thay đổi khoảng cách giữa hai khe như thế nào để khoảng vẫn lại có độ lớn như ban đầu?
Các nhận định dưới đây đúng hay sai?
|
|
ĐÚNG |
SAI |
|
A. Trên bề mặt virus cúm có hai loại kháng nguyên là gai H và gai N. |
||
|
B. Gai H khi xâm nhập vào cơ thể vật chủ sẽ làm ngưng kết hồng cầu vật chủ. |
||
|
C. Gai N làm giảm khả năng tự bảo vệ của đường hô hấp vật chủ. |
||
|
D. Trong cơ thể người, không có kháng thể kháng các kháng nguyên virus cúm. |
uống rượu thưởng trăng, làm thơ, nấu kẹo mạch nha, cúng bái, bình thơ, uống rượu thưởng hoa
Không khí Tết cổ truyền được miêu tả qua những chi tiết: Cụ Kép cùng con cháu quây quần chăm chút cho vườn lan nở đúng dịp Tết, _______ ướp hương lan, _______ đêm giao thừa, _______ cùng những người bạn già, _______ và thưởng thức cái không khí êm đềm của mùa xuân.
Điền số thích hợp vào chỗ trống (Làm tròn đến chữ số thập phân thứ nhất)
pH trung gian mà tại đó người ta mong chờ có sự đổi màu của chỉ thị phenolphtalein là _______.
Một trong hai khe hẹp được làm mờ sao cho nó chỉ truyền ánh sáng được bằng ½ cường độ sáng của khe còn lại. Kết quả xảy ra là:
Để tổng hợp 18 mol phenolphtalein theo quá trình đã được Adolf van Bayer đã phát hiện ra vào năm 1871 cần bao nhiêu gam chất phản ứng? Biết phản ứng có hiệu suất 90%.
Dựa vào văn bản, điền hai từ ngữ phù hợp, mỗi từ không quá hai tiếng vào chỗ trống.
Nhan đề “Hương cuội” trong văn cảnh truyện ngắn này có nghĩa là mùi hương của _______. Nó được chọn làm _______ và được ướp hương lan nên có mùi hương của hoa lan.
Cho hai từ: sóng, hạt. Hay chọn từ thích hợp điền vào chỗ trống:
Giao thoa ánh sáng là thí nghiệm chứng minh ánh sáng có tính chất _______
Kéo thả đáp án chính xác vào chỗ trống
antigenic shift, antigenic drift
Để nghiên cứu độc lực của một chủng virus cúm, người ta cho chủng đó lây nhiễm vào cơ thể vật chủ thí nghiệm. Sau một thời gian, người ta phát hiện trong cơ thể vật chủ thí nghiệm, người ta phát hiện một biến chủng virus cúm mới khác với chủng virus cúm ban đầu.Biến chủng virus cúm mới có thể được hình thành từ cơ chế _________.
Hai thanh nam châm A và B được đặt như hình. Trong các cách sắp xếp sau, những trường hợp nào 2 thanh hút nhau.
Cho biết rằng lực kháng từlà đại lượng quan trọng đặc trưng cho tính từ cứng của vật liệu từ cứng. Vì vật liệu từ cứng là khó từ hóa và khó khử từ, nên ngược lại với vật liệu từ mềm, nó có lực kháng từ cao.
Một thanh sắt mềm và một thanh thép đều có cuộn dây quấn quanh. Cả hai thanh ban đầu đều không bị nhiễm từ. Các cuộn dây được gắn vào mạch điện như sau:
Kéo thả các cụm từ sau vào chỗ trống thích hợp:
Khi công tắc đóng thì cả lõi sắt mềm và cả thép đều bị _______. Khi mở công tắc thì thanh sắt mềm sẽ _______ và thanh thép sẽ _______.
Một học sinh thực hiện tạo ra một cuộn dây điện từ. Ban đầu, số vòng dây quấn là a (vòng ). Sau đó, học sinh quấn thêm một số lượng vòng dây. Kết luận nào sau đây về cường độ từ trường của cuộn dây.
