Câu hỏi:

18/01/2025 2

Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Điện lượng (nghìn mAh)

$\left[ {0,9;0,95} \right)$

$\left[ {0,95;1,0} \right)$

$\left[ {1,0;1,05} \right)$

$\left[ {1,05;1,1} \right)$

$\left[ {1,1;1,15} \right]$

Số viên pin

10

20

35

15

5

Hãy ước lượng tứ phân vị của mẫu số liệu ghép nhóm trên.

A. \[{{\rm{Q}}_{\rm{1}}}{\rm{ = 0,58; }}{{\rm{Q}}_{\rm{2}}}{\rm{ = 1,02; }}{{\rm{Q}}_{\rm{3}}}{\rm{ = 1,048}}\]

B. \[{{\rm{Q}}_{\rm{1}}}{\rm{ = 0,98; }}{{\rm{Q}}_{\rm{2}}}{\rm{ = 1,02; }}{{\rm{Q}}_{\rm{3}}}{\rm{ = 1,248}}\]

C. \[{{\rm{Q}}_{\rm{1}}}{\rm{ = 0,98; }}{{\rm{Q}}_{\rm{2}}}{\rm{ = 1,22; }}{{\rm{Q}}_{\rm{3}}}{\rm{ = 1,048}}\]

D. \[{{\rm{Q}}_{\rm{1}}}{\rm{ = 0,98; }}{{\rm{Q}}_{\rm{2}}}{\rm{ = 1,02; }}{{\rm{Q}}_{\rm{3}}}{\rm{ = 1,048}}\]

Đáp án chính xác

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Gọi \[{{\rm{x}}_{\rm{1}}}{\rm{; }}{{\rm{x}}_{\rm{2}}}{\rm{; }}{{\rm{x}}_{\rm{3}}}{\rm{; \ldots ; }}{{\rm{x}}_{{\rm{85}}}}\] lần lượt là số viên pin theo thứ tự không gian.
Do \[{{\rm{x}}_{\rm{1}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{10}}}} \in \left[ {0,9;0,95} \right);{{\rm{x}}_{{\rm{11}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{30}}}} \in \left[ {0,95;1,0} \right);{{\rm{x}}_{{\rm{31}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{65}}}} \in \left[ {1,0;1,05} \right)\]\[{{\rm{x}}_{{\rm{66}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{80}}}} \in \left[ {1,05;1,1} \right);{{\rm{x}}_{{\rm{81}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{85}}}} \in \left[ {1,1;1,15} \right)\]

Tứ phân vị thứ hai của dãy số liệu là \[\frac{{\rm{1}}}{{\rm{2}}}\left( {{{\rm{x}}_{{\rm{42}}}}{\rm{ + }}{{\rm{x}}_{{\rm{43}}}}} \right)\]thuộc nhóm \[\left[ {1,0;1,05} \right)\] nên tứ phân vị thứ hai của mẫu số liệu là \[{{\rm{Q}}_{\rm{2}}}{\rm{ = 1,0 + }}\frac{{\frac{{{\rm{85}}}}{{\rm{2}}} - {\rm{30}}}}{{{\rm{35}}}}\left( {{\rm{1,05}} - {\rm{1,0}}} \right){\rm{ = 1,02}}\]

Tứ phân vị thứ nhất của dãy số liệu là \[\frac{{\rm{1}}}{{\rm{2}}}\left( {{{\rm{x}}_{{\rm{21}}}}{\rm{ + }}{{\rm{x}}_{{\rm{22}}}}} \right)\]thuộc nhóm \[\left[ {0,95;1,0} \right)\] nên tứ phân vị thứ nhất của mẫu số liệu là \[{{\rm{Q}}_{\rm{1}}}{\rm{ = 0,95 + }}\frac{{\frac{{{\rm{85}}}}{{\rm{4}}} - {\rm{10}}}}{{{\rm{20}}}}\left( {{\rm{1,0}} - {\rm{0,95}}} \right){\rm{ = 0,98}}\]

Tứ phân vị thứ ba của dãy số liệu là \[\frac{{\rm{1}}}{{\rm{2}}}\left( {{{\rm{x}}_{{\rm{63}}}}{\rm{ + }}{{\rm{x}}_{{\rm{64}}}}} \right)\]thuộc nhóm \[\left[ {1,0;1,05} \right)\] nên tứ phân vị thứ ba của mẫu số liệu là \[{{\rm{Q}}_{\rm{3}}}{\rm{ = 1,0 + }}\frac{{\frac{{{\rm{3}}{\rm{.85}}}}{{\rm{4}}} - {\rm{30}}}}{{{\rm{35}}}}\left( {{\rm{1,05}} - {\rm{1,0}}} \right){\rm{ = 1,048}}\]

Đáp án cần chọn là: D

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 11 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 11 ở bảng sau:

Số vỏ chai nhựa

$\left[ {11;15} \right)$

$\left[ {16;20} \right)$

$\left[ {21;25} \right)$

$\left[ {26;30} \right)$

$\left[ {31;35} \right)$

Số học sinh

53

82

48

39

18

Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.

Xem đáp án » 18/01/2025 4

Câu 2:

Do số lần gặp sự cố là số nguyên nên ta hiệu chỉnh lại như sau:

Số lần gặp sự cố

$\left[ {0,5;2,5} \right)$

$\left[ {2,5;4,5} \right)$

$\left[ {4,5;6,5} \right)$

$\left[ {6,5;8,5} \right)$

$\left[ {8,5;10,5} \right]$

Số xe

17

33

25

20

5

Gọi \[{{\rm{x}}_{\rm{1}}}{\rm{; }}{{\rm{x}}_{\rm{2}}}{\rm{; \ldots ; }}{{\rm{x}}_{{\rm{100}}}}\] là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có \[{{\rm{x}}_{\rm{1}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{17}}}} \in [0,5;2,5);{{\rm{x}}_{{\rm{18}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{50}}}} \in [2,5;4,5);{{\rm{x}}_{{\rm{51}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{75}}}} \in [4,5;6,5)\]

\[{{\rm{x}}_{{\rm{76}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{95}}}} \in [6,5;8,5);{{\rm{x}}_{{\rm{96}}}}{\rm{, \ldots , }}{{\rm{x}}_{{\rm{100}}}} \in [8,5;10,5)\]

Tứ phân vị thứ nhất của dãy số liệu \[{{\rm{x}}_{\rm{1}}}{\rm{; }}{{\rm{x}}_{\rm{2}}}{\rm{; \ldots ; }}{{\rm{x}}_{{\rm{100}}}}\] là \[\frac{{\rm{1}}}{{\rm{2}}}\left( {{{\rm{x}}_{{\rm{25}}}}{\rm{ + }}{{\rm{x}}_{{\rm{26}}}}} \right)\]. Do x₂₅ và x₂₆ thuộc nhóm \[[2,5;4,5)\]nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

\[{{\rm{Q}}_{\rm{1}}}{\rm{ = }}2,5 + \frac{{\frac{{1.100}}{4} - 17}}{{33}} \cdot (4,5 - 2,5)\,\,{\rm{ = }}\frac{{197}}{{66}} \approx 2,98.\]

Đáp án cần chọn là: D

Xem đáp án » 18/01/2025 4

Câu 3:

Tổng lượng mưa trong tháng 8 đo được tại một trạm quan trắc đặt tại Vũng Tàu từ năm 2002 đến năm 2020 được ghi lại như dưới đây (đơn vị: mm):

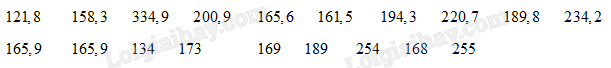
(Nguồn: Tổng cục Thống kê)

Hoàn thiện bảng tần số ghép nhóm theo mẫu sau và tìm tứ phân vị thứ hai của mẫu số liệu góp nhóm đó

Tổng lượng mưa trong tháng 8 (mm)

$\left[ {120;175} \right)$

$\left[ {175;230} \right)$

$\left[ {230;285} \right)$

$\left[ {285;340} \right)$

Số năm

x

y

z

t

Xem đáp án » 18/01/2025 3

Câu 4:

Kết quả khảo sát cân nặng của 25 quả cam ở lô hàng B được cho ở bảng sau:

Cân nặng (g)

$\left[ {150;155} \right)$

$\left[ {155;160} \right)$

$\left[ {160;165} \right)$

$\left[ {165;170} \right)$

$\left[ {170;175} \right)$

Số quả cam ở lô hàng A

1

3

7

10

4

Nhóm chứa mốt là nhóm nào

Xem đáp án » 18/01/2025 3

Câu 5:

Cân nặng của 28 học sinh nam lớp 11 được cho như sau:

Số trung bình của mẫu số liệu ghép nhóm trên xấp xỉ bằng

Xem đáp án » 18/01/2025 3

Câu 6:

Số khách hàng nam mua bảo hiểm ở từng độ tuổi được thống kê như sau:

Độ tuổi

$\left[ {20;30} \right)$

$\left[ {30;40} \right)$

$\left[ {40;50} \right)$

$\left[ {50;60} \right)$

$\left[ {60;70} \right)$

Số khách hàng nam

4

6

10

7

3

Hãy sử dụng dữ liệu ở trên để tư vấn cho đại lí bảo hiểm xác định khách hàng nam ở tuổi nào hay mua bảo hiểm nhất.

Xem đáp án » 18/01/2025 3

Câu 7:

Kết quả khảo sát cân nặng của 25 quả cam ở lô hàng A được cho ở bảng sau:

Cân nặng (g)

$\left[ {150;155} \right)$

$\left[ {155;160} \right)$

$\left[ {160;165} \right)$

$\left[ {165;170} \right)$

$\left[ {170;175} \right)$

Số quả cam ở lô hàng A

2

6

12

4

1

Cân nặng trung bình của mỗi quả cam ở lô hàng A xấp xỉ bằng

Xem đáp án » 18/01/2025 3

Câu 8:

Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):

Lương tháng (triệu đồng)

\[\left[ {6;8} \right)\]

\[\left[ {8;10} \right)\]

\[\left[ {10;12} \right)\]

\[\left[ {12;14} \right)\]

Số nhân viên

3

6

8

7

Tìm tứ phân vị của dãy số liệu trên.

Xem đáp án » 18/01/2025 3

Câu 9:

Trong tuẫn lễ bảo vệ môi trường, các học sinh khối 11 tiến hành thu nhặt vỏ chai nhựa để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ chai của học sinh khối 11 ở bảng sau:

Số vỏ chai nhựa

$\left[ {11;15} \right)$

$\left[ {16;20} \right)$

$\left[ {21;25} \right)$

$\left[ {26;30} \right)$

$\left[ {31;35} \right)$

Số học sinh

53

82

48

39

18

Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.

Xem đáp án » 18/01/2025 3

Câu 10:

Kết quả khảo sát cân nặng của 25 quả bơ ở một lô hàng cho trong bảng sau:

Cân nặng (g)

$\left[ {150;155} \right)$

$\left[ {155;160} \right)$

$\left[ {160;165} \right)$

$\left[ {165;170} \right)$

$\left[ {170;175} \right)$

Số quả bơ

1

7

12

3

2

Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

Xem đáp án » 18/01/2025 3

Câu 11:

Bảng 13 cho ta bảng tần số ghép nhóm số liệu thống kê cân nặng của 40 học sinh lớp 11A trong một trường trung học phổ thông (đơn vị: kilôgam).

Nhóm

Tần số

$\left[ {30;40} \right)$

2

$\left[ {40;50} \right)$

10

$\left[ {50;60} \right)$

16

$\left[ {60;70} \right)$

8

$\left[ {70;80} \right)$

2

$\left[ {80;90} \right)$

2

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép số trên.

Xem đáp án » 18/01/2025 2

Câu 12:

Cân nặng của lợn con giống A và giống B được thống kê như bảng sau:

Cân nặng (kg)

$\left[ {1,0;1,1} \right)$

$\left[ {1,1;1,2} \right)$

$\left[ {1,2;1,3} \right)$

$\left[ {1,3;1,4} \right)$

Số con giống A

8

28

32

17

Số con giống B

13

14

24

14

Hãy ước lượng trung vị và tứ phân vị thứ nhất của cân nặng lợn con mới sinh giống

A và của cân nặng lợn con mới sinh giống B.

Xem đáp án » 18/01/2025 2

Câu 13:

Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Doanh thu

$\left[ {5;7} \right)$

$\left[ {7;9} \right)$

$\left[ {9;11} \right)$

$\left[ {11;13} \right)$

$\left[ {13;15} \right)$

Số ngày

2

7

7

3

1

Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?

Xem đáp án » 18/01/2025 2

Câu 14:

Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:

Nhóm

Nhóm 1

Nhóm 2

…

Nhóm k

Giá trị đại diện

_c₁

_c₂

…

_{c_k}

Tần số

_n₁

_n₂

…

_{n_k}

Đặt ${n = n}_{1} {+ n}_{2} {+ …+ n}_{k}$

Số trung bình của mẫu số liệu ghép nhóm, kí hiệu $\bar{x}$ được tính theo công thức nào?

Xem đáp án » 18/01/2025 2

Câu 15:

Anh Văn ghi lại cự li 30 lần ném lao của mình ở bảng sau (đơn vị: mét) rồi Tổng hợp lại kết quả ném của anh Văn vào bảng tần số ghép nhóm theo mẫu sau:

Cự li (m)

$\left[ {69,2;70} \right)$

$\left[ {70;70,8} \right)$

$\left[ {70,8;71,6} \right)$

$\left[ {71,6;72,4} \right)$

$72,4;73,2$

Số lần

4

2

9

10

5

Khả năng anh Văn ném được khoảng bao nhiêu mét là cao nhất?

Xem đáp án » 18/01/2025 2

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản

7 đề 42315 lượt thi Thi thử
93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải

5 đề 29786 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn nâng cao

4 đề 25341 lượt thi Thi thử
75 câu trắc nghiệm Giới hạn cơ bản

4 đề 24507 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao

6 đề 23273 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác cơ bản

5 đề 21413 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm cơ bản

6 đề 19147 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác nâng cao

6 đề 18940 lượt thi Thi thử
Trắc nghiệm Hàm số lượng giác có đáp án

2 đề 16884 lượt thi Thi thử
299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết

11 đề 14028 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Tổng lượng mưa trong tháng 8 (mm)	\(\left[ {120;175} \right)\)	\(\left[ {175;230} \right)\)	\(\left[ {230;285} \right)\)	\(\left[ {285;340} \right)\)
Số năm	x	y	z	t

Cân nặng (g)	\(\left[ {150;155} \right)\)	\(\left[ {155;160} \right)\)	\(\left[ {160;165} \right)\)	\(\left[ {165;170} \right)\)	\(\left[ {170;175} \right)\)
Số quả cam ở lô hàng A	1	3	7	10	4

Độ tuổi	\(\left[ {20;30} \right)\)	\(\left[ {30;40} \right)\)	\(\left[ {40;50} \right)\)	\(\left[ {50;60} \right)\)	\(\left[ {60;70} \right)\)
Số khách hàng nam	4	6	10	7	3

Cân nặng (g)	\(\left[ {150;155} \right)\)	\(\left[ {155;160} \right)\)	\(\left[ {160;165} \right)\)	\(\left[ {165;170} \right)\)	\(\left[ {170;175} \right)\)
Số quả cam ở lô hàng A	2	6	12	4	1

Cân nặng (g)	\(\left[ {150;155} \right)\)	\(\left[ {155;160} \right)\)	\(\left[ {160;165} \right)\)	\(\left[ {165;170} \right)\)	\(\left[ {170;175} \right)\)
Số quả bơ	1	7	12	3	2

Điện lượng (nghìn mAh)	\(\left[ {0,9;0,95} \right)\)	\(\left[ {0,95;1,0} \right)\)	\(\left[ {1,0;1,05} \right)\)	\(\left[ {1,05;1,1} \right)\)	\(\left[ {1,1;1,15} \right]\)
Số viên pin	10	20	35	15	5

Số vỏ chai nhựa	\(\left[ {11;15} \right)\)	\(\left[ {16;20} \right)\)	\(\left[ {21;25} \right)\)	\(\left[ {26;30} \right)\)	\(\left[ {31;35} \right)\)
Số học sinh	53	82	48	39	18

Số lần gặp sự cố	\(\left[ {0,5;2,5} \right)\)	\(\left[ {2,5;4,5} \right)\)	\(\left[ {4,5;6,5} \right)\)	\(\left[ {6,5;8,5} \right)\)	\(\left[ {8,5;10,5} \right]\)
Số xe	17	33	25	20	5

Lương tháng (triệu đồng)	\[\left[ {6;8} \right)\]	\[\left[ {8;10} \right)\]	\[\left[ {10;12} \right)\]	\[\left[ {12;14} \right)\]
Số nhân viên	3	6	8	7

Nhóm	Tần số
\(\left[ {30;40} \right)\)	2
\(\left[ {40;50} \right)\)	10
\(\left[ {50;60} \right)\)	16
\(\left[ {60;70} \right)\)	8
\(\left[ {70;80} \right)\)	2
\(\left[ {80;90} \right)\)	2

Cân nặng (kg)	\(\left[ {1,0;1,1} \right)\)	\(\left[ {1,1;1,2} \right)\)	\(\left[ {1,2;1,3} \right)\)	\(\left[ {1,3;1,4} \right)\)
Số con giống A	8	28	32	17
Số con giống B	13	14	24	14

Doanh thu	\(\left[ {5;7} \right)\)	\(\left[ {7;9} \right)\)	\(\left[ {9;11} \right)\)	\(\left[ {11;13} \right)\)	\(\left[ {13;15} \right)\)
Số ngày	2	7	7	3	1

Nhóm	Nhóm 1	Nhóm 2	…	Nhóm k
Giá trị đại diện	_c₁	_c₂	…	_{c_k}
Tần số	_n₁	_n₂	…	_{n_k}

Cự li (m)	\(\left[ {69,2;70} \right)\)	\(\left[ {70;70,8} \right)\)	\(\left[ {70,8;71,6} \right)\)	\(\left[ {71,6;72,4} \right)\)	\(72,4;73,2\)
Số lần	4	2	9	10	5