Cho số phức z thỏa mãn .
Tính GTLN của
A. maxP=
B. maxP=
C. maxP=
D. maxP=
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Cho số phức ![]() ,S(x;y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
,S(x;y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
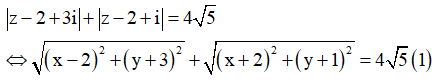
Lấy các điểm A(2;-3),B(-2;-1)
Phương trình ![]()
![]() Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;-3),B(-2;-1) và có độ dài trục lớn là
Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2;-3),B(-2;-1) và có độ dài trục lớn là ![]()
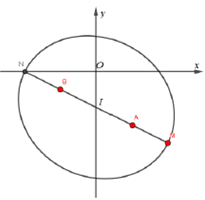
Lấy M(4;-4).
Dễ dàng kiểm tra được 
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB
![]() I(0;-2) ,N là điểm đối xứng của M qua I.
I(0;-2) ,N là điểm đối xứng của M qua I.
Khi đó, với mọi điểm ![]()
![]() khi và chỉ khi S trùng N
khi và chỉ khi S trùng N
![]() khi và chỉ khi SN(-4;0)
khi và chỉ khi SN(-4;0)
![]() z=-4
z=-4
Cho hai số phức thỏa mãn .
Gọi M, N là các điểm biểu diễn cho và .
Biết . Tính ?
Tìm phần thực của số phức biết rằng là hai nghiệm phức của phương trình
Gọi và là hai nghiệm phức của phương trình .
Giá trị của biểu thức bằng
Kí hiệu là hai nghiệm phức của phương trình
Giá trị của biểu thức P= bằng: