Cho số phức z thỏa mãn điều kiện .
Giá trị lớn nhất của là
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức ![]() , có điểm biểu diễn là M(x;y)
, có điểm biểu diễn là M(x;y)

![]() M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
Tìm giá trị lớn nhất của ![]() tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:
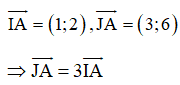
điểm A nằm trên trục lớn của elip.
![]() AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
![]() S(0;-1)
S(0;-1)
Độ dài đoạn AB=SA+SB
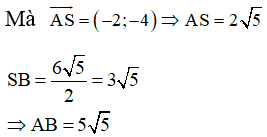
Vậy ![]()
Cho hai số phức thỏa mãn .
Gọi M, N là các điểm biểu diễn cho và .
Biết . Tính ?
Tìm phần thực của số phức biết rằng là hai nghiệm phức của phương trình
Gọi và là hai nghiệm phức của phương trình .
Giá trị của biểu thức bằng
Kí hiệu là hai nghiệm phức của phương trình
Giá trị của biểu thức P= bằng: