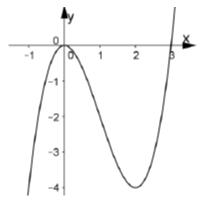
Cho hàm số y = ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 5
D. 4
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có thể vẽ đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| theo ba bước sau:
Dựa vào đồ thị ta thấy hàm số có 5 cực trị
Chọn C.
Cho phương trình x3 - 3x2 + 1 - m = 0 (1). Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa x1 < 1 < x2 < x3 khi
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
Tìm m để đồ thị hàm số y = x3+mx+2 cắt trục hoành tại một điểm duy nhất.
Cho hàm số có đồ thị là (C) . Tìm m để đường thẳng d: y=2x-1 cắt đồ thị (C) tại hai điểm phân biệt A; B sao cho AB =
Cho hàm số y=x3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
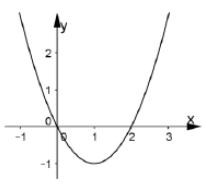
Cho hàm số y= f(x) =ax3+ bx2+cx+d có đạo hàm là hàm số y= f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
Tìm tất cả các giá trị thực của tham số m sao cho hàm số nghịch biến trên một đoạn có độ dài là 3?
Với giá trị nào của tham số m thì (C): y=x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
Tìm tất các giá trị thực của tham số m để hàm số đạt cực trị tại thỏa mãn -2<
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y= 2sin8 x+ cos42x. Khi đó M + m bằng
Hàm số y = x8 + (x4 – 1) 2 + 5 đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2] lần lượt tại hai điểm có hoành độ x1; x2. Khi đó tích x1.x2 có giá trị bằng:
Cho phương trình =1 có nghiệm duy nhất có dạng b/a, trong đó a; b là số tự nhiên, b/a là phân số tối giản. Hãy tính giá trị của a+ 2b