200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
23245 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
Tìm tất các giá trị thực của tham số m để hàm số đạt cực trị tại thỏa mãn -2<
 Xem đáp án
Xem đáp án
+ Ta có: y' = x2 + 2(m+3)x + 4(m+3)
Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x1; x2 thỏa mãn: -2 < x1< x2
Chọn C
Câu 2:
Tìm các giá trị của tham số m để hàm số:
đạt cực trị tại
 Xem đáp án
Xem đáp án
Ta có: y' =
Yêu cầu của bài toán tương đương y’ = 0 có hai nghiệm phân biệt
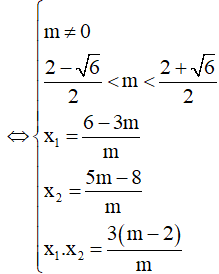
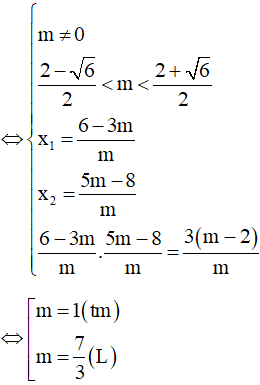
Chọn D.
Câu 3:
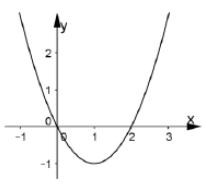
Cho hàm số y= f(x) =ax3+ bx2+cx+d có đạo hàm là hàm số y= f’ (x) với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x) cắt trục tung tại điểm có tung độ là bao nhiêu?
 Xem đáp án
Xem đáp án
+ Ta có đạo hàm f’(x) = 3ax2+ 2bx+c .
+ Dựa vào đồ thị hàm số y = f’(x) ta thấy đồ thị hàm số đi qua các điểm (0; 0); (1; -1); (2; 0) nên a = 1/3; b = -1; c = 0.
Do vậy hàm số cần tìm có dạng y = 1/3 x3-x2+ d .
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x = 0 hoặc x = 2.
+ Vì đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x = 2 nghĩa là:
f(2) = 0 hay 8/3 - 4 + d= 0 nên d = 4/3
Chọn D.
Câu 4:
Giá trị lớn nhất của hàm số bằng
 Xem đáp án
Xem đáp án
Chọn D.
+) Điều kiện: -4 ≤ x ≤ 4.
Ta thấy hàm số f(x) liên tục trên đoạn [ -4; 4]
đặt t =
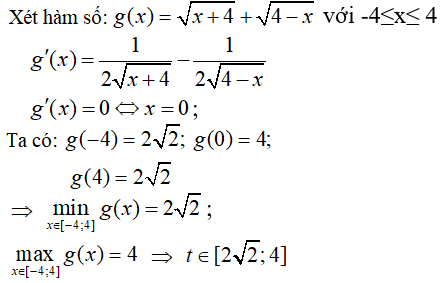
Ta có:
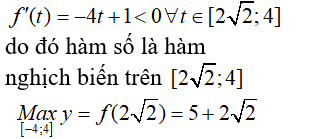
Câu 5:
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
 Xem đáp án
Xem đáp án
2x3-3x2+1 =x-1 hay 2x3-3x2-x+2=0
Khi đó ta có A(1 ; 0) ; B( x1 ; x1-1) và C( x2 ; x2-1) ( x1 ; x2 là nghiệm của (1))
Ta có , suy ra
![]()
Chọn B.
Câu 6:
Giá trị nhỏ nhất của hàm số y= 2sin4x+ cos2x+ 3 bằng
 Xem đáp án
Xem đáp án
Ta có 2sin4x + cos2x + 3 = 2sin4x - sin2x + 4.
Đặt t = sin2x; 0 ≤ t = sin2 x ≤1
Xét hàm số: f( t) = 2t4 - t2 + 4 liên tục trên đoạn [0;1]
Có đạo hàm f’(t) = 8t3 - 2t = 2t( 4t2 - 1)
Trên khoảng (0;1) phương trình f’(t) =0 khi và chỉ khi t = 1/2
Ta có: f(0) = 4; f(1/ 2) = 31/ 8 và f(1) = 5.
Vậy
Chọn D.
Câu 7:
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y= 2sin8 x+ cos42x. Khi đó M + m bằng
 Xem đáp án
Xem đáp án
Chọn C.
Do nên ta có
Đặt t = cos2x;
Bài toán trở thành tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
G(t)=1/8.
ta có:
Lại có: g(1)=1; g(-1)=3; g(1/3)=1/27
Vậy m = 1/27; M=3
nên M+m=3+1/27=
Câu 8:
Tìm m để đồ thị hàm số y = x3+mx+2 cắt trục hoành tại một điểm duy nhất.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là
Vì x=0 không là nghiệm của phương trình, nên phương trình tương đương với
. Xét hàm số:
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy đồ thị cắt trục hoành tại một điểm duy nhất khi và chỉ khi m> -3.
Vậy m>-3 thỏa yêu cầu bài toán.
Chọn C.
Câu 9:
Hàm số có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:
 Xem đáp án
Xem đáp án
TXĐ: D= [ -3; 1].
Đặt:
Khi đó phương trình trở thành:
Do đó hàm số đồng biến trên D.
Chọn B.
Câu 10:
Cho f(x) =. Số cực trị của hàm số y = |f(x)-1| là:
 Xem đáp án
Xem đáp án
Ta có:
Do pt có 3 điểm cực trị ( vì ab< 0) nên phương trình f’ ( x) =0 có 3 nghiệm phân biệt.
Do đó (*) có 3 nghiệm phân biệt.
Chọn C.
Câu 11:
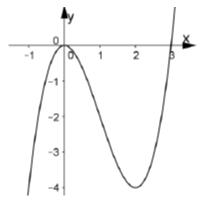
Cho hàm số y = ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Ta có thể vẽ đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| theo ba bước sau:
Dựa vào đồ thị ta thấy hàm số có 5 cực trị
Chọn C.
Câu 12:
Hàm số đạt giá trị lớn nhất, giá trị nhỏ nhất tại điểm có hoành độ là:
 Xem đáp án
Xem đáp án
TXD: D=[-2;2].
Đặt:
Khi đó hàm số trở thành:
và có đạo hàm trên D
=> hàm số đồng biến với mọi
Do đó; min y = f(2)=2
Chọn A
Câu 13:
Cho hàm số có đồ thị là (C) . Tìm m để đường thẳng d: y=2x-1 cắt đồ thị (C) tại hai điểm phân biệt A; B sao cho AB =
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
Điều kiện: x Khi đó
(1) Suy ra: mx-1=(2x-1) (x+2) hay 2x2-(m-3)x-1=0 (2)
Đường thẳng d cắt (C) tại hai điểm phân biệt A; B khi và chỉ khi (1) có hai nghiệm phân biệt suy ra (2) có hai nghiệm phân biệt khác -2
Đặt A( x1; 2x1-1); B( x2; 2x2-1) với x1; x2 là hai nghiệm của phương trình (2).
Theo định lý Viet ta có
thỏa (*).
Vậy giá trị m cần tìm là m =3.
Câu 14:
Hàm số y = x8 + (x4 – 1) 2 + 5 đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2] lần lượt tại hai điểm có hoành độ x1; x2. Khi đó tích x1.x2 có giá trị bằng:
 Xem đáp án
Xem đáp án
Đặt t= x4- 1( -1≤ t≤ 15).
Khi đó hàm số trở thành: y= ( t+1) 2+ t2+ 5=2t2+ 2t+6
Đạo hàm y’ = 4t+ 2> 0 mọi x thòa mãn 0≤ x≤ 2
Hàm số đồng biến trên đoạn [0; 2].
Hàm số đạt giá trị lớn nhất tại x= 2 tức là t= 15, hàm số đạt giá trị nhỏ nhất tại x= 0 hay t=1
Chọn D.
Câu 15:
Cho phương trình =1 có nghiệm duy nhất có dạng b/a, trong đó a; b là số tự nhiên, b/a là phân số tối giản. Hãy tính giá trị của a+ 2b
 Xem đáp án
Xem đáp án
Điều kiện:
Đạo hàm
Suy ra hàm số đồng biến trên
Do đó : phương trình
Chọn B.
Câu 16:
Cho phương trình x3 - 3x2 + 1 - m = 0 (1). Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa x1 < 1 < x2 < x3 khi
 Xem đáp án
Xem đáp án
Ta có x3 - 3x2 + 1 - m = 0 (1) là phương trình hoành độ giao điểm giữa hai đồ thị hàm số y = x3-3x2+1 và y = m (là đường thẳng song song hoặc trùng với Ox).
Xét y = x3-3x2+1 .
Tính y’ = 3x2- 6x
Ta có
Ta có x = 1 thì y = -1
Số nghiệm của phương trình chính là số giao điểm của đồ thị y = x3-3x2+1 và đường thẳng y = m .
Do đó, yêu cầu bài toán khi và chỉ khi -3 < m < -1
Chọn C.
Câu 17:
Cho phương trình:
Tính tổng các nghiệm cùa phương trình là :
 Xem đáp án
Xem đáp án
Điều kiện. x≥1/3
Ta có:
Xét hàm số f(t) = 2t3 + t2 + 1 liên tục trên R.
Ta có: đạo hàm f’(t) = 6t2 + 2t > 0 với t > 0 .
Do đó: hàm số f(t) đồng biến trên (0; +∞).
Tổng các nghiệm là 3.
Chọn C.
Câu 18:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số nghịch biến trên một đoạn có độ dài là 3?
 Xem đáp án
Xem đáp án
+ Đạo hàm y’ = x2- mx+ 2m
Hàm số nghịch biến trên một đoạn có độ dài là 3 khi và chi khi phương trình y’ =0 có 2 nghiệm x1; x2 ( chú ý hệ số a= 1> 0) thỏa mãn:
Chọn A.
Câu 19:
Với giá trị nào của tham số m thì (C): y=x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của đồ thị (C) và trục Ox:
x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1)=0
hay (x-2) (x2-(3m+1) x+2m2+2m)=0
Chọn A.
Câu 20:
Cho hàm số y=x3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
 Xem đáp án
Xem đáp án
Phương trình đường thẳng d: y = k(x - 1) + 2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
x3 - 3x2 + 4 = k(x - 1) + 2.
Hay x3 - 3x2 - kx + k + 2 = 0 (1)
( C) cắt d tại ba điểm phân biệt khi và chỉ khi phương trình (*) có hai nghiệm phân biệt x1; x2 khác 1
Hơn nữa theo Viet ta có
nên I là trung điểm AB.
Vậy chọn k > -3, hay k ∈ (-3; +∞). Do đó có vô số giá trị k nguyên thỏa mãn yêu cầu bài toán.
Chọn D.
