200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P6)
-
23196 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số có đồ thị là (C) . Gọi I là giao điểm hai tiệm cận của (C) . tồn tại điểm M( a; b) với; a; b nguyên dương thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI. Khi đó b-a= ?
 Xem đáp án
Xem đáp án
+Đồ thị hàm số đã cho có TCĐ là x= 1 và TCN là y= 2; giao điểm của hai tiệm cận là
I (1; 2) .
Lấy điểm
+ Phương trình tiếp tuyến của (C ) tại M là
+ Phương trình đường thẳng MI là
+ Tiếp tuyến tại M vuông góc với MI nên ta có
Vì yêu cầu hoành độ và tung độ của M nguyên dương nên điểm cần tìm là M( 2; 3).
Chọn D.
Câu 2:
Cho hàm số có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
+ Phương trình hoành độ giao điểm của d và (C) là
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.
Câu 3:
Cho hàm số .Viết phương trình tiếp tuyến của đồ thị hàm số đã cho, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB cân tại gốc tọa độ.
 Xem đáp án
Xem đáp án
+ Gọi M(a; b) là toạ độ của tiếp điểm
Đạo hàm .
+ Do tam giác OAB cân tại O nên tiếp tuyến ∆ song song với đường thẳng y= -x (vì tiếp tuyến có hệ số góc âm).
Nghĩa là
-Với a= -1; b= 1 phương trình ∆: y- 1= -( x+ 1) hay y= -x ( loại) .
-Với a= -2; b= 0 thì ∆ : y- 0= -( x+ 2) hay y=-x-2 (nhận).
Vậy phương trình tiếp tuyến cần tìm là y= -x- 2.
Chọn D.
Câu 4:
Cho hàm số . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
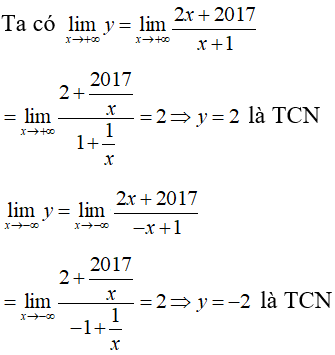
Suy ra đồ thị hàm số có 2TCN là y= 2 và y= -2 .
Chọn B.
Câu 5:
Biết đường thẳng y= (3m-1) x+ 6m+3 cắt đồ thị hàm số y= x3-3x2+ 1 tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
PT hoành độ giao điểm là
(3m-1) x+ 6m+ 3 = x3-3x2+ 1 hay x3-3x2 – (3m-1) x-6m-2=0 ( *)
Giả sử A( x1; y1) ; B( x2; y2); B( x3; y3) lần lượt là giao điểm của (C) và (d)
Vì B cách đều hai điểm A và C nên B là trung điểm của AC
Suy ra x1+ x3= 2x2
Thay x2 = 1vào , ta có
Vậy -1< m< 0
Chọn C.
Câu 6:
Số nguyên nhỏ nhất của tham số để PT có nghiệm là
 Xem đáp án
Xem đáp án
Điều kiện x≥ 0.
Dễ thấy x = 0 không là nghiệm của phương trình.
Xét x> 0 , chia cả 2 vế của phương trình cho x ta được
Đặt , khi đó phương trình ( *) trở thành: t2- (m - 1)t + m + 2 = 0
Vì t ≥ 2 nên t - 1 ≠ 0 nên phương trình
Xét hàm số
Khi đó, để phương trình m =f( t) có nghiệm
Chọn C.
Câu 7:
Để chặn đường hành lang hình chữ L người ta dung một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ bên). Biết rằng a = 24 và b = 3, hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?

 Xem đáp án
Xem đáp án
Theo bài ra, thanh sào sẽ đi qua các điểm B, M , C (hình vẽ dưới)
Suy ra độ dài thanh sào là
Đặt ,do đó
Yêu cầu bài toán
Ta có
Suy ra . Vậy độ dài tối thiểu của thanh sào là
Chọn C.
Câu 8:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số y= x3+ x2+ mx-1 nằm bên phải trục tung. Tìm số phần tử nguyên của tập hợp
 Xem đáp án
Xem đáp án
Ta có đạo hàm y’ = 3x2+ 2x+ m.
Hàm số có cực trị khi
Do hàm số có a=1>0
Yêu cầu bài toán trở thành phương trình y’ = 0 có ít nhất 1 nghiệm dương
Do là giá trị cần tìm.
Vậy
Mà m nguyên nên chọn -4; -3; -2; -1. Có 4 giá trị thỏa mãn.
Chọn D.
Câu 9:
Cho hàm số . Tìm tất cả các giá trị thực của tham số m sao cho phương trình có đúng 3 nghiêm phân biệt.
 Xem đáp án
Xem đáp án
Phương trình
Dựa vào đồ thị hàm số suy ra đồ thị hàm số
Số nghiệm của phương trình (*) là số giao điểm của (C) và đường thẳng
Vậy để (*) có 3 nghiệm phân biệt
( học sinh tự vẽ đồ thị hàm số (C) ).
Chọn A.
Câu 10:
Tìm tất cả các giá trị thực của m để đường thẳng y= x+ m-1 cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của ( C) và d là
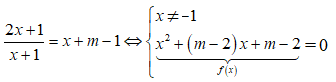
Để (C) cắt (d) tại hai điểm phân biệt khi và chỉ khi f( x) = 0 có hai nghiệm phân biệt
Gọi A(x1; y1) ; B(x2; y2) là giao điểm của (C) và d
Theo hệ thức Viet, ta được
mà
Chọn D.
Câu 11:
Cho hàm số có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
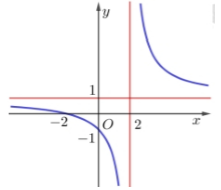
 Xem đáp án
Xem đáp án
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số có TCĐ và TCN là
Đồ thị hàm số đi qua điểm có tọa độ ( -2; 0) nên a= -2
Suy ra A= a+ b+ c= -2+ 1+ ( -2) = -3
Chọn B.
Câu 12:
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
Giả sử phương trình đã cho có 3 nghiệm
Khi đó
Suy ra
Xét hàm số:
Chọn D.
Câu 13:
Cho hàm số y= f( x) liên tục trên R Đồ thị của hàm số y= f’ (x) như hình bên. Đặt g(x) = 2f(x)-(x+ 1) 2 . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
+ Với x< - 3 ta có: f’ (x)< x + 1 suy ra hàm số nghịch biến trên khoảng ( -∞; -3)
+ Xét hàm số g( x) ; ta cần so sánh g(-3) và g( 3)
Ta có g(x) = 2f(x) – ( x + 1) 2 nên g’(x) = 2f’(x) - 2(x + 1)
Phương trình (Dựa vào đồ thị hàm số y= f’ (x)) .
Bảng xét dấu của g’(x)
Dựa vào bảng xét dấu, ta được
Dựa vào hình vẽ lại có
Do đó g( 1) – g( -3) > g( 1) – g( 3) hay g( 3) > g( -3) .
Suy ra GTNN của hàm số trên đoạn [- 3; 3] là g( -3) .
Chọn B.
Câu 14:
Cho hàm số có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a> 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM.
Giá trị a+ b bằng
 Xem đáp án
Xem đáp án
Hệ số góc của đường thẳng IM là:
Mặt khác tiếp tuyến tại M có hệ số góc
Giả thiết bài toán
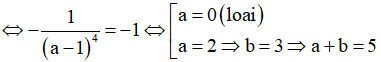
Chọn C.
Câu 15:
Có bao nhiêu giá trị nguyên dương của m để hàm số y= 3x+ m(sinx+ cosx+m) đồng biến trên R ?
 Xem đáp án
Xem đáp án
Đạo hàm :
Hàm số đồng biến trên R khi y’ ≥ 0 với mọi x
Vậy có 2 giá trị nguyên dương của m thỏa mãn đầu bài.
Chọn D.
Câu 16:
Cho hàm số M và N là hai điểm thuộc đồ thị hàm số sao cho tiếp tuyến của đồ thị hàm số tại M và N song song với nhau. Khẳng định nào sau đây là SAI?
 Xem đáp án
Xem đáp án
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau nên hệ số góc của chúng bằng nhau g=hay
Gọi là hai điểm thuộc đồ thị hàm số.
Tiếp tuyến của đồ thị hàm số tại M và N song song với nhau
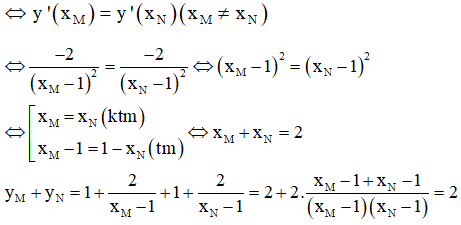
Gọi I là trung điểm của MN ta có: I (1; 1)
Dễ thấy đồ thị hàm số có TCN là y = 1và tiệm cận đứng x = 1 nên I (1; 1) là giao điểm của hai đường tiệm cận => C đúng.
TCN y = 1 và tiệm cận đứng x = 1 rõ ràng đi qua trung điểm I của đoạn MN => B, D đúng.
Chọn A.
Câu 17:
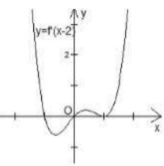
gCho hàm số y= f( x) có đạo hàm liên tục trên R, hàm số y= f’ (x-2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y= f( x) là :
 Xem đáp án
Xem đáp án
Ta có: f' (x - 2) = f' (x).(x-2)' = f'(x)
Do đó; đồ thị hàm số y= f’ (x) có hình dạng tương tự như trên.
Xét phương trình f'(x-2) = 0 có 3 nghiệm x = -1; x = 0; x = 1
nhưng f'(x - 2) chỉ đổi dấu qua 2 nghiệm x = -1 và x = 0 nên hàm số y= f( x-2) có 2 điểm cực trị.
Suy ra hàm số y = f(x) cũng có 2 điểm cực trị.
Chọn B.
Câu 18:
Giá trị của m để hàm số nghịch biến trên là
 Xem đáp án
Xem đáp án
Ta có:
Để hàm số nghịch biến trên khoảng
Mà
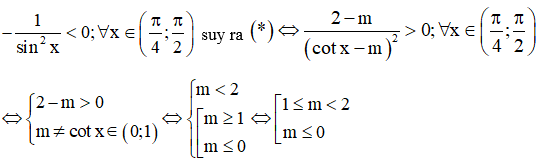
Vậy là giá trị cần tìm.
Chọn B.
Câu 19:
Cho hàm số y= f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a< b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
 Xem đáp án
Xem đáp án
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Ta có f’ (x) = -x2-1< 0 với a< x< b ; suy ra hàm số y= f( x) là hàm số nghịch biến trên [ a; b].
Mà a< b nên f(a) > f( b)
Vậy
Chọn C.
Câu 20:
Cho hàm số y= f( x) có đạo hàm Số điểm cực trị của hàm số là
 Xem đáp án
Xem đáp án
Do đó hàm số f(|x|) có 3 điểm cực trị tại x= 2; x= -2 và x= 0
Chọn B.
