Cho hàm số y= f( x) liên tục trên R Đồ thị của hàm số y= f’ (x) như hình bên. Đặt g(x) = 2f(x)-(x+ 1) 2 . Mệnh đề nào dưới đây đúng?
A.
B.
C.
D. Không tồn tại giá trị nhỏ nhất của g( x) trên [-3;3]
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
+ Với x< - 3 ta có: f’ (x)< x + 1 suy ra hàm số nghịch biến trên khoảng ( -∞; -3)
+ Xét hàm số g( x) ; ta cần so sánh g(-3) và g( 3)
Ta có g(x) = 2f(x) – ( x + 1) 2 nên g’(x) = 2f’(x) - 2(x + 1)
Phương trình (Dựa vào đồ thị hàm số y= f’ (x)) .
Bảng xét dấu của g’(x)
Dựa vào bảng xét dấu, ta được
Dựa vào hình vẽ lại có
Do đó g( 1) – g( -3) > g( 1) – g( 3) hay g( 3) > g( -3) .
Suy ra GTNN của hàm số trên đoạn [- 3; 3] là g( -3) .
Chọn B.
Cho hàm số có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
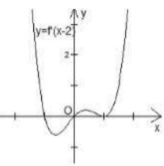
gCho hàm số y= f( x) có đạo hàm liên tục trên R, hàm số y= f’ (x-2) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số y= f( x) là :
Tìm tất cả các giá trị thực của m để đường thẳng y= x+ m-1 cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để điểm cực tiểu của đồ thị hàm số y= x3+ x2+ mx-1 nằm bên phải trục tung. Tìm số phần tử nguyên của tập hợp
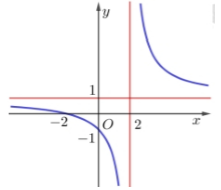
Cho hàm số có đồ thị là (C) . Gọi I là giao điểm hai tiệm cận của (C) . tồn tại điểm M( a; b) với; a; b nguyên dương thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI. Khi đó b-a= ?
Cho hàm số .Viết phương trình tiếp tuyến của đồ thị hàm số đã cho, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB cân tại gốc tọa độ.
Biết đường thẳng y= (3m-1) x+ 6m+3 cắt đồ thị hàm số y= x3-3x2+ 1 tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
Cho hàm số y= f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a< b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
Cho hàm số M và N là hai điểm thuộc đồ thị hàm số sao cho tiếp tuyến của đồ thị hàm số tại M và N song song với nhau. Khẳng định nào sau đây là SAI?
Cho hàm số có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
Cho hàm số . Tìm tất cả các giá trị thực của tham số m sao cho phương trình có đúng 3 nghiêm phân biệt.