20 câu hỏi trắc nghiệm thuộc 200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P10)

Câu 1:

Cho hàm số y = f(x) = $\frac{a x + b}{c x + d}$ ( a,b,c,d $\in ℝ$ , $\frac{- d}{c}$ $\neq$ 0) đồ thị hàm số y= f’(x) như hình vẽ.

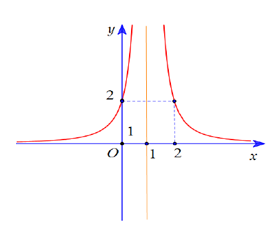
Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?

A. y = $\frac{x - 3}{x + 1}$

B. y = $\frac{x + 3}{x - 1}$

C. y = $\frac{x + 3}{x + 1}$

D. y = $\frac{x - 3}{x - 1}$

Xem đáp án

+ Ta có $y^{'} = f^{'} (x)$ = $\frac{a d - b c}{{(c x + d)}^{2}}$ . Từ đồ thị hàm số y= f’(x) ta thấy:

Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d

Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)

$\Rightarrow \frac{a d - b c}{{(2 c + d)}^{2}} = 2 \leftrightarrow a d - b c = 2$ $(2 c + d)^{2}$

Đồ thị hàm số y= f’(x) đi qua điểm (0;2)

$\Rightarrow \frac{a d - b c}{d^{2}} = 2 \leftrightarrow a d - b c = 2 d^{2}$

Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d

Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .

Ta chọn a=c= 1 ; b= -3 ; d= -1

$\Rightarrow y = \frac{x - 3}{x - 1}$

Chọn D.

Câu 2:

Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số $y = \frac{x}{|x - 1|}$ ?

A.

B.

C.

D.

Xem đáp án

Ta có y = $\frac{x}{|x - 1|} = \{\begin{cases} \frac{x}{x - 1} k h i x > 1 \\ - \frac{x}{x - 1} k h i x < 1 \end{cases}$

Do đó đồ thị hàm số $y = \frac{x}{|x - 1|}$ được suy từ đồ thị hàm số $y = \frac{x}{x - 1}$ bằng cách:

● Giữ nguyên phần đồ thị hàm số phía bên phải đường thẳng x = 1.

● Phần đồ thị hàm số

$y = \frac{x}{x - 1}$

phía bên trái đường thẳng x= 1 thì lấy đối xứng qua trục hoành.

Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số y = $\frac{x}{|x - 1|}$

Chọn B.

Câu 3:

Hàm số y= 2x³-9x²+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình $2 {|x|}^{3} - 9 x^{2} + 12 |x| + m = 0$ có sáu nghiệm phân biệt.

A.m< - 5

B. -5< m<- 4

C. 4< m< 5

D.m> -4

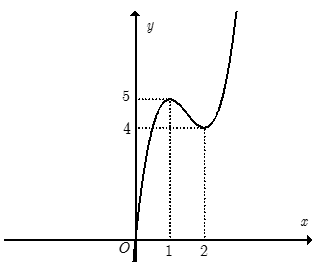
Xem đáp án

+Trước tiên từ đồ thị hàm số y= 2x³- 9x²+12x , ta suy ra đồ thị hàm số y= 2 ${|x|}^{3} - 9 x^{2} + 12 |x|$ như hình dưới đây:

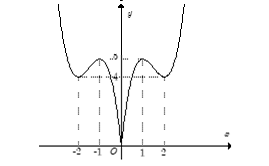
+ Phương trình $2 {|x|}^{3} - 9 x^{2} + 12 |x| + m = 0$ và đường thẳng y= -m

+ Dựa vào đồ thị hàm số y = $2 {|x|}^{3} - 9 x^{2} + 12 |x|$ , yêu cầu bài toán trở thành:

4< -m< 5 hay -5<m< -4.

Chọn B.

Câu 4:

Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình $|f (x)| = m$ có đúng hai nghiệm phân biệt.

A.0< m< 1 .

B. m> 5.

C.m= 1; m= 5

D.0< m< 1; m> 5

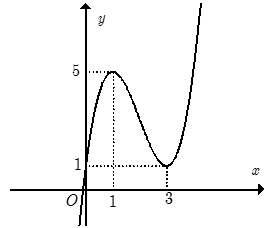
Xem đáp án

+ Ta có y = $|f (x)| = \{\begin{cases} f (x), f (x) \geq 0 \\ - f (x), f (x) < 0 \end{cases}$ . Từ đó suy ra cách vẽ đồ thị hàm số (C) như sau:

- Giữ nguyên đồ thị y= f (x) phía trên trục hoành.

- Lấy đối xứng phần đồ thị y= f(x) phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).

Kết hợp hai phần ta được đồ thị hàm số y = $|f (x)|$ như hình vẽ.

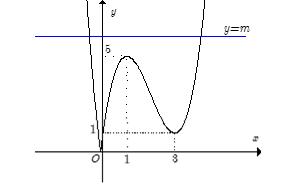
Phương trình $|f (x)| = m$ là phương trình hoành độ giao điểm của đồ thị hàm số y = $|f (x)|$ và đường thẳng

y= m (cùng phương với trục hoành).

Dựa vào đồ thị, ta có ycbt

Chọn D.

Câu 5:

Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình

2 $|f (x)|$ - m = 0 có đúng bốn nghiệm phân biệt.

A. 0< m< 8

B.m> 4

C.m< 0 ; m> 8

D. -2< m< 4

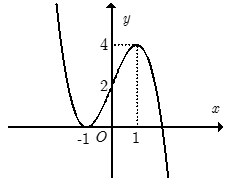
Xem đáp án

+ Trước tiên từ đồ thị hàm số y = f( x) , ta suy ra đồ thị hàm số y = |f(x)| như hình dưới đây:

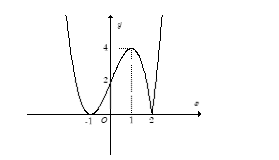
Phương trình 2|f(x)| - m = 0 hay |f(x)| = m/2 là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m/2.

Dựa vào đồ thị hàm số y = |f(x)|, ta có ycbt trở thành:

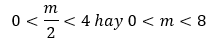
Chọn A.

Câu 6:

Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|) = -1/2 có bao nhiêu nghiệm?

A. 2.

B. 0.

C. 6.

D. 4.

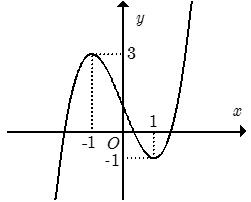
Xem đáp án

+ Trước tiên tịnh tiến đồ thị sang phải 2 đơn vị để được đồ thị hàm số y = f(x - 2) .

+ Tiếp theo giữ phần đồ thị phía bên phải đường thẳng x = 2, xóa bỏ phần đồ thị phía bên trái đường thẳng x = 2.

+ Cuối cùng lấy đối xứng phần đồ thị vừa giữ lại ở trên qua đường thẳng x= 2. Ta được toàn bộ phần đồ thị của hàm số

y = f(|x-2|) (hĩnh vẽ bên dưới)

Dựa vào đồ thị hàm số y = f(|x -2|) , ta thấy đường thẳng y= -1/2 cắt đồ thị hàm số y = f(|x-2|) tại 4 điểm phân biệt khi và chỉ khi phương trình f(|x-2|) = -1/2 có 4 nghiệm phân biệt.

Chọn D.

Câu 7:

Cho hàm số y= f(x )= ax³+ bx²+ cx+ d có bảng biến thiên như sau:

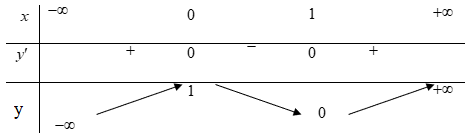
Khi đó |f(x)| = m có 4 nghiệm phân biệt $x_{1} < x_{2} < x_{3} < \frac{1}{2} < x_{4}$ khi và chỉ khi

A. ½< m< 1

B. 0< m

C. m> 1

D. m< 1/2

Xem đáp án

Ta có $\{\begin{cases} \begin{matrix} f (0) = 1 \\ f (1) = 0 \\ f^{'} (0) = 0 \end{matrix} \\ f^{'} (1) = 0 \end{cases}$

$\leftrightarrow \{\begin{cases} \begin{matrix} a = 2 \\ b = - 3 \\ c = 0 \end{matrix} \\ d = 1 \end{cases}$

, suy ra hàm số đã cho là : y= 2x³-3x²+ 1.

Ta thấy: f(x) = 0 $\leftrightarrow$ x = 0 hoặc x = -1/2

Bảng biến thiên của hàm số y = |f(x)| như sau:

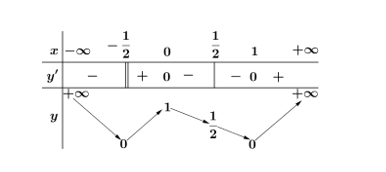
Dựa vào bảng biến thiên suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x₁< x₂< x₃< ½< x₄ khi và chỉ khi ½< m< 1.

Chọn A.

Câu 8:

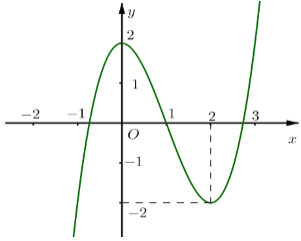
Cho hàm số f(x) = x³- 3x²+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình ${|x|}^{3} - 3 x^{2} + 2 = m$ có nhiều nghiệm thực nhất

A. m > -2

B. m > 0

C. -2 < m < 2.

D. m < 2.

Xem đáp án

+ Ta có hàm số g(x) = ${|x|}^{3} - 3 x^{2} + 2 = m$ là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng.

+ Khi x ≥ 0; g(x) = x³- 3x²+ 2

Do đó: đồ thị hàm số g(x) = $x^{3} - 3 x^{2} + 2$ có dạng như hình vẽ.

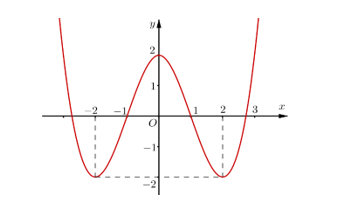
+ Dựa vào đồ thị suy ra phương trình ${|x|}^{3} - 3 x^{2} + 2 = m$ có nhiều nghiệm thực nhất khi và chỉ khi -2 < m < 2.

Chọn C.

Câu 9:

Hình vẽ bên là đồ thị của hàm số y= x³-3x-1. Tất cả các giá trị thực của m để phương trình $|x^{3} - 3 x - 1| = m$ có 3 nghiệm đôi một khác nhau là

A. m= 1

B. m> 1.

C. 3< m.

D. m= 0 hoặc m= 3

Xem đáp án

+ Cách vẽ đồ thị hàm số y = |x³- 3x - 1| từ đồ thị hàm số y = x³- 3x - 1 (C) .

+ Giữ nguyên phần đồ thị (C) phía trên trục hoành.

+ Lấy đối xứng phần đồ thị (C) phía dưới trục hoành qua trục hoành và bỏ phần đồ thị phía dưới trụ hoành.

+ Hợp hai phần đồ thị trên ta được đồ thị hàm số y = |x³- 3x - 1|

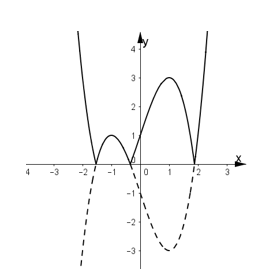
+ Để phương trình |x³- 3x - 1| = m có 3 nghiệm đôi một khác nhau thì đường thẳng y = m cắt đồ thị hàm số tại 3 điểm phân biệt

<=> m = 0 hoặc m = 3

Chọn D.

Câu 10:

Tìm tất cả các giá trị thực k đề phương trình $|- 2 x^{3} - \frac{3}{2} x^{2} + 3 x + \frac{1}{2}|$ = $|\frac{k}{2} - 1|$ có đúng 4 nghiệm phân biệt.

A.k> 6

B. 1< k< 2

C. -2< k< 6

D. k $\in (- 2; - \frac{3}{4}) \cup (\frac{19}{4}; 6)$

Xem đáp án

+ Đặt $f (x) = - 2 x^{3} - \frac{3}{2} x^{2} + 3 x + \frac{1}{2}$

+ Đạo hàm f’(x) = -6x²-3x+ 3 và f’(x) = 0 khi x= -1 hoặc x= 1/2

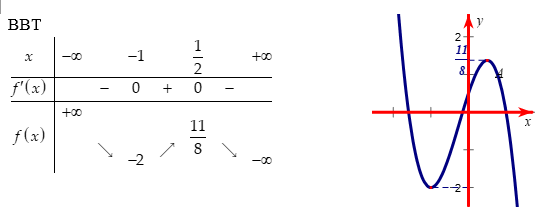
+ Suy ra đồ thị của hàm trị tuyệt đối y = $|- 2 x^{3} - \frac{3}{2} x^{2} + 3 x + \frac{1}{2}|$ bằng cách lấy đối xứng qua trục Ox

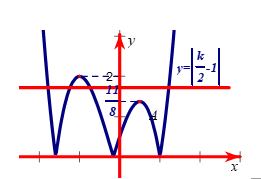
Vậy để PT có đúng 4 nghiệm phân biệt

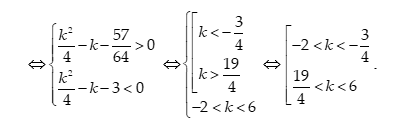
$\leftrightarrow \frac{11}{8} < |\frac{k}{2} - 1| < 2 \leftrightarrow \frac{121}{64} < \frac{k^{2}}{4} - k + 1 < 4$

Chọn D

Câu 11:

Cho hàm số f(x) = $\frac{x - m^{2} + m}{x + 1}$ với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2.

A. m= 1

B. m= -2

C. m= -1

D. m= -1 hoặc m= 2

Xem đáp án

Đạo hàm f'(x) = $\frac{m^{2} - m + 1}{{(x + 1)}^{2}}$ > 0, $\forall x \in [0; 1]$

Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m²+m

Theo bài ta có:

-m²+ m= -2 nên m= -1 hoặc m= 2.

Chọn D.

Câu 12:

Tìm tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = $|x^{2} - 2 x + m|$ trên đoạn [-1; 2] bằng 5.

A. -4

B. 2

C. 0

D . -2

Xem đáp án

+ Xét hàm số f(x) =x²- 2x trên đoạn [ -1; 2],

+ ta có đạo hàm f’(x) = 2( x-1) và f’( x) =0 khi x= 1

Vậy:

TH1: Với $\underset{[- 1, 2]}{m a x} = | m - 1 |$ ,

ta có $\{\begin{matrix} |m - 1| \geq |m + 3| \\ | m - 1 | \geq | m | \\ | m - 1 | = 5 \end{matrix}$

$\leftrightarrow \{\begin{matrix} | m - 1 | \geq |m + 3| \\ | m - 1 | \geq | m | \\ m = - 4 \lor m = 6 \end{matrix}$ $\leftrightarrow m = - 4$

TH2: Với

$\underset{[- 1, 2]}{m a x} y = | m + 3 | \leftrightarrow \{\begin{matrix} | m + 3 | \geq | m - 1 | \\ | m + 3 | \geq | m | \\ | m + 3 | = 5 \end{matrix}$

$\leftrightarrow \{\begin{cases} \begin{matrix} | m + 3 | \geq | | m - 1 | \\ | m + 3 | \geq | m | \\ m = 2 \lor m = - 8 \end{matrix} \end{cases}$ $\leftrightarrow m = 2$

TH3: Với

$\underset{[- 1, 2]}{m a x} y = | m | \leftrightarrow \{\begin{cases} \begin{matrix} | m | \geq | m - 1 | \\ | m | \geq | m + 3 | \\ | m | = 5 \end{matrix} \leftrightarrow \{\begin{cases} \begin{matrix} | m | \geq | m - 1 | \\ | m | \geq | m + 3 | \\ m = 5 \lor m = - 5 \end{matrix} \end{cases} \end{cases}$

( vô nghiệm)

Chọn D.

Câu 13:

Cho hàm số y = $\frac{x + m}{x + 1}$ . Với tham số m bằng bao nhiêu thì thỏa mãn $\underset{[1; 2]}{m i n} y + \underset{[1; 2]}{m a x y} = \frac{16}{3}$ trên đoạn [1; 2].

A. m=0

B. m= 2

C. m= 4

D. m= 5

Xem đáp án

+ Đạo hàm f'(x) = $\frac{1 - m}{{(x + 1)}^{2}}$ .

+ Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m≠ 1.

+ Khi đó ta có :

$\underset{[1; 2]}{m i n y} + \underset{[1; 2]}{m a x} y = f (1) + f (2) \leftrightarrow \frac{m + 1}{2} + \frac{m + 2}{3} = \frac{16}{3} \leftrightarrow \frac{5 m}{6} = \frac{25}{6} \leftrightarrow m = 5$

Chọn D.

Câu 14:

Cho hàm số f(x) = $\frac{2 \sqrt{x} + m}{\sqrt{x + 1}}$ với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.

A. 1<m< 3

B. m $\in (1; 3 \sqrt{5} - 4)$

C. m $\in (1; \sqrt{5})$

D. 1<m≤ 4

Xem đáp án

+ Đạo hàm f'(x) = $\frac{2 - m \sqrt{x}}{2 (x + 1) \sqrt{x (x + 1)}}$

f'(x) = 0 $\Rightarrow \sqrt{x} = \frac{2}{m} \leftrightarrow x = \frac{m^{2}}{4} \in [0; 4]$ , $\forall m > 1$

+ Lập bảng biến thiên, ta kết luận được

$\underset{[0; 4]}{m a x} f (x) = f (\frac{4}{m^{2}}) = \sqrt{m^{2} + 4}$

+ Vậy ta cần có $\sqrt{m^{2} + 4} < 3$

$\leftrightarrow m < \sqrt{5}$ $\overset{m > 1}{\to} m \in (1; \sqrt{5})$

Chọn C.

Câu 15:

Cho hàm số y = x³- 3x + 1 . Tìm tìm tập hợp tất cả giá trị m> 0 , để giá trị nhỏ nhất của hàm số trên D = [m + 1; m + 2] luôn bé hơn 3 là:

A. (0; 1)

B. ( $\frac{1}{2}$ ; 1)

C. (2; 3)

D. (0; 2)

Xem đáp án

+ Ta có đạo hàm: y = 3x²- 3 và y’ =0 khi và chỉ khi x = 1 hoặc x = -1 .

+ Hàm số đồng biến trên khoảng (1; +∞) .

+ Trên D= [m + 1; m + 2], với m > 0 ,

ta có : $\underset{[m + 1; m + 2]}{M i n} y = {(m + 1)}^{3} - 3 (m + 1) + 1$

Ycbt min y < 3 hay m³+ 3m²- 4 < 0

Suy ra ( m - 1)(m + 2) ²) < 0

Khi đó: m < 1 và m ≠ - 2

+ Kết hợp điều kiện . Suy ra: 0 < m < 1.

Chọn A.

Câu 16:

Cho hàm số y = $\frac{x + m}{x - 1}$ với tham số m bằng bao nhiêu thì $\underset{[2; 4]}{m i n} y = 3$

A. m= 1

B. m= 3

C. m= 5

D. m= -1

Xem đáp án

+ Đạo hàm f'(x) = $- \frac{m + 1}{{(x - 1)}^{2}}$

TH1. Với m> -1 suy ra f’(x) <0 mọi x≠ 1 nên hàm số f(x) nghịch biến trên mỗi khoảng xác định.

Khi đó $\underset{[2; 4]}{m i n} y = f (4) = \frac{m + 4}{3} = 3 \leftrightarrow m = 5$ (chọn).

TH2. Với m< -1 suy ra f”(x) > 0 mọi x≠1 nên hàm số f( x) đồng biến trên mỗi khoảng xác định.

Khi đó $\underset{[2; 4]}{m i n} y = f (2) = m + 2 = 3 \leftrightarrow$ m = 1 (loại).

Chọn C.

Câu 17:

Tìm tất cả các giá trị thực của tham số m để hàm số y = $\frac{x^{2} + m x + 1}{x + m}$ liên tục và đạt cực tiểu trên [0;2] tại một điểm 0 < x₀< 2.

A. 0 < m < 1

B. m < 0

C.m > 1

D. -1 < m < 0

Xem đáp án

Điều kiện : x ≠ -m.

+ Ta có: $y' = \frac{x^{2} + 2 m x + m^{2} - 1}{{(x + m)}^{2}} = \frac{{(x + m)}^{2} - 1}{{(x + m)}^{2}}$

$y' = 0 \leftrightarrow {(x + m)}^{2} = 1 \leftrightarrow x = 1 - m > - m \lor x = - 1 - m < - m$

+ Do hệ số x² là số dương và theo yêu cầu đề bài ta có bảng biến thiên như sau:

+ Hàm số đạt cực tiểu tại x₀= 1 - m ∈ (0; 2) nên 0 < -m + 1 < 2

Hay -1 < m < 1.

+ Kết hợp điều kiện để hàm số liên tục trên [0; 2] thì

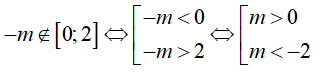
Ta được 0 < m < 1

Chọn A

Câu 18:

Tìm m để bất phương trình x²- 5mx + 9 ≥ 0 có nghiệm x ?

A. m ≤ 2

B. m ≤ 1

C. m ≥ 2

D. Đáp án khác

Xem đáp án

+ Với x $\in [1; 9] p t \leftrightarrow \frac{x^{2} + 9}{x} \geq 5 m$

Xét f(x) = $\frac{x^{2} + 9}{x}; f' (x) = \frac{x^{2} - 9}{x^{2}}$

+Suy ra $\{\begin{cases} f' (x) = 0 \\ x \in (1; 9) \end{cases} \leftrightarrow x = 3$

Ycbt $\underset{[1; 9]}{M a x} f (x) \geq 5 m \leftrightarrow m \leq 2$

Chọn A.

Câu 19:

Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y để dịnh tích hình thang EFGH đạt giá trị nhỏ nhất.

A. $2 + \sqrt{3}$

B. $3 \sqrt{2}$

C. $2 \sqrt{2}$

D. Tất cả sai

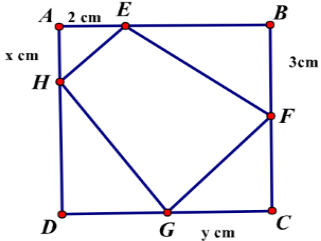
Xem đáp án

Ta có S_EFGH nhỏ nhất $\leftrightarrow S = S_{A E H} + S_{C G F} + S_{D G H}$ lớn nhất

Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)

Mặt khác ∆ AEH đồng dạng ∆CGF nên $\frac{A E}{C G} = \frac{A H}{C F} \Rightarrow x y = 6$

Từ (1) và (2) suy ra 2S = $42 - (4 x - \frac{18}{x})$

Ta có 2S lớn nhất khi và chỉ khi $4 x - \frac{18}{x}$ nhỏ nhất.

Biểu thức nhỏ nhất $4 x - \frac{18}{x}$ nhỏ nhất $\leftrightarrow 4 x = \frac{18}{x} \Rightarrow x = \frac{3 \sqrt{2}}{2} \Rightarrow y = 2 \sqrt{2}$

Vậy x+y = $\frac{3 \sqrt{2}}{2} + 2 \sqrt{2}$

Chọn D.

Câu 20:

Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn gần với giá trị nào nhất để ít tốn vật liệu nhất?

A. 10, 5

B. 10,6

C. 10, 7

D. 10, 8

Xem đáp án

Để ít tốn vật liệu nhất thì diện tích toàn phần bồn nước phải nhỏ nhất.

Tức là S_tp= 2πR²+ 2πRh nhỏ nhất ( với R là bán kính đường tròn đáy)

Thể tích bồn nước V $= π R^{2} h = 1000 \Rightarrow R = \sqrt{\frac{1000}{π h}}$

Khi đó :

Sử dụng bảng biến thiên, ta tìm được S_tp nhỏ nhất khi

$h = \sqrt[3]{\frac{4000}{π}}$

Chọn D.